概述¶
Alphalens旨在帮助分析"阿尔法因子"——这些数据转换用于预测金融工具的未来价格走势。阿尔法因子以每日每个资产对应单一数值的形式呈现。这些数值的维度并不一定重要。我们通过比较每日因子值之间的相对关系来评估阿尔法因子。
需要重点区分alpha因子与交易算法的差异。交易算法会使用一个或多个alpha因子来生成交易信号,其涵盖执行与风控约束——核心是将预测转化为实际收益。而alpha因子则纯粹聚焦于预测本身。这种范畴差异导致评估alpha因子与交易算法的方法论存在本质不同。
Alphalens不包含对交易成本、容量或投资组合构建等内容的分析。对于更关注具体实施分析的读者,我们推荐查看pyfolio,这是一个专门用于评估交易算法的库。
导入与设置¶
[1]:
import warnings
warnings.filterwarnings('ignore')
[3]:
import pandas as pd
import alphalens
import seaborn as sns
[4]:
%matplotlib inline
sns.set_style('white')
加载与转换数据¶
[5]:
ticker_sector = {
"ACN": 0, "ATVI": 0, "ADBE": 0, "AMD": 0, "AKAM": 0, "ADS": 0, "GOOGL": 0, "GOOG": 0,
"APH": 0, "ADI": 0, "ANSS": 0, "AAPL": 0, "AMAT": 0, "ADSK": 0, "ADP": 0, "AVGO": 0,
"AMG": 1, "AFL": 1, "ALL": 1, "AXP": 1, "AIG": 1, "AMP": 1, "AON": 1, "AJG": 1, "AIZ": 1, "BAC": 1,
"BK": 1, "BBT": 1, "BRK.B": 1, "BLK": 1, "HRB": 1, "BHF": 1, "COF": 1, "CBOE": 1, "SCHW": 1, "CB": 1,
"ABT": 2, "ABBV": 2, "AET": 2, "A": 2, "ALXN": 2, "ALGN": 2, "AGN": 2, "ABC": 2, "AMGN": 2, "ANTM": 2,
"BCR": 2, "BAX": 2, "BDX": 2, "BIIB": 2, "BSX": 2, "BMY": 2, "CAH": 2, "CELG": 2, "CNC": 2, "CERN": 2,
"MMM": 3, "AYI": 3, "ALK": 3, "ALLE": 3, "AAL": 3, "AME": 3, "AOS": 3, "ARNC": 3, "BA": 3, "CHRW": 3,
"CAT": 3, "CTAS": 3, "CSX": 3, "CMI": 3, "DE": 3, "DAL": 3, "DOV": 3, "ETN": 3, "EMR": 3, "EFX": 3,
"AES": 4, "LNT": 4, "AEE": 4, "AEP": 4, "AWK": 4, "CNP": 4, "CMS": 4, "ED": 4, "D": 4, "DTE": 4,
"DUK": 4, "EIX": 4, "ETR": 4, "ES": 4, "EXC": 4, "FE": 4, "NEE": 4, "NI": 4, "NRG": 4, "PCG": 4,
"ARE": 5, "AMT": 5, "AIV": 5, "AVB": 5, "BXP": 5, "CBG": 5, "CCI": 5, "DLR": 5, "DRE": 5,
"EQIX": 5, "EQR": 5, "ESS": 5, "EXR": 5, "FRT": 5, "GGP": 5, "HCP": 5, "HST": 5, "IRM": 5, "KIM": 5,
"APD": 6, "ALB": 6, "AVY": 6, "BLL": 6, "CF": 6, "DWDP": 6, "EMN": 6, "ECL": 6, "FMC": 6, "FCX": 6,
"IP": 6, "IFF": 6, "LYB": 6, "MLM": 6, "MON": 6, "MOS": 6, "NEM": 6, "NUE": 6, "PKG": 6, "PPG": 6,
"T": 7, "CTL": 7, "VZ": 7,
"MO": 8, "ADM": 8, "BF.B": 8, "CPB": 8, "CHD": 8, "CLX": 8, "KO": 8, "CL": 8, "CAG": 8,
"STZ": 8, "COST": 8, "COTY": 8, "CVS": 8, "DPS": 8, "EL": 8, "GIS": 8, "HSY": 8, "HRL": 8,
"AAP": 9, "AMZN": 9, "APTV": 9, "AZO": 9, "BBY": 9, "BWA": 9, "KMX": 9, "CCL": 9,
"APC": 10, "ANDV": 10, "APA": 10, "BHGE": 10, "COG": 10, "CHK": 10, "CVX": 10, "XEC": 10, "CXO": 10,
"COP": 10, "DVN": 10, "EOG": 10, "EQT": 10, "XOM": 10, "HAL": 10, "HP": 10, "HES": 10, "KMI": 10
}
详情请参阅yfinance。
[6]:
import yfinance as yf
import pandas_datareader.data as web
yf.pdr_override()
tickers = list(ticker_sector.keys())
df = web.get_data_yahoo(tickers, start='2014-12-01', end='2017-01-01')
df.index = pd.to_datetime(df.index, utc=True)
[*********************100%***********************] 182 of 182 completed
19 Failed downloads:
- DPS: No data found for this date range, symbol may be delisted
- CBG: No data found for this date range, symbol may be delisted
- CHK: Data doesn't exist for startDate = 1417413600, endDate = 1483250400
- CELG: No data found, symbol may be delisted
- ARNC: Data doesn't exist for startDate = 1417413600, endDate = 1483250400
- BRK.B: No data found, symbol may be delisted
- AGN: No data found, symbol may be delisted
- CXO: No data found, symbol may be delisted
- MON: Data doesn't exist for startDate = 1417413600, endDate = 1483250400
- BCR: No data found for this date range, symbol may be delisted
- DWDP: No data found, symbol may be delisted
- CTL: No data found, symbol may be delisted
- APC: No data found, symbol may be delisted
- GGP: No data found for this date range, symbol may be delisted
- HCP: No data found, symbol may be delisted
- BHF: Data doesn't exist for startDate = 1417413600, endDate = 1483250400
- BHGE: No data found, symbol may be delisted
- BF.B: No data found for this date range, symbol may be delisted
- BBT: No data found, symbol may be delisted
[7]:
df = df.stack()
df.index.names = ['date', 'asset']
df.info()
<class 'pandas.core.frame.DataFrame'>
MultiIndex: 85738 entries, (Timestamp('2014-12-01 00:00:00+0000', tz='UTC'), 'A') to (Timestamp('2016-12-30 00:00:00+0000', tz='UTC'), 'XOM')
Data columns (total 6 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Adj Close 85738 non-null float64
1 Close 85738 non-null float64
2 High 85738 non-null float64
3 Low 85738 non-null float64
4 Open 85738 non-null float64
5 Volume 85738 non-null float64
dtypes: float64(6)
memory usage: 4.3+ MB
计算因子¶
出于演示目的,我们将创建一个预测因子。为了"作弊",我们会参考未来价格,确保能准确筛选出表现优异的高排名股票,反之亦然。
[8]:
lookahead_bias_days = 5
predictive_factor = df.loc[:, 'Open'].unstack('asset')
predictive_factor = predictive_factor.pct_change(lookahead_bias_days)
# introduce look-ahead bias and make the factor predictive
predictive_factor = predictive_factor.shift(-lookahead_bias_days)
predictive_factor = predictive_factor.stack()
[9]:
predictive_factor.head()
[9]:
date asset
2014-12-01 00:00:00+00:00 A -0.010775
AAL 0.029388
AAP 0.057920
AAPL -0.039643
ABBV 0.010567
dtype: float64
获取价格信息¶
传递给alphalens的定价数据应包含资产的入场价格,因此必须反映在给定时间戳观察到因子值后的下一个可用价格。这些价格不得用于计算该时间点的因子值。务必反复检查,确保您的研究没有引入前瞻性偏差。
价格数据还必须包含资产的退出价格,对于周期1将使用下一个时间戳的价格,对于周期2将使用2个时间步长后的价格,以此类推。
对于计算因子时使用的时间频率没有限制/假设,对于交易因子的具体时间也没有限制(开盘交易、收盘交易或日内交易),唯一的要求是根据上述规则确保因子和价格数据框正确对齐。
在我们的示例中,每天交易开始前,我们会观察昨日的因子值。传递给alphalens的价格是该因子观测后的下一个可用价格:即作为资产入场价的每日开盘价。同时,由于我们没有添加额外价格数据,资产出场价将是后续交易日的开盘价(具体天数取决于'periods'参数)。因此Alphalens计算的收益将基于资产的开盘价。
[10]:
pricing = df.loc[:, 'Open'].iloc[1:].unstack('asset')
pricing.head()
[10]:
| 资产 | AAL | AAP | AAPL | ABBV | ABC | ABT | ACN | ADBE | ADI | ADM | ... | PCG | PKG | PPG | SCHW | STZ | T | VZ | XEC | XOM | A |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 日期 | |||||||||||||||||||||
| 2014-12-01 00:00:00+00:00 | 49.000000 | 146.410004 | 29.702499 | 69.080002 | 90.639999 | 44.270000 | 85.879997 | 73.639999 | 54.480000 | 52.660000 | ... | 50.209999 | 74.250000 | 108.730003 | 28.080000 | 95.820000 | 35.279999 | 50.680000 | 103.980003 | 90.360001 | NaN |
| 2014-12-02 00:00:00+00:00 | 48.119999 | 146.710007 | 28.375000 | 68.879997 | 90.930000 | 44.680000 | 85.849998 | 74.000000 | 54.540001 | 52.740002 | ... | 50.689999 | 73.209999 | 110.605003 | 27.860001 | 94.930000 | 34.889999 | 49.799999 | 102.790001 | 92.320000 | 41.599998 |
| 2014-12-03 00:00:00+00:00 | 47.740002 | 148.440002 | 28.937500 | 69.169998 | 91.989998 | 45.220001 | 86.400002 | 73.639999 | 54.950001 | 53.330002 | ... | 51.500000 | 74.779999 | 109.800003 | 28.200001 | 94.260002 | 34.250000 | 49.020000 | 103.809998 | 94.669998 | 41.980000 |
| 2014-12-04 00:00:00+00:00 | 49.599998 | 152.419998 | 28.942499 | 68.349998 | 91.870003 | 45.660000 | 86.410004 | 73.089996 | 56.459999 | 53.270000 | ... | 50.910000 | 76.760002 | 111.555000 | 28.940001 | 94.010002 | 34.080002 | 48.730000 | 105.550003 | 94.129997 | 42.150002 |
| 2014-12-05 00:00:00+00:00 | 50.090000 | 154.210007 | 28.997499 | 69.519997 | 92.379997 | 45.430000 | 86.309998 | 73.160004 | 56.750000 | 52.750000 | ... | 49.860001 | 77.790001 | 111.949997 | 29.770000 | 94.250000 | 33.880001 | 48.680000 | 106.860001 | 93.949997 | 42.230000 |
5行 × 163列
通常,我们希望了解因子在不同分组(行业、产业、国家等)中的表现,在这个示例中我们将使用行业分类。要生成行业层面的细分分析,您需要向alphalens提供每个交易品种的行业映射关系。
如果您希望为每个交易日的每个股票提供行业分类映射,这种映射可以采用多级索引序列的形式(与因子值具有相同的日期/股票索引)。
如需使用固定行业映射关系,您可以将股票代码与行业的映射以字典形式传入。
如果您的行业分类以代码形式呈现(如本教程所示),您也可以向alphalens传递一个行业名称字典来替代行业代码。
[11]:
sector_names = {
0: "information_technology",
1: "financials",
2: "health_care",
3: "industrials",
4: "utilities",
5: "real_estate",
6: "materials",
7: "telecommunication_services",
8: "consumer_staples",
9: "consumer_discretionary",
10: "energy"
}
格式化分析报告输入数据¶
Alphalens 包含一个便捷的数据格式化函数,可将您的因子和定价数据转换为适合tear sheet函数使用的标准输入格式。
[12]:
factor_data = alphalens.utils.get_clean_factor_and_forward_returns(predictive_factor,
pricing,
quantiles=5,
bins=None,
groupby=ticker_sector,
groupby_labels=sector_names)
Dropped 1.0% entries from factor data: 1.0% in forward returns computation and 0.0% in binning phase (set max_loss=0 to see potentially suppressed Exceptions).
max_loss is 35.0%, not exceeded: OK!
该函数用于告知用户在格式化输入数据后丢弃了多少数据。因子数据可能因自身存在缺陷(如NaN值)、未提供足够的价格数据来计算所有因子值的远期收益,或无法进行分箱处理而被部分丢弃。用户可以通过'max_loss'参数控制允许的最大数据丢失量。
[13]:
factor_data.head()
[13]:
| 1天 | 5天 | 10天 | 因子 | 分组 | 因子分位数 | ||
|---|---|---|---|---|---|---|---|
| 日期 | 资产 | ||||||
| 2014-12-01 00:00:00+00:00 | AAL | -0.017959 | 0.029388 | 0.024694 | 0.029388 | 工业 | 5 |
| AAP | 0.002049 | 0.057920 | 0.104433 | 0.057920 | 可选消费 | 5 | |
| AAPL | -0.044693 | -0.039643 | -0.068260 | -0.039643 | information_technology | 1 | |
| ABBV | -0.002895 | 0.010567 | -0.048205 | 0.010567 | 医疗保健 | 3 | |
| ABC | 0.003199 | 0.015115 | 0.010040 | 0.015115 | health_care | 4 |
您会注意到,我们已经将所有计算所需的信息整合到一个数据框中。变量对应各列,观测值对应每行。
整数列表示时间戳后N天的远期收益率或每日价格变动。例如,AAPL在2014-12-2的1日远期收益率是指2014-12-2的AAPL开盘价与2014-12-3的AAPL开盘价之间的百分比变化。5日远期收益率则是从2014-12-2开盘价到2014-12-9开盘价(5个交易日)的百分比变化除以5。
收益分析¶
收益分析为我们提供了因子价值的原始描述,以实际货币值展示该因子的效力。
评估因子预测能力最基本的方法之一,是观察不同因子分位数的平均收益率。
性能指标与绘图函数¶
[14]:
mean_return_by_q_daily, std_err = alphalens.performance.mean_return_by_quantile(
factor_data, by_date=True)
[15]:
mean_return_by_q_daily.head()
[15]:
| 1天 | 5天 | 10天 | ||
|---|---|---|---|---|
| 因子分位数 | 日期 | |||
| 1 | 2014-12-01 00:00:00+00:00 | -0.011639 | -0.040503 | -0.048165 |
| 2014-12-02 00:00:00+00:00 | -0.001948 | -0.042854 | -0.051933 | |
| 2014-12-03 00:00:00+00:00 | -0.009176 | -0.048059 | -0.047047 | |
| 2014-12-04 00:00:00+00:00 | -0.003707 | -0.048854 | -0.025982 | |
| 2014-12-05 00:00:00+00:00 | -0.014295 | -0.057625 | -0.034734 |
[16]:
mean_return_by_q, std_err_by_q = alphalens.performance.mean_return_by_quantile(
factor_data, by_date=False)
[17]:
mean_return_by_q.head()
[17]:
| 1天 | 5天 | 10天 | |
|---|---|---|---|
| 因子分位数 | |||
| 1 | -0.008624 | -0.041080 | -0.041164 |
| 2 | -0.002719 | -0.013478 | -0.013805 |
| 3 | -0.000089 | -0.000332 | -0.000289 |
| 4 | 0.002760 | 0.012724 | 0.012964 |
| 5 | 0.008672 | 0.042145 | 0.042270 |
[20]:
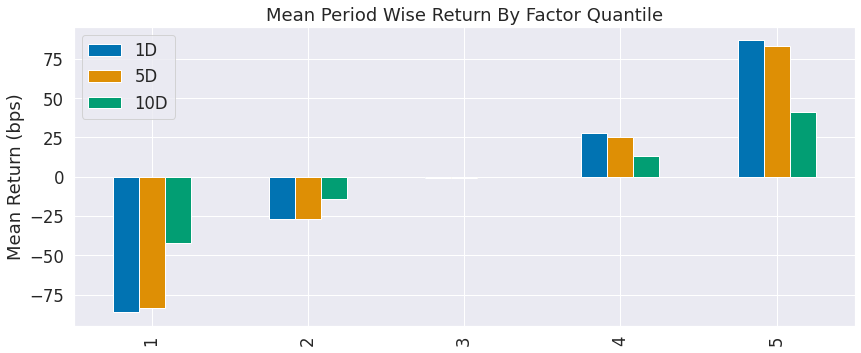
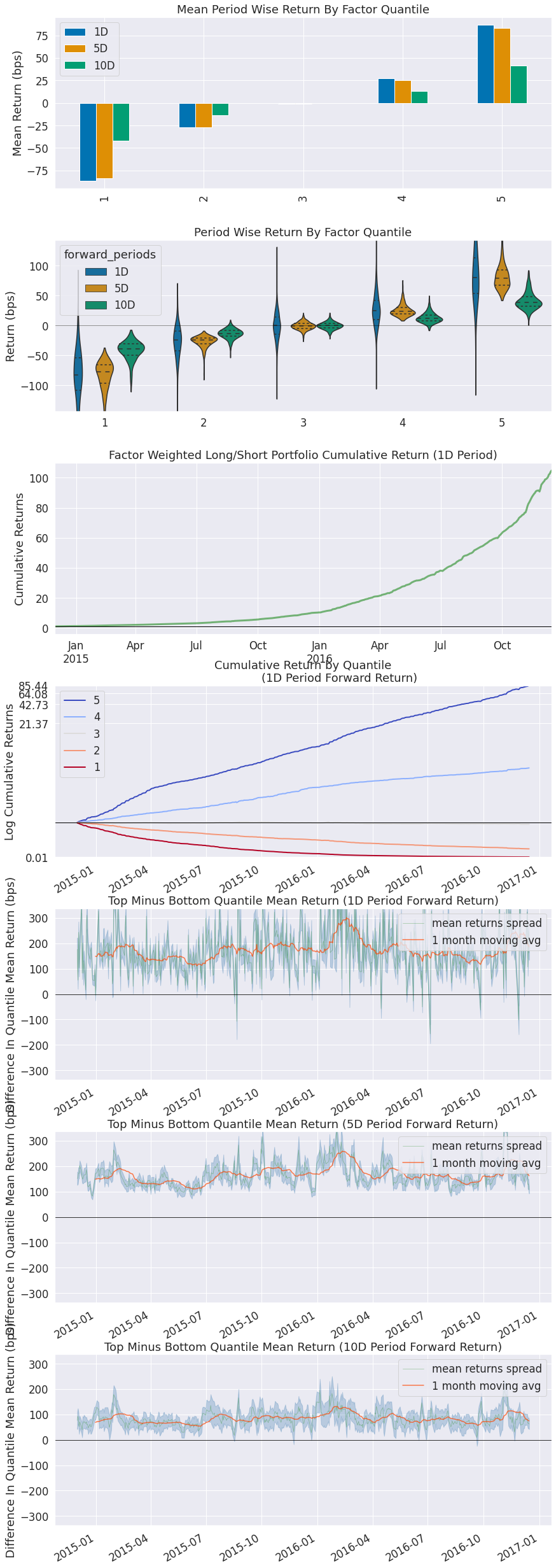
alphalens.plotting.plot_quantile_returns_bar(mean_return_by_q)
sns.despine()
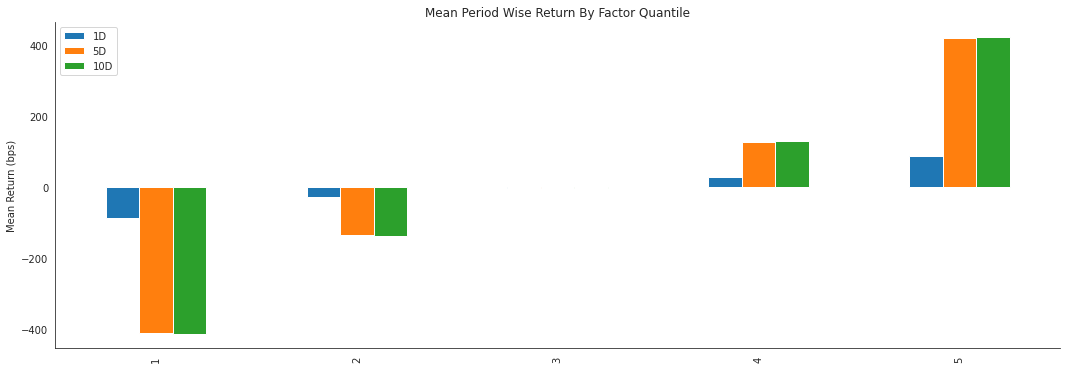
通过观察分位数的平均收益率,我们可以真实了解该因子如何根据信号值区分未来收益。显然,我们希望信号较好的证券能表现出更高的收益。对于一个优质因子,我们预期会在较低分位数看到负值,在较高分位数看到正值。
[21]:
alphalens.plotting.plot_quantile_returns_violin(mean_return_by_q_daily)
sns.despine()

这个小提琴图与之前的类似,但展示了更多关于基础数据的信息。它能更好地呈现数值范围、中位数以及四分位距。图表形状的形成源于对不同数值点上数据概率密度的应用。
[22]:
quant_return_spread, std_err_spread = alphalens.performance.compute_mean_returns_spread(mean_return_by_q_daily,
upper_quant=5,
lower_quant=1,
std_err=std_err)
[24]:
alphalens.plotting.plot_mean_quantile_returns_spread_time_series(
quant_return_spread, std_err_spread);
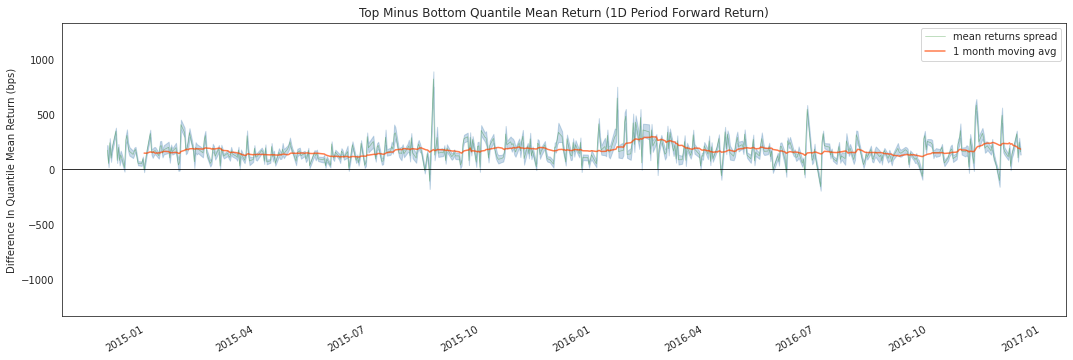
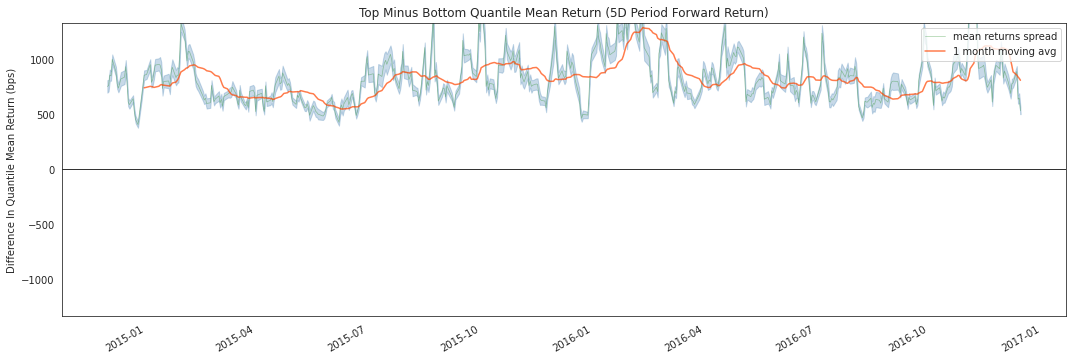
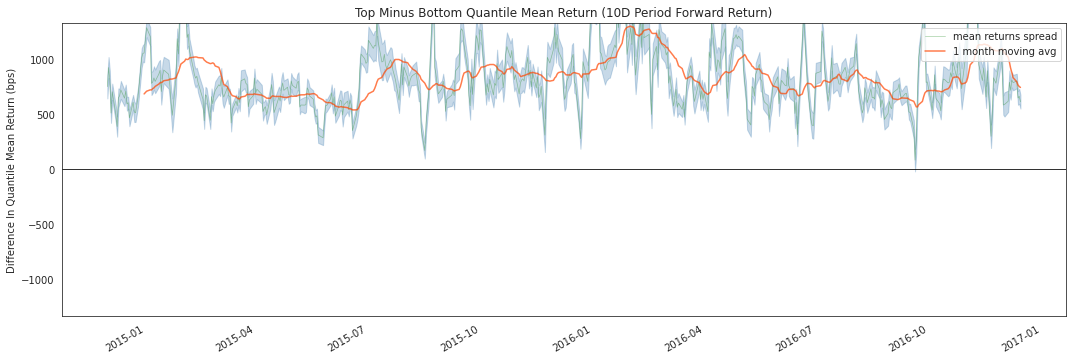
这个滚动远期收益价差图使我们能够观察随时间推移顶部和底部分位数之间的原始价差(以基点计)。绿色线表示收益价差,而橙色线是1个月平均值,用于平滑数据使其更易于可视化。
[25]:
alphalens.plotting.plot_cumulative_returns_by_quantile(
mean_return_by_q_daily, period='1D');
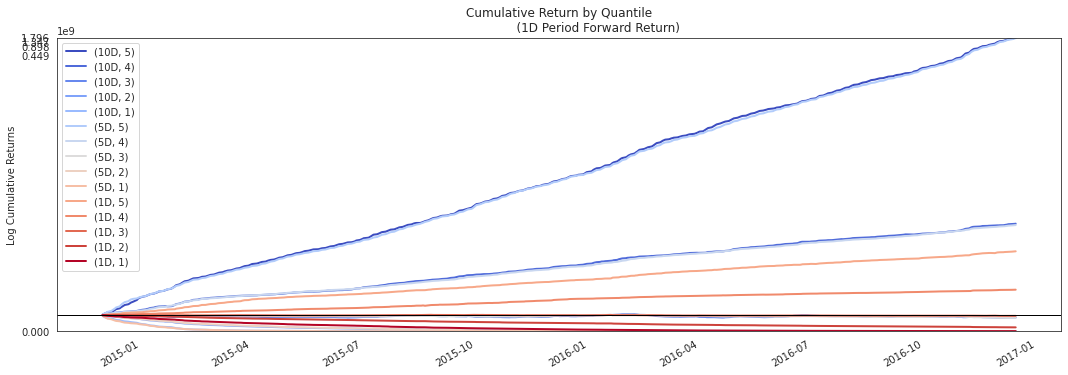
通过观察按因子分位数的累计收益,我们可以直观了解哪些分位数对因子贡献最大以及贡献发生的时间。理想情况下,我们希望看到这些曲线从左侧相同的起点出发,随着时间向右延伸像扇子一样展开,其中较高分位数位于顶部。
[26]:
ls_factor_returns = alphalens.performance.factor_returns(factor_data)
[27]:
ls_factor_returns.head()
[27]:
| 1天 | 5天 | 10天 | |
|---|---|---|---|
| 日期 | |||
| 2014-12-01 00:00:00+00:00 | 0.009314 | 0.042049 | 0.041802 |
| 2014-12-02 00:00:00+00:00 | 0.003506 | 0.040637 | 0.046887 |
| 2014-12-03 00:00:00+00:00 | 0.012037 | 0.043812 | 0.041752 |
| 2014-12-04 00:00:00+00:00 | 0.004942 | 0.040428 | 0.028340 |
| 2014-12-05 00:00:00+00:00 | 0.009555 | 0.046433 | 0.031056 |
[28]:
alphalens.plotting.plot_cumulative_returns(
ls_factor_returns['1D'], period='1D');
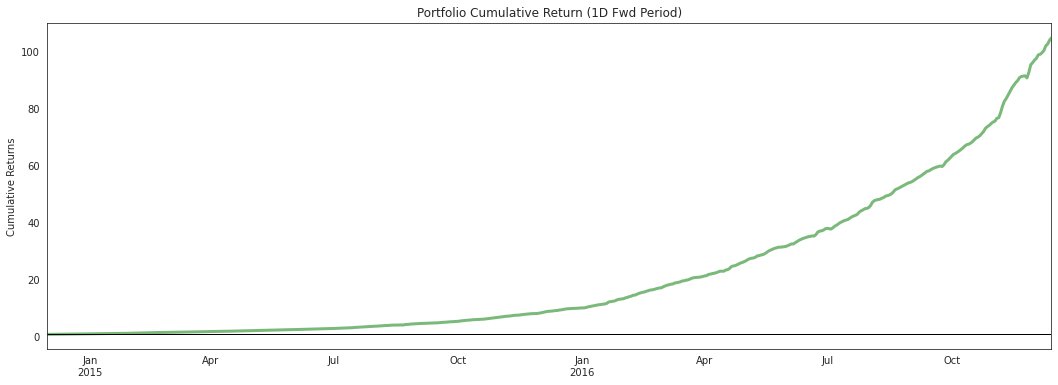
虽然观察分位数很重要,但我们也必须整体考察因子收益。累积因子多空收益图让我们能够观察整个因子随时间推移的综合效应。
[29]:
alpha_beta = alphalens.performance.factor_alpha_beta(factor_data)
[30]:
alpha_beta
[30]:
| 1天 | 5天 | 10天 | |
|---|---|---|---|
| 年化阿尔法 | 8.656010 | 7.927868 | 1.985069 |
| beta | 0.093763 | 0.079954 | 0.061756 |
因子收益分析中非常重要的一部分是确定alpha值及其显著性。这里我们展示了年化alpha和beta值。
信息分析¶
信息分析是一种评估因子预测价值的方法,能够避免交易成本带来的混杂影响。我们主要通过信息系数(IC)来进行这项分析。
来自维基百科...
信息系数(IC)是衡量预测值优劣的指标。在金融领域,信息系数被用作评估金融分析师预测能力的绩效指标。信息系数与相关性类似,可以衡量两个随机变量之间的线性关系,例如预测股票收益与实际实现的收益。信息系数的取值范围为0到1,0表示预测值与实际值之间不存在线性关系(预测能力差),1表示完全线性关系(预测能力强)。
性能指标与绘图函数¶
[31]:
ic = alphalens.performance.factor_information_coefficient(factor_data)
[32]:
ic.head()
[32]:
| 1天 | 5天 | 10天 | |
|---|---|---|---|
| 日期 | |||
| 2014-12-01 00:00:00+00:00 | 0.355752 | 1.0 | 0.561977 |
| 2014-12-02 00:00:00+00:00 | 0.230225 | 1.0 | 0.718246 |
| 2014-12-03 00:00:00+00:00 | 0.485738 | 1.0 | 0.716855 |
| 2014-12-04 00:00:00+00:00 | 0.306327 | 1.0 | 0.609102 |
| 2014-12-05 00:00:00+00:00 | 0.485616 | 1.0 | 0.728141 |
[34]:
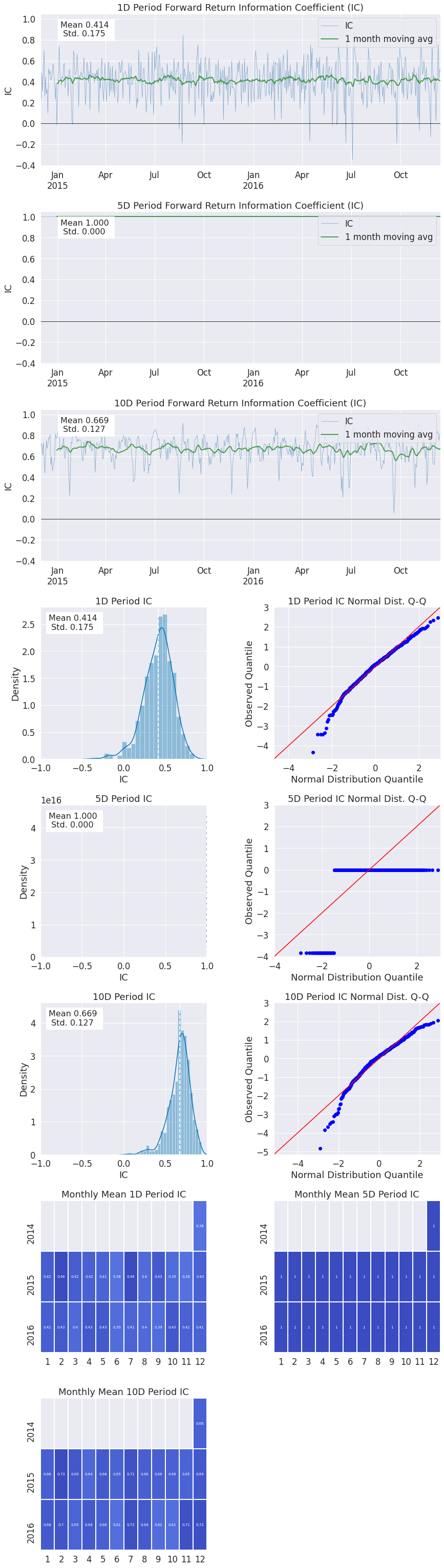
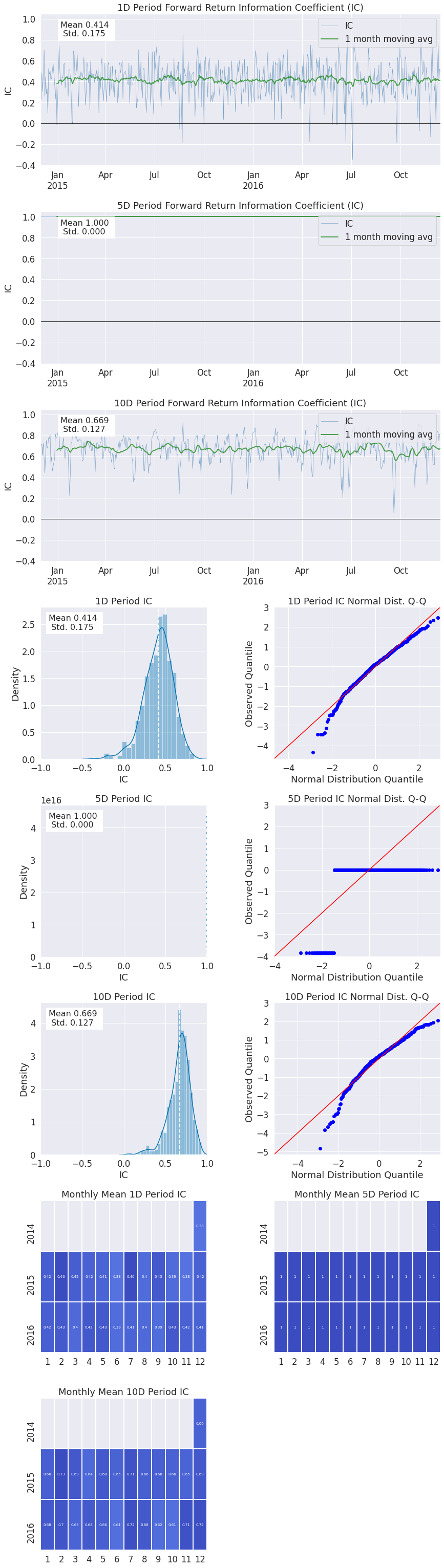
alphalens.plotting.plot_ic_ts(ic);
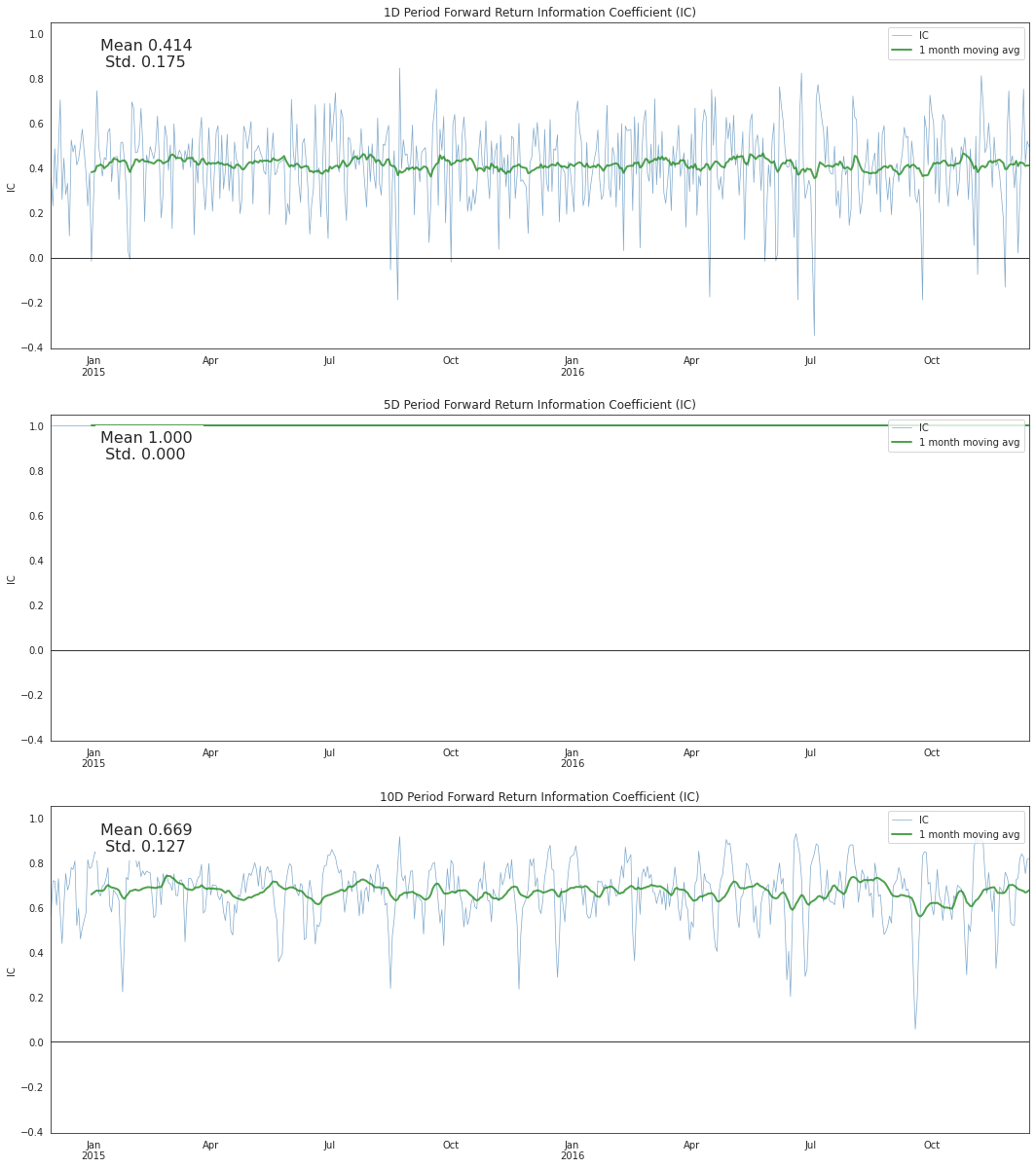
通过每日观察信息系数(IC),我们可以从理论上了解因子随时间变化的预测能力。我们希望平均IC值较高,同时其标准差(即波动性)较低。我们的目标是找到具有持续预测能力的因子。
[35]:
alphalens.plotting.plot_ic_hist(ic);
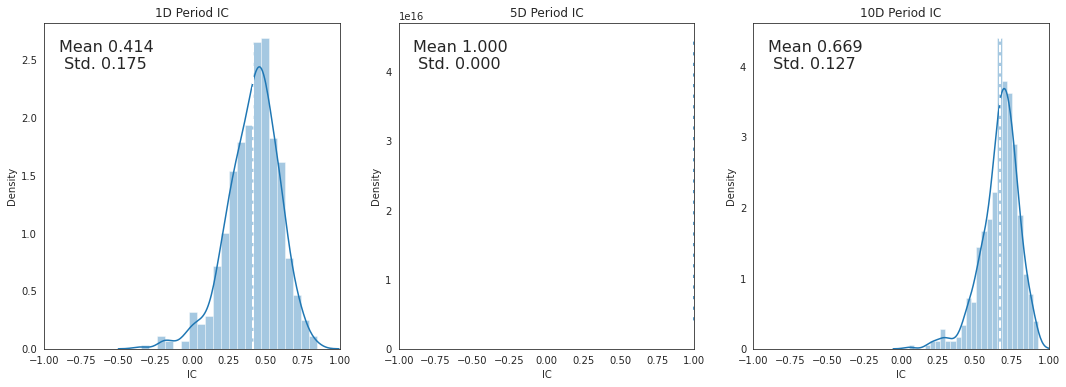
观察每日IC值的直方图可以显示该因子在大多数时间的行为表现,预测可能的IC值分布区间,同时也能让我们判断该因子是否存在厚尾特征。
[36]:
alphalens.plotting.plot_ic_qq(ic);
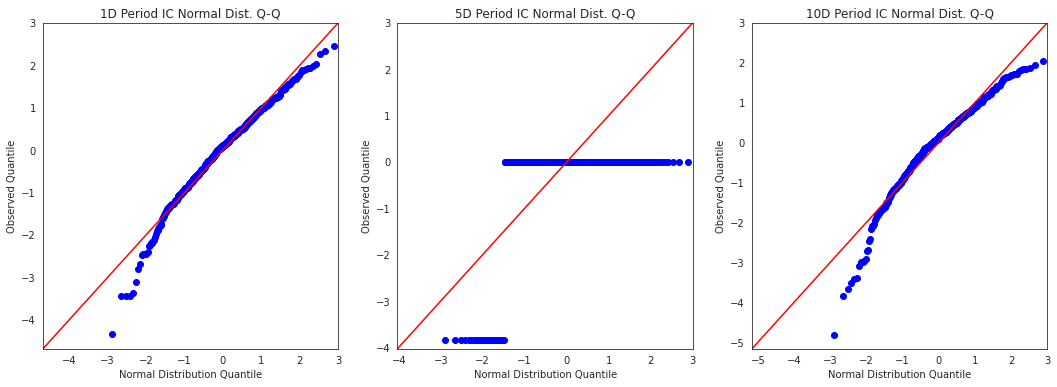
这些Q-Q图展示了IC值分布与正态分布在形状上的差异。这对于观察分布中最极端的值如何影响预测能力特别有帮助。
[37]:
mean_monthly_ic = alphalens.performance.mean_information_coefficient(
factor_data, by_time='M')
[38]:
mean_monthly_ic.head()
[38]:
| 1天 | 5天 | 10天 | |
|---|---|---|---|
| 日期 | |||
| 2014-12-31 00:00:00+00:00 | 0.380726 | 1.0 | 0.657422 |
| 2015-01-31 00:00:00+00:00 | 0.424420 | 1.0 | 0.663536 |
| 2015-02-28 00:00:00+00:00 | 0.462670 | 1.0 | 0.729582 |
| 2015-03-31 00:00:00+00:00 | 0.423443 | 1.0 | 0.685343 |
| 2015-04-30 00:00:00+00:00 | 0.417112 | 1.0 | 0.638436 |
[39]:
alphalens.plotting.plot_monthly_ic_heatmap(mean_monthly_ic);

通过以热力图形式展示IC数据,我们可以了解该因子的稳定性,以及它在不同市场环境/季节中的表现情况。
信息分析报表¶
我们可以一起查看所有信息分析计算结果。
[40]:
alphalens.tears.create_information_tear_sheet(factor_data);
Information Analysis
| 1天 | 5天 | 10天 | |
|---|---|---|---|
| IC均值 | 0.414 | 1.000000e+00 | 0.669 |
| IC标准差 | 0.175 | 0.000000e+00 | 0.127 |
| 风险调整后IC值 | 2.361 | 3.455090e+16 | 5.273 |
| t统计量(IC) | 53.633 | 7.848456e+17 | 119.777 |
| p值(IC) | 0.000 | 0.000000e+00 | 0.000 |
| IC偏度 | -0.673 | -3.840000e+00 | -1.034 |
| IC峰度 | 1.145 | 1.174300e+01 | 2.099 |
<Figure size 432x288 with 0 Axes>
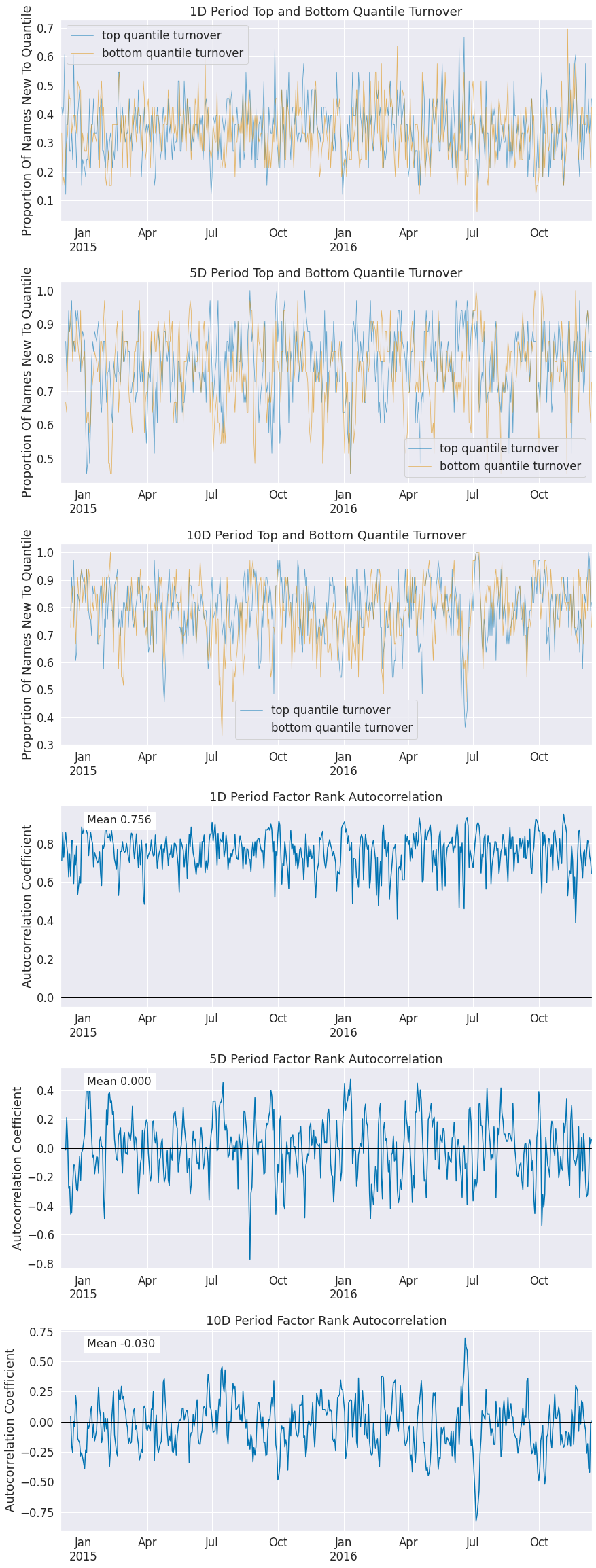
换手率分析¶
换手率分析让我们了解一个因子的构成特性及其变化情况。
性能指标与绘图函数¶
[41]:
quantile_factor = factor_data['factor_quantile']
turnover_period = 1
[42]:
quantile_turnover = pd.concat([alphalens.performance.quantile_turnover(quantile_factor, q, turnover_period)
for q in range(1, int(quantile_factor.max()) + 1)], axis=1)
[43]:
quantile_turnover.head()
[43]:
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 日期 | |||||
| 2014-12-01 00:00:00+00:00 | NaN | NaN | NaN | NaN | NaN |
| 2014-12-02 00:00:00+00:00 | 0.333333 | 0.62500 | 0.666667 | 0.50000 | 0.424242 |
| 2014-12-03 00:00:00+00:00 | 0.151515 | 0.37500 | 0.545455 | 0.53125 | 0.393939 |
| 2014-12-04 00:00:00+00:00 | 0.181818 | 0.53125 | 0.757576 | 0.68750 | 0.424242 |
| 2014-12-05 00:00:00+00:00 | 0.151515 | 0.31250 | 0.515152 | 0.53125 | 0.606061 |
[44]:
alphalens.plotting.plot_top_bottom_quantile_turnover(
quantile_turnover, turnover_period);
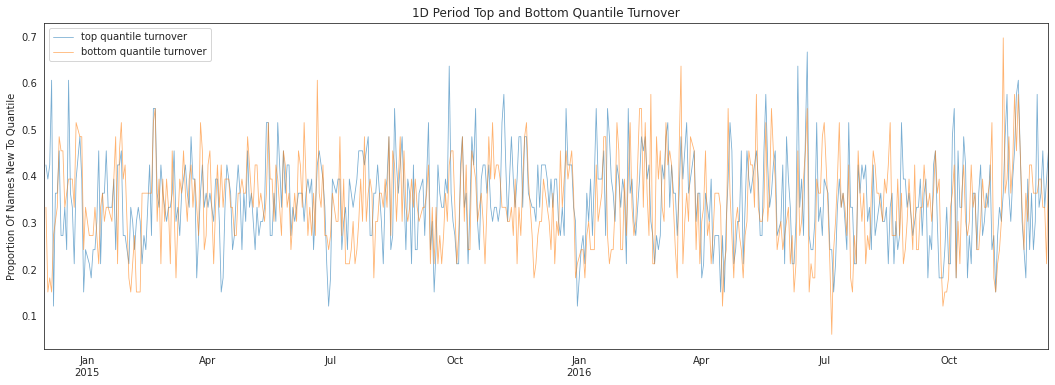
因子换手率非常重要,因为它反映了新信息的纳入以及信号极值部分的构成。通过观察顶部和底部分位数集合中的新增成分,我们可以了解该因子每天被重新构建的程度。
[45]:
factor_autocorrelation = alphalens.performance.factor_rank_autocorrelation(
factor_data, turnover_period)
[46]:
factor_autocorrelation.head()
[46]:
date
2014-12-01 00:00:00+00:00 NaN
2014-12-02 00:00:00+00:00 0.708640
2014-12-03 00:00:00+00:00 0.857790
2014-12-04 00:00:00+00:00 0.727252
2014-12-05 00:00:00+00:00 0.803030
Freq: C, Name: 1, dtype: float64
[47]:
alphalens.plotting.plot_factor_rank_auto_correlation(factor_autocorrelation);
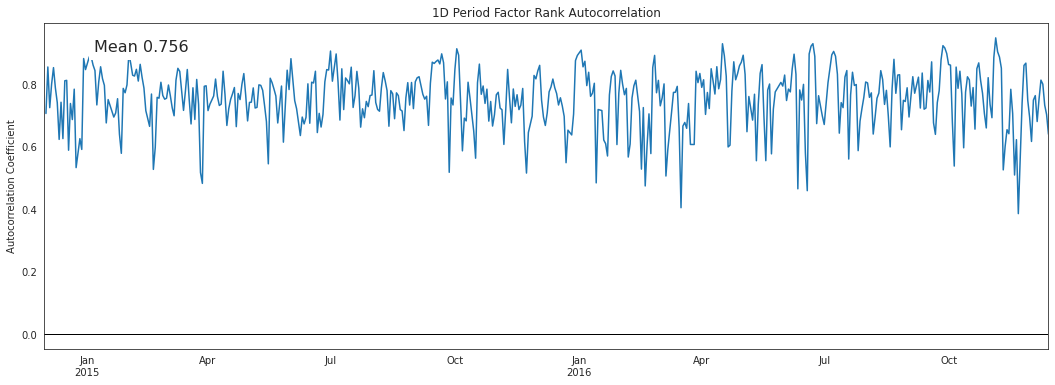
因子的自相关性向我们展示了信号本身的持续性。
换手率分析报告¶
我们可以一起查看所有换手率计算结果。
[49]:
alphalens.tears.create_turnover_tear_sheet(factor_data);
Turnover Analysis
| 1天 | 5天 | 10天 | |
|---|---|---|---|
| 第一分位数平均换手率 | 0.340 | 0.765 | 0.785 |
| 第二分位数平均换手率 | 0.601 | 0.791 | 0.799 |
| 三分位平均换手率 | 0.636 | 0.781 | 0.781 |
| 四分位4平均换手率 | 0.607 | 0.791 | 0.800 |
| 五分位平均换手率 | 0.350 | 0.783 | 0.793 |
| 1天 | 5天 | 10天 | |
|---|---|---|---|
| 因子排名平均自相关性 | 0.756 | 0.0 | -0.03 |
<Figure size 432x288 with 0 Axes>
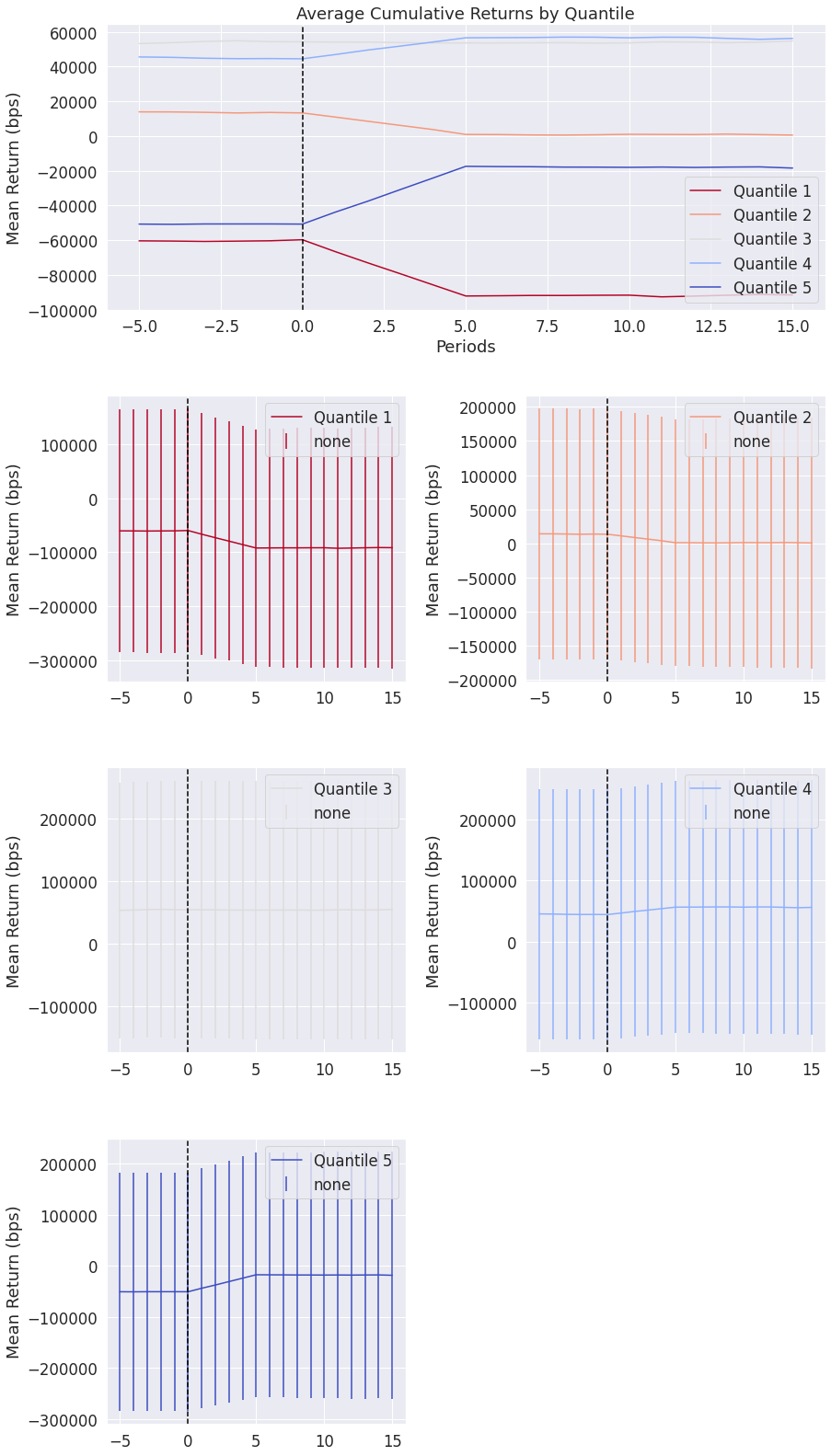
事件型收益率分析¶
观察因子前后窗口期的平均累积收益率,可以告诉我们该因子的预测效力能持续多久。这份分析报表需要较长时间才能运行完成。
注意: 本分析报表需要额外传入参数 pricing。
[50]:
alphalens.tears.create_event_returns_tear_sheet(
factor_data, pricing, by_group=True);
<Figure size 432x288 with 0 Axes>

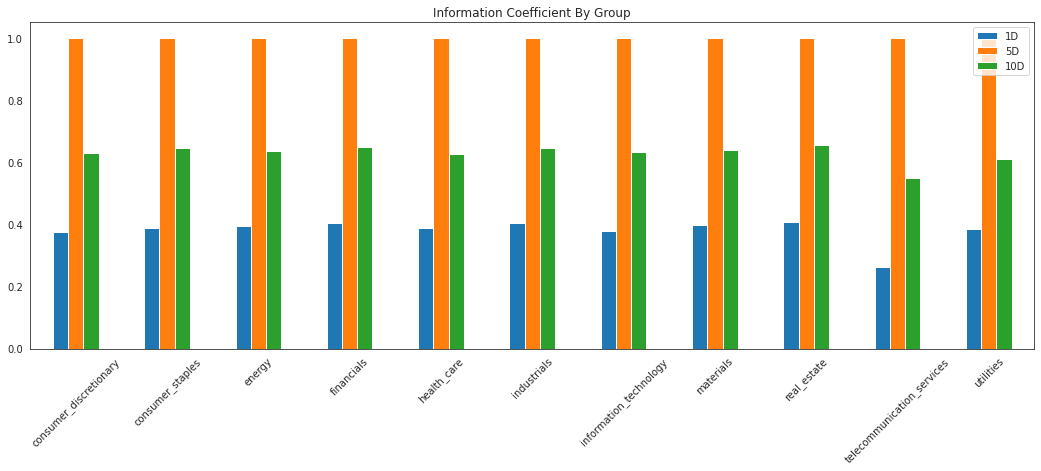
分组绩效分析¶
Alphalens中的许多图表如果提供了分组信息,可以按分组单独查看。通过传入by_group=True参数,可以按组查看收益和信息分析表。
[51]:
ic_by_sector = alphalens.performance.mean_information_coefficient(
factor_data, by_group=True)
[52]:
ic_by_sector.head()
[52]:
| 1天 | 5天 | 10天 | |
|---|---|---|---|
| 分组 | |||
| 非必需消费品 | 0.376525 | 1.0 | 0.630168 |
| 消费品 | 0.388736 | 1.0 | 0.645816 |
| 能量 | 0.394440 | 1.0 | 0.634939 |
| 金融数据 | 0.404388 | 1.0 | 0.648418 |
| 医疗保健 | 0.388439 | 1.0 | 0.627040 |
[53]:
alphalens.plotting.plot_ic_by_group(ic_by_sector)
[53]:
<AxesSubplot:title={'center':'Information Coefficient By Group'}>
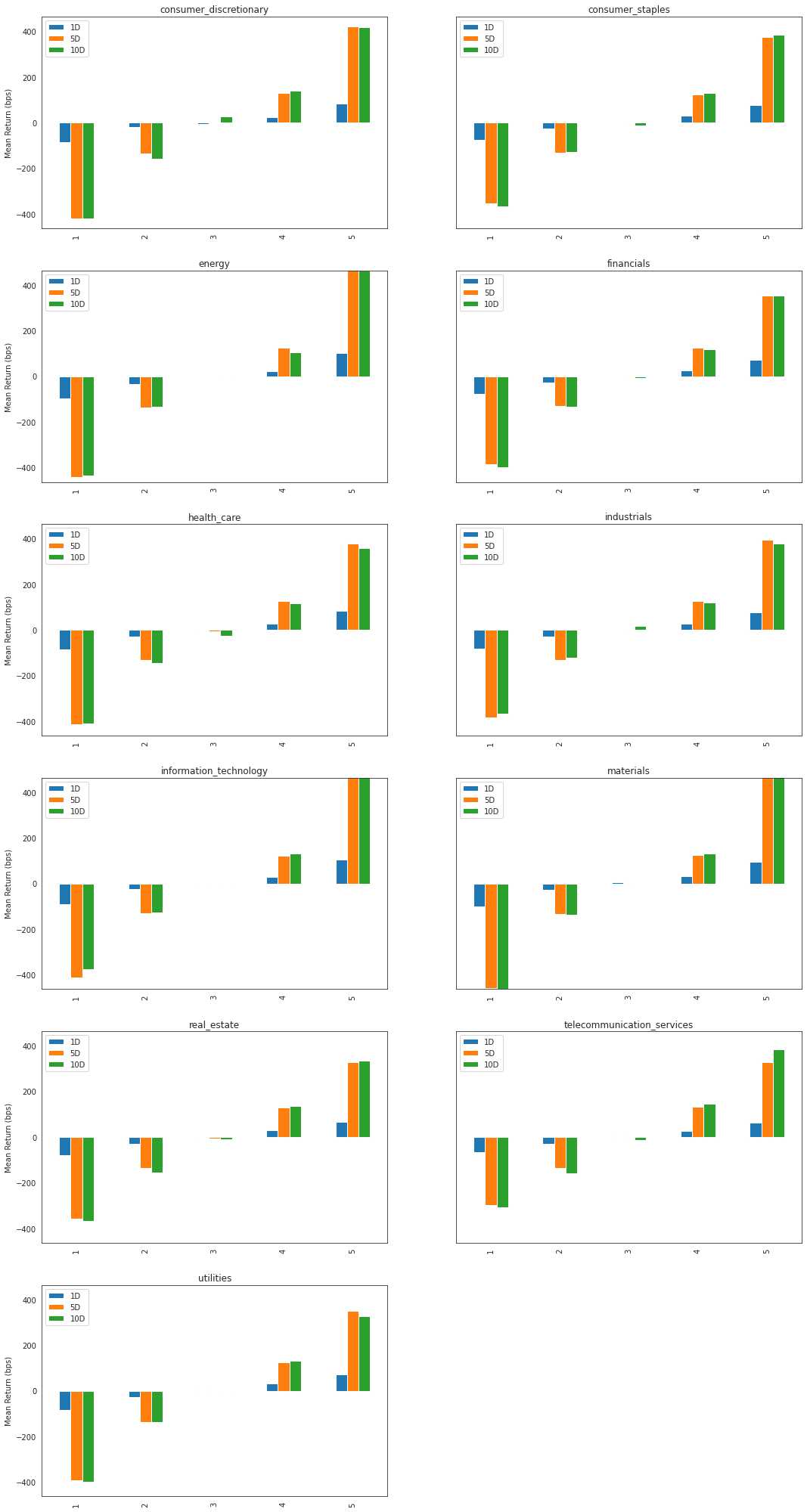
[54]:
mean_return_quantile_sector, mean_return_quantile_sector_err = alphalens.performance.mean_return_by_quantile(
factor_data, by_group=True)
[55]:
mean_return_quantile_sector.head()
[55]:
| 1天 | 5天 | 10天 | ||
|---|---|---|---|---|
| 因子分位数 | 分组 | |||
| 1 | 非必需消费品 | -0.008481 | -0.042084 | -0.041998 |
| 消费品行业 | -0.007378 | -0.035313 | -0.036838 | |
| 能量 | -0.009574 | -0.044188 | -0.043574 | |
| 金融板块 | -0.007825 | -0.038616 | -0.039761 | |
| 医疗保健 | -0.008552 | -0.041262 | -0.040898 |
[56]:
alphalens.plotting.plot_quantile_returns_bar(
mean_return_quantile_sector, by_group=True)
[56]:
array([<AxesSubplot:title={'center':'consumer_discretionary'}, ylabel='Mean Return (bps)'>,
<AxesSubplot:title={'center':'consumer_staples'}, ylabel='Mean Return (bps)'>,
<AxesSubplot:title={'center':'energy'}, ylabel='Mean Return (bps)'>,
<AxesSubplot:title={'center':'financials'}, ylabel='Mean Return (bps)'>,
<AxesSubplot:title={'center':'health_care'}, ylabel='Mean Return (bps)'>,
<AxesSubplot:title={'center':'industrials'}, ylabel='Mean Return (bps)'>,
<AxesSubplot:title={'center':'information_technology'}, ylabel='Mean Return (bps)'>,
<AxesSubplot:title={'center':'materials'}, ylabel='Mean Return (bps)'>,
<AxesSubplot:title={'center':'real_estate'}, ylabel='Mean Return (bps)'>,
<AxesSubplot:title={'center':'telecommunication_services'}, ylabel='Mean Return (bps)'>,
<AxesSubplot:title={'center':'utilities'}, ylabel='Mean Return (bps)'>,
<AxesSubplot:>], dtype=object)
汇总分析报告¶
上方有许多图表。如果您想快速了解alpha因子的表现情况,可以参考汇总分析报告。
[57]:
alphalens.tears.create_summary_tear_sheet(factor_data)
Quantiles Statistics
| 最小值 | 最大值 | 平均值 | 标准差 | 计数 | 计数百分比 | |
|---|---|---|---|---|---|---|
| 因子分位数 | ||||||
| 1 | -0.362876 | 0.034670 | -0.039407 | 0.032398 | 17028 | 20.245639 |
| 2 | -0.127588 | 0.046669 | -0.011804 | 0.019490 | 16513 | 19.633324 |
| 3 | -0.109737 | 0.068948 | 0.001341 | 0.018291 | 17026 | 20.243262 |
| 4 | -0.087449 | 0.098542 | 0.014397 | 0.019180 | 16512 | 19.632135 |
| 5 | -0.061661 | 0.494950 | 0.043818 | 0.036501 | 17028 | 20.245639 |
Returns Analysis
| 1天 | 5天 | 10天 | |
|---|---|---|---|
| 年化Alpha | 8.656 | 7.928 | 1.985 |
| beta | 0.094 | 0.080 | 0.062 |
| 最高分位组平均周期回报率 (基点) | 86.725 | 82.903 | 41.487 |
| 底部十分位数平均周期回报率(bps) | -86.236 | -83.545 | -41.947 |
| 周期平均价差(基点) | 172.960 | 166.458 | 83.458 |
Information Analysis
| 1天 | 5天 | 10天 | |
|---|---|---|---|
| IC均值 | 0.414 | 1.000000e+00 | 0.669 |
| IC标准差 | 0.175 | 0.000000e+00 | 0.127 |
| 风险调整后IC值 | 2.361 | 3.455090e+16 | 5.273 |
| t统计量(IC) | 53.633 | 7.848456e+17 | 119.777 |
| p值(IC) | 0.000 | 0.000000e+00 | 0.000 |
| IC偏度 | -0.673 | -3.840000e+00 | -1.034 |
| IC峰度 | 1.145 | 1.174300e+01 | 2.099 |
Turnover Analysis
| 1天 | 5天 | 10天 | |
|---|---|---|---|
| 第一分位数平均换手率 | 0.340 | 0.765 | 0.785 |
| 第二分位数平均换手率 | 0.601 | 0.791 | 0.799 |
| 三分位平均换手率 | 0.636 | 0.781 | 0.781 |
| 四分位4平均换手率 | 0.607 | 0.791 | 0.800 |
| 五分位平均换手率 | 0.350 | 0.783 | 0.793 |
| 1天 | 5天 | 10天 | |
|---|---|---|---|
| 因子排名平均自相关性 | 0.756 | 0.0 | -0.03 |
<Figure size 432x288 with 0 Axes>
整体概览¶
如需查看完整分析报告,请生成完整的数据分析表。通过传入因子数据,您可以一次性分析上述所有统计指标和图表。
[58]:
alphalens.tears.create_full_tear_sheet(factor_data)
Quantiles Statistics
| 最小值 | 最大值 | 平均值 | 标准差 | 计数 | 计数百分比 | |
|---|---|---|---|---|---|---|
| 因子分位数 | ||||||
| 1 | -0.362876 | 0.034670 | -0.039407 | 0.032398 | 17028 | 20.245639 |
| 2 | -0.127588 | 0.046669 | -0.011804 | 0.019490 | 16513 | 19.633324 |
| 3 | -0.109737 | 0.068948 | 0.001341 | 0.018291 | 17026 | 20.243262 |
| 4 | -0.087449 | 0.098542 | 0.014397 | 0.019180 | 16512 | 19.632135 |
| 5 | -0.061661 | 0.494950 | 0.043818 | 0.036501 | 17028 | 20.245639 |
Returns Analysis
| 1天 | 5天 | 10天 | |
|---|---|---|---|
| 年化Alpha | 8.656 | 7.928 | 1.985 |
| beta | 0.094 | 0.080 | 0.062 |
| 最高分位数的平均周期回报率 (基点) | 86.725 | 82.903 | 41.487 |
| 底部十分位平均周期收益率 (基点) | -86.236 | -83.545 | -41.947 |
| 周期平均价差(基点) | 172.960 | 166.458 | 83.458 |
<Figure size 432x288 with 0 Axes>
Information Analysis
| 1天 | 5天 | 10天 | |
|---|---|---|---|
| IC均值 | 0.414 | 1.000000e+00 | 0.669 |
| IC标准差 | 0.175 | 0.000000e+00 | 0.127 |
| 风险调整后IC值 | 2.361 | 3.455090e+16 | 5.273 |
| t统计量(IC) | 53.633 | 7.848456e+17 | 119.777 |
| p值(IC) | 0.000 | 0.000000e+00 | 0.000 |
| IC偏度 | -0.673 | -3.840000e+00 | -1.034 |
| IC峰度 | 1.145 | 1.174300e+01 | 2.099 |
Turnover Analysis
| 1天 | 5天 | 10天 | |
|---|---|---|---|
| 第一分位数平均换手率 | 0.340 | 0.765 | 0.785 |
| 第二分位数平均换手率 | 0.601 | 0.791 | 0.799 |
| 三分位平均换手率 | 0.636 | 0.781 | 0.781 |
| 四分位4平均换手率 | 0.607 | 0.791 | 0.800 |
| 五分位平均换手率 | 0.350 | 0.783 | 0.793 |
| 1天 | 5天 | 10天 | |
|---|---|---|---|
| 因子排名平均自相关性 | 0.756 | 0.0 | -0.03 |
