敏感性分析示例

方法

我们提供了五种敏感性分析方法，包括（安慰剂处理、随机原因、子集数据、随机替换和选择偏差）。本笔记本将逐步介绍如何使用组合函数 sensitivity_analysis() 来比较不同的方法，以及如何单独使用每种方法：

  1. 安慰剂处理：用随机变量替换处理

  2. 无关的额外混杂因素：添加一个随机共同原因变量

  3. 子集验证：移除数据的随机子集

  4. 选择偏差方法，包括单边混淆函数和对齐混淆函数

  5. 随机替换：随机将一个协变量替换为一个不相关的变量

[2]:

%matplotlib inline
%load_ext autoreload
%autoreload 2

[3]:

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
import warnings
import matplotlib
from causalml.inference.meta import BaseXLearner
from causalml.dataset import synthetic_data

from causalml.metrics.sensitivity import Sensitivity
from causalml.metrics.sensitivity import SensitivityRandomReplace, SensitivitySelectionBias

plt.style.use('fivethirtyeight')
matplotlib.rcParams['figure.figsize'] = [8, 8]
warnings.filterwarnings('ignore')

# logging.basicConfig(level=logging.INFO)

pd.options.display.float_format = '{:.4f}'.format

/Users/jing.pan/anaconda3/envs/causalml_3_6/lib/python3.6/site-packages/sklearn/utils/deprecation.py:144: FutureWarning: The sklearn.utils.testing module is  deprecated in version 0.22 and will be removed in version 0.24. The corresponding classes / functions should instead be imported from sklearn.utils. Anything that cannot be imported from sklearn.utils is now part of the private API.
  warnings.warn(message, FutureWarning)

生成合成数据

[4]:

# Generate synthetic data using mode 1
num_features = 6
y, X, treatment, tau, b, e = synthetic_data(mode=1, n=100000, p=num_features, sigma=1.0)

[5]:

tau.mean()

[5]:

0.5001096146567363

定义特征

[6]:

# Generate features names
INFERENCE_FEATURES = ['feature_' + str(i) for i in range(num_features)]
TREATMENT_COL = 'target'
OUTCOME_COL = 'outcome'
SCORE_COL = 'pihat'

[7]:

df = pd.DataFrame(X, columns=INFERENCE_FEATURES)
df[TREATMENT_COL] = treatment
df[OUTCOME_COL] = y
df[SCORE_COL] = e

[8]:

df.head()

[8]:
特征_0 特征_1 特征_2 特征_3 特征_4 特征_5 目标 结果 pihat
0 0.9536 0.2911 0.0432 0.8720 0.5190 0.0822 1 2.0220 0.7657
1 0.2390 0.3096 0.5115 0.2048 0.8914 0.5015 0 -0.0732 0.2304
2 0.1091 0.0765 0.7428 0.6951 0.4580 0.7800 0 -1.4947 0.1000
3 0.2055 0.3967 0.6278 0.2086 0.3865 0.8860 0 0.6458 0.2533
4 0.4501 0.0578 0.3972 0.4100 0.5760 0.4764 0 -0.0018 0.1000

包含所有协变量

敏感性分析总结报告（使用单侧混杂函数和默认alpha值）

[9]:

# Calling the Base XLearner class and return the sensitivity analysis summary report
learner_x = BaseXLearner(LinearRegression())
sens_x = Sensitivity(df=df, inference_features=INFERENCE_FEATURES, p_col='pihat',
                     treatment_col=TREATMENT_COL, outcome_col=OUTCOME_COL, learner=learner_x)
# Here for Selection Bias method will use default one-sided confounding function and alpha (quantile range of outcome values) input
sens_sumary_x = sens_x.sensitivity_analysis(methods=['Placebo Treatment',
                                                     'Random Cause',
                                                     'Subset Data',
                                                     'Random Replace',
                                                     'Selection Bias'], sample_size=0.5)

[10]:

# From the following results, refutation methods show our model is pretty robust;
# When alpah > 0, the treated group always has higher mean potential outcomes than the control; when  < 0, the control group is better off.
sens_sumary_x

[10]:
方法 ATE 新ATE 新ATE下限 新ATE上限
0 安慰剂治疗 0.6801 -0.0025 -0.0158 0.0107
0 随机原因 0.6801 0.6801 0.6673 0.6929
0 子集数据（样本大小 @0.5） 0.6801 0.6874 0.6693 0.7055
0 随机替换 0.6801 0.6799 0.6670 0.6929
0 选择偏差 (alpha@-0.80111, 具有 r-平方:... 0.6801 1.3473 1.3347 1.3599
0 选择偏差 (alpha@-0.64088, 与 r-平方:... 0.6801 1.2139 1.2013 1.2265
0 选择偏差 (alpha@-0.48066, 具有 r-平方:... 0.6801 1.0804 1.0678 1.0931
0 选择偏差 (alpha@-0.32044, 具有 r-平方:... 0.6801 0.9470 0.9343 0.9597
0 选择偏差 (alpha@-0.16022, 具有 r-平方:... 0.6801 0.8135 0.8008 0.8263
0 选择偏差 (alpha@0.0, 具有 r-平方:0.0 0.6801 0.6801 0.6673 0.6929
0 选择偏差 (alpha@0.16022, 与 r-平方:0... 0.6801 0.5467 0.5338 0.5595
0 选择偏差 (alpha@0.32044, 带有 r-平方:0... 0.6801 0.4132 0.4003 0.4261
0 选择偏差 (alpha@0.48066, 具有 r-平方:0... 0.6801 0.2798 0.2668 0.2928
0 选择偏差 (alpha@0.64088, 具有 r-平方:0... 0.6801 0.1463 0.1332 0.1594
0 选择偏差 (alpha@0.80111, 具有 r-平方:0... 0.6801 0.0129 -0.0003 0.0261

随机替换

[11]:

# Replace feature_0 with an irrelevent variable
sens_x_replace = SensitivityRandomReplace(df=df, inference_features=INFERENCE_FEATURES, p_col='pihat',
                                          treatment_col=TREATMENT_COL, outcome_col=OUTCOME_COL, learner=learner_x,
                                          sample_size=0.9, replaced_feature='feature_0')
s_check_replace = sens_x_replace.summary(method='Random Replace')
s_check_replace

[11]:
方法 ATE 新ATE 新ATE下限 新ATE上限
0 随机替换 0.6801 0.8072 0.7943 0.8200

选择偏差：对齐混淆函数

[12]:

sens_x_bias_alignment = SensitivitySelectionBias(df, INFERENCE_FEATURES, p_col='pihat', treatment_col=TREATMENT_COL,
                                                 outcome_col=OUTCOME_COL, learner=learner_x, confound='alignment',
                                                 alpha_range=None)

[13]:

lls_x_bias_alignment, partial_rsqs_x_bias_alignment = sens_x_bias_alignment.causalsens()

[14]:

lls_x_bias_alignment

[14]:
alpha rsqs 新ATE 新ATE下限 新ATE上限
0 -0.8011 0.1088 0.6685 0.6556 0.6813
0 -0.6409 0.0728 0.6708 0.6580 0.6836
0 -0.4807 0.0425 0.6731 0.6604 0.6859
0 -0.3204 0.0194 0.6754 0.6627 0.6882
0 -0.1602 0.0050 0.6778 0.6650 0.6905
0 0.0000 0.0000 0.6801 0.6673 0.6929
0 0.1602 0.0050 0.6824 0.6696 0.6953
0 0.3204 0.0200 0.6848 0.6718 0.6977
0 0.4807 0.0443 0.6871 0.6741 0.7001
0 0.6409 0.0769 0.6894 0.6763 0.7026
0 0.8011 0.1164 0.6918 0.6785 0.7050 
[15]:

partial_rsqs_x_bias_alignment

[15]:
特征 部分_rsqs
0 feature_0 -0.0631
1 feature_1 -0.0619
2 feature_2 -0.0001
3 feature_3 -0.0033
4 feature_4 -0.0001
5 feature_5 0.0000 
[16]:

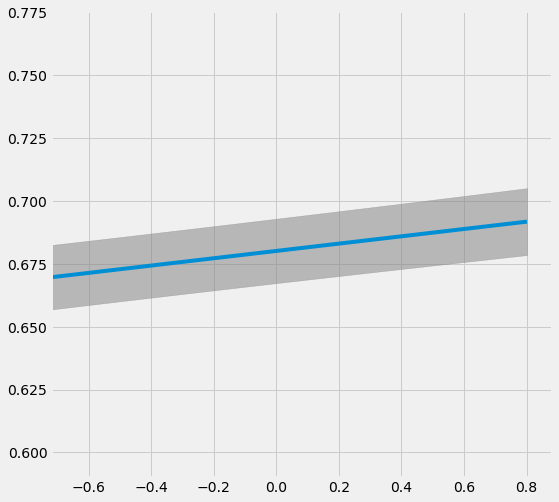
# Plot the results by confounding vector and plot Confidence Intervals for ATE
sens_x_bias_alignment.plot(lls_x_bias_alignment, ci=True)
../_images/examples_sensitivity_example_with_synthetic_data_22_0.png 
[17]:

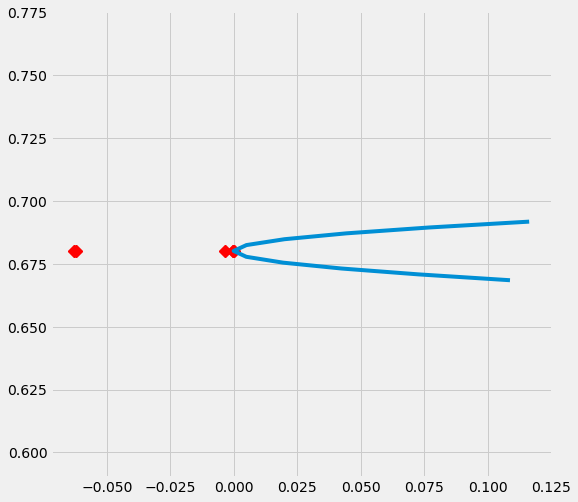
# Plot the results by rsquare with partial r-square results by each individual features
sens_x_bias_alignment.plot(lls_x_bias_alignment, partial_rsqs_x_bias_alignment, type='r.squared', partial_rsqs=True)
../_images/examples_sensitivity_example_with_synthetic_data_23_0.png

删除一个混淆变量

[18]:

df_new = df.drop('feature_0', axis=1).copy()
INFERENCE_FEATURES_new = INFERENCE_FEATURES.copy()
INFERENCE_FEATURES_new.remove('feature_0')
df_new.head()

[18]:
特征_1 特征_2 特征_3 特征_4 特征_5 目标 结果 pihat
0 0.2911 0.0432 0.8720 0.5190 0.0822 1 2.0220 0.7657
1 0.3096 0.5115 0.2048 0.8914 0.5015 0 -0.0732 0.2304
2 0.0765 0.7428 0.6951 0.4580 0.7800 0 -1.4947 0.1000
3 0.3967 0.6278 0.2086 0.3865 0.8860 0 0.6458 0.2533
4 0.0578 0.3972 0.4100 0.5760 0.4764 0 -0.0018 0.1000 
[19]:

INFERENCE_FEATURES_new

[19]:
['feature_1', 'feature_2', 'feature_3', 'feature_4', 'feature_5']

敏感性分析总结报告（使用单侧混杂函数和默认alpha值）

[20]:

sens_x_new = Sensitivity(df=df_new, inference_features=INFERENCE_FEATURES_new, p_col='pihat',
                     treatment_col=TREATMENT_COL, outcome_col=OUTCOME_COL, learner=learner_x)
# Here for Selection Bias method will use default one-sided confounding function and alpha (quantile range of outcome values) input
sens_sumary_x_new = sens_x_new.sensitivity_analysis(methods=['Placebo Treatment',
                                                     'Random Cause',
                                                     'Subset Data',
                                                     'Random Replace',
                                                     'Selection Bias'], sample_size=0.5)

[21]:

# Here we can see the New ATE restul from Random Replace method actually changed ~ 12.5%
sens_sumary_x_new

[21]:
方法 ATE 新ATE 新ATE下限 新ATE上限
0 安慰剂治疗 0.8072 0.0104 -0.0033 0.0242
0 随机原因 0.8072 0.8072 0.7943 0.8201
0 子集数据（样本大小 @0.5） 0.8072 0.8180 0.7998 0.8361
0 随机替换 0.8072 0.8068 0.7938 0.8198
0 选择偏差 (alpha@-0.80111, 与 r-平方:... 0.8072 1.3799 1.3673 1.3925
0 选择偏差 (alpha@-0.64088, 与 r-平方:... 0.8072 1.2654 1.2527 1.2780
0 选择偏差 (alpha@-0.48066, 具有 r-平方:... 0.8072 1.1508 1.1381 1.1635
0 选择偏差 (alpha@-0.32044, 具有 r-平方:... 0.8072 1.0363 1.0235 1.0490
0 选择偏差 (alpha@-0.16022, 与 r-平方:... 0.8072 0.9217 0.9089 0.9345
0 选择偏差 (alpha@0.0, 带有 r-平方:0.0 0.8072 0.8072 0.7943 0.8200
0 选择偏差 (alpha@0.16022, 与 r-平方:0... 0.8072 0.6926 0.6796 0.7056
0 选择偏差 (alpha@0.32044, 具有 r-平方:0... 0.8072 0.5780 0.5650 0.5911
0 选择偏差 (alpha@0.48066, 具有 r-平方:0... 0.8072 0.4635 0.4503 0.4767
0 选择偏差 (alpha@0.64088, 与 r-平方:0... 0.8072 0.3489 0.3356 0.3623
0 选择偏差 (alpha@0.80111, 具有 r-平方:0... 0.8072 0.2344 0.2209 0.2479

随机替换

[22]:

# Replace feature_0 with an irrelevent variable
sens_x_replace_new = SensitivityRandomReplace(df=df_new, inference_features=INFERENCE_FEATURES_new, p_col='pihat',
                                          treatment_col=TREATMENT_COL, outcome_col=OUTCOME_COL, learner=learner_x,
                                          sample_size=0.9, replaced_feature='feature_1')
s_check_replace_new = sens_x_replace_new.summary(method='Random Replace')
s_check_replace_new

[22]:
方法 ATE 新ATE 新ATE下限 新ATE上限
0 随机替换 0.8072 0.9022 0.8893 0.9152

选择偏差：对齐混淆函数

[23]:

sens_x_bias_alignment_new = SensitivitySelectionBias(df_new, INFERENCE_FEATURES_new, p_col='pihat', treatment_col=TREATMENT_COL,
                                                 outcome_col=OUTCOME_COL, learner=learner_x, confound='alignment',
                                                 alpha_range=None)

[24]:

lls_x_bias_alignment_new, partial_rsqs_x_bias_alignment_new = sens_x_bias_alignment_new.causalsens()

[25]:

lls_x_bias_alignment_new

[25]:
alpha rsqs 新ATE 新ATE下限 新ATE上限
0 -0.8011 0.1121 0.7919 0.7789 0.8049
0 -0.6409 0.0732 0.7950 0.7820 0.8079
0 -0.4807 0.0419 0.7980 0.7851 0.8109
0 -0.3204 0.0188 0.8011 0.7882 0.8139
0 -0.1602 0.0047 0.8041 0.7912 0.8170
0 0.0000 0.0000 0.8072 0.7943 0.8200
0 0.1602 0.0048 0.8102 0.7973 0.8231
0 0.3204 0.0189 0.8133 0.8003 0.8262
0 0.4807 0.0420 0.8163 0.8032 0.8294
0 0.6409 0.0736 0.8194 0.8062 0.8325
0 0.8011 0.1127 0.8224 0.8091 0.8357 
[26]:

partial_rsqs_x_bias_alignment_new

[26]:
特征 部分_rsqs
0 feature_1 -0.0345
1 feature_2 -0.0001
2 feature_3 -0.0038
3 feature_4 -0.0001
4 feature_5 0.0000 
[27]:

# Plot the results by confounding vector and plot Confidence Intervals for ATE
sens_x_bias_alignment_new.plot(lls_x_bias_alignment_new, ci=True)
../_images/examples_sensitivity_example_with_synthetic_data_37_0.png 
[28]:

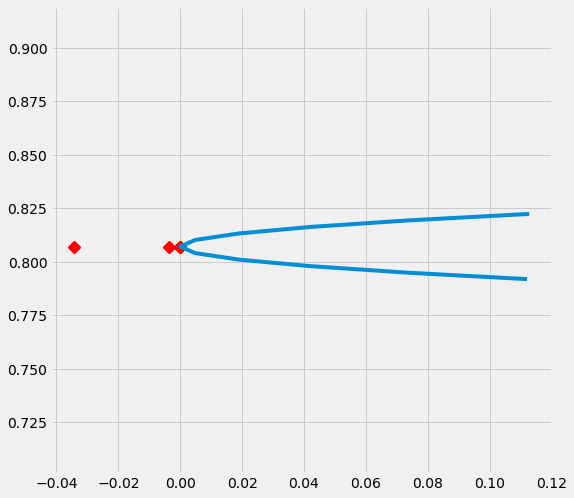
# Plot the results by rsquare with partial r-square results by each individual features
sens_x_bias_alignment_new.plot(lls_x_bias_alignment_new, partial_rsqs_x_bias_alignment_new, type='r.squared', partial_rsqs=True)
../_images/examples_sensitivity_example_with_synthetic_data_38_0.png

生成一个选择偏差集

[29]:

df_new_2 = df.copy()
df_new_2['treated_new'] = df['feature_0'].rank()
df_new_2['treated_new'] = [1 if i > df_new_2.shape[0]/2 else 0 for i in df_new_2['treated_new']]

[30]:

df_new_2.head()

[30]:
特征_0 特征_1 特征_2 特征_3 特征_4 特征_5 目标 结果 pihat treated_new
0 0.9536 0.2911 0.0432 0.8720 0.5190 0.0822 1 2.0220 0.7657 1
1 0.2390 0.3096 0.5115 0.2048 0.8914 0.5015 0 -0.0732 0.2304 0
2 0.1091 0.0765 0.7428 0.6951 0.4580 0.7800 0 -1.4947 0.1000 0
3 0.2055 0.3967 0.6278 0.2086 0.3865 0.8860 0 0.6458 0.2533 0
4 0.4501 0.0578 0.3972 0.4100 0.5760 0.4764 0 -0.0018 0.1000 0

敏感性分析总结报告（使用单侧混杂函数和默认alpha值）

[31]:

sens_x_new_2 = Sensitivity(df=df_new_2, inference_features=INFERENCE_FEATURES, p_col='pihat',
                     treatment_col='treated_new', outcome_col=OUTCOME_COL, learner=learner_x)
# Here for Selection Bias method will use default one-sided confounding function and alpha (quantile range of outcome values) input
sens_sumary_x_new_2 = sens_x_new_2.sensitivity_analysis(methods=['Placebo Treatment',
                                                     'Random Cause',
                                                     'Subset Data',
                                                     'Random Replace',
                                                     'Selection Bias'], sample_size=0.5)

[32]:

sens_sumary_x_new_2

[32]:
方法 ATE 新ATE 新ATE下限 新ATE上限
0 安慰剂治疗 0.0432 0.0081 -0.0052 0.0213
0 随机原因 0.0432 0.0432 0.0296 0.0568
0 子集数据（样本大小 @0.5） 0.0432 0.0976 0.0784 0.1167
0 随机替换 0.0432 0.0433 0.0297 0.0568
0 选择偏差 (alpha@-0.80111, 具有 r-平方:... 0.0432 0.8369 0.8239 0.8499
0 选择偏差 (alpha@-0.64088, 与 r-平方:... 0.0432 0.6782 0.6651 0.6913
0 选择偏差 (alpha@-0.48066, 具有 r-平方:... 0.0432 0.5194 0.5063 0.5326
0 选择偏差 (alpha@-0.32044, 具有 r-平方:... 0.0432 0.3607 0.3474 0.3740
0 选择偏差 (alpha@-0.16022, 具有 r-平方:... 0.0432 0.2020 0.1885 0.2154
0 选择偏差 (alpha@0.0, 带有 r-平方:0.0 0.0432 0.0432 0.0296 0.0568
0 选择偏差 (alpha@0.16022, 具有 r-平方:0... 0.0432 -0.1155 -0.1293 -0.1018
0 选择偏差 (alpha@0.32044, 具有 r-平方:0... 0.0432 -0.2743 -0.2882 -0.2604
0 选择偏差 (alpha@0.48066, 具有 r-平方:0... 0.0432 -0.4330 -0.4471 -0.4189
0 选择偏差 (alpha@0.64088, 具有 r-平方:0... 0.0432 -0.5918 -0.6060 -0.5775
0 选择偏差 (alpha@0.80111, 具有 r-平方:0... 0.0432 -0.7505 -0.7650 -0.7360

随机替换

[33]:

# Replace feature_0 with an irrelevent variable
sens_x_replace_new_2 = SensitivityRandomReplace(df=df_new_2, inference_features=INFERENCE_FEATURES, p_col='pihat',
                                          treatment_col='treated_new', outcome_col=OUTCOME_COL, learner=learner_x,
                                          sample_size=0.9, replaced_feature='feature_0')
s_check_replace_new_2 = sens_x_replace_new_2.summary(method='Random Replace')
s_check_replace_new_2

[33]:
方法 ATE 新ATE 新ATE下限 新ATE上限
0 随机替换 0.0432 0.4847 0.4713 0.4981

选择偏差：对齐混淆函数

[34]:

sens_x_bias_alignment_new_2 = SensitivitySelectionBias(df_new_2, INFERENCE_FEATURES, p_col='pihat', treatment_col='treated_new',
                                                 outcome_col=OUTCOME_COL, learner=learner_x, confound='alignment',
                                                 alpha_range=None)

[35]:

lls_x_bias_alignment_new_2, partial_rsqs_x_bias_alignment_new_2 = sens_x_bias_alignment_new_2.causalsens()

[36]:

lls_x_bias_alignment_new_2

[36]:
alpha rsqs 新ATE 新ATE下限 新ATE上限
0 -0.8011 0.0604 -0.2260 -0.2399 -0.2120
0 -0.6409 0.0415 -0.1721 -0.1860 -0.1583
0 -0.4807 0.0250 -0.1183 -0.1320 -0.1045
0 -0.3204 0.0119 -0.0645 -0.0781 -0.0508
0 -0.1602 0.0032 -0.0106 -0.0242 0.0030
0 0.0000 0.0000 0.0432 0.0296 0.0568
0 0.1602 0.0035 0.0971 0.0835 0.1106
0 0.3204 0.0148 0.1509 0.1373 0.1645
0 0.4807 0.0347 0.2047 0.1911 0.2183
0 0.6409 0.0635 0.2586 0.2449 0.2722
0 0.8011 0.1013 0.3124 0.2986 0.3262 
[37]:

partial_rsqs_x_bias_alignment_new_2

[37]:
特征 部分_rsqs
0 feature_0 -0.4041
1 feature_1 0.0101
2 feature_2 0.0000
3 feature_3 0.0016
4 feature_4 0.0011
5 feature_5 0.0000 
[38]:

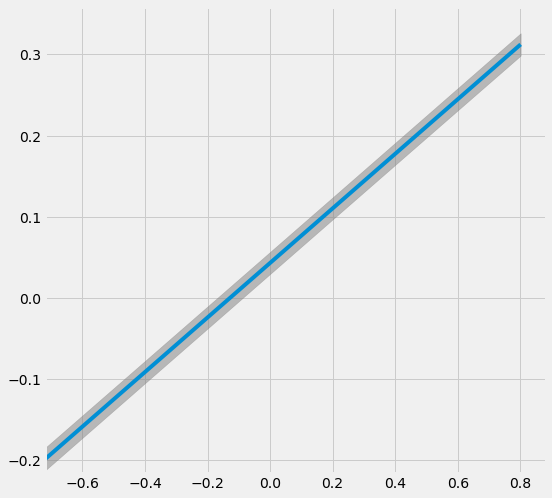
# Plot the results by confounding vector and plot Confidence Intervals for ATE
sens_x_bias_alignment_new_2.plot(lls_x_bias_alignment_new_2, ci=True)
../_images/examples_sensitivity_example_with_synthetic_data_52_0.png 
[39]:

# Plot the results by rsquare with partial r-square results by each individual features
sens_x_bias_alignment_new_2.plot(lls_x_bias_alignment_new, partial_rsqs_x_bias_alignment_new_2, type='r.squared', partial_rsqs=True)
../_images/examples_sensitivity_example_with_synthetic_data_53_0.png