零和游戏¶
问题定义和研究动机¶
零和游戏,是博弈论中的一个经典概念,意味着游戏中所有参与者的利益总和为零。根据参与者的数量,零和游戏可以分为两人零和游戏和多人零和游戏。
经典的双人零和游戏场景,如石头剪刀布,其中一方获胜,另一方失败,意味着当一方获得收益时,不可避免地会给另一方带来等量的损失。
在两人零和博弈的研究中,普遍认为困难在于找到这个问题的解决方案,即纳什均衡解。
研究历史¶
随着学者们对零和博弈方向的研究不断深入,主要有以下几个发展阶段:
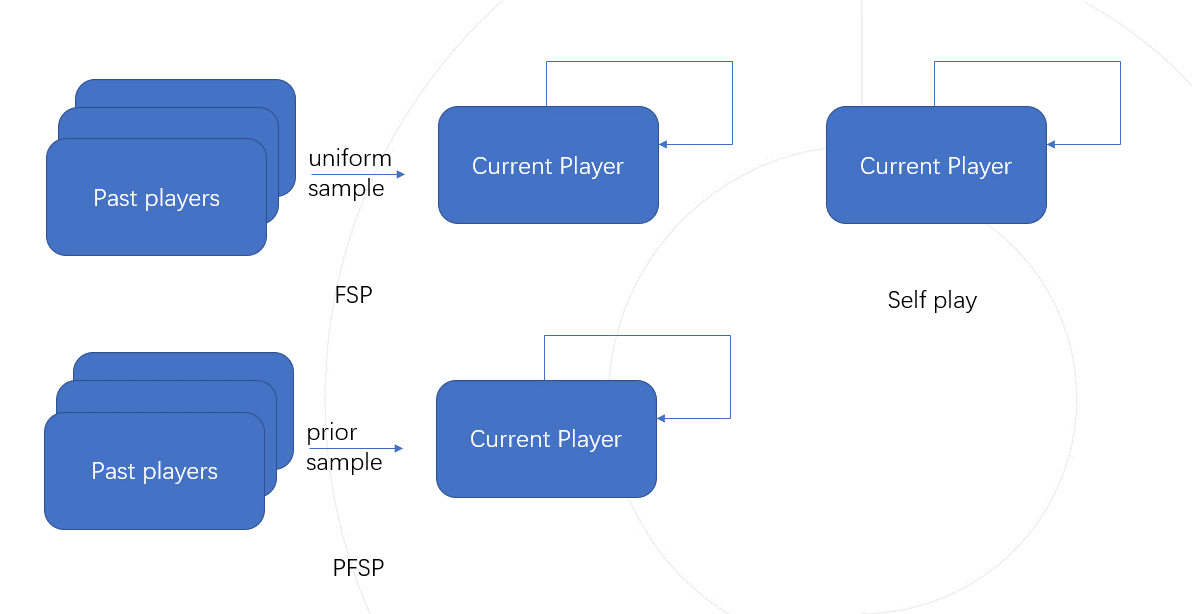
1. 自我对弈, SP
自我对弈指的是与自己进行训练,通常用于解决棋盘游戏并为一般游戏建立基准。AlphaZero和OpenAI Five通过仅进行自我对弈而不使用任何人类数据,已经达到了超越人类的水平。 尽管自我对弈在许多游戏类型中可以实现超越人类水平的表现,但它也有缺点。例如,假设在石头剪刀布游戏中的人类策略是只出剪刀,那么自我对弈模型将在一个类似于石头剪刀布的序列中无限循环。
2. 虚拟自我对弈, FSP [[1]]
为了解决自我对弈的限制问题,FSP引入了训练智能体的过去版本进行训练,并在自我对弈的基础上,过去版本的智能体也会以相同的概率随机相互对抗,这种训练方法被称为虚拟自我对弈。由于对手池的多样性,无论我们的初始策略如何,FSP都会收敛到一个均匀随机的石头剪刀布混合策略,这也是该问题的纳什均衡解。
3. 优先虚构自我对弈,PFSP [[2]]
PFSP(优先虚拟自对弈)基于FSP,它根据训练智能体与历史智能体之间的匹配率分配对手,并增加训练智能体与匹配率较低的历史智能体对战的频率,以实现更快的收敛,这种训练方法被称为优先虚拟自对弈。星际争霸2的AI AlphaStar [[3]] 使用PFSP来辅助训练。
未来展望¶
如何设计更高效的匹配策略,以使用更少的训练资源获得更强的智能。
相应的设计在许多工程项目中都有应用(ALphaStar, TstarBot [[4]]),但通常是经验性的(依赖于主观的人类判断),并且很少从理论上论证为什么它们是高效的。
如何考虑多人零和游戏以及更一般的多人游戏。
