Table of Contents
Shortcuts

DDPG

概述

DDPG (Deep Deterministic Policy Gradient) 首次在论文 Continuous control with deep reinforcement learning 中提出, 是一种同时学习Q函数和策略函数的算法。

DDPG 是基于 DPG (deterministic policy gradient) 的 无模型（model-free） 算法，属于 演员—评委（actor-critic） 方法中的一员，可以在高维、连续的动作空间上运行。 其中算法 DPG Deterministic policy gradient algorithms 与算法 NFQCA Reinforcement learning in feedback control 相似。

核心要点

  1. DDPG 仅支持 连续动作空间 （例如： MuJoCo）.

  2. DDPG 是一种 异策略（off-policy） 算法.

  3. DDPG 是一种 无模型（model-free） 和 演员—评委（actor-critic） 的强化学习算法，它会分别优化策略网络和Q网络。

  4. 通常, DDPG 使用 奥恩斯坦-乌伦贝克过程（Ornstein-Uhlenbeck process） 或 高斯过程（Gaussian process） （在我们的实现中默认使用高斯过程）来探索环境。

关键方程或关键框图

DDPG 包含一个参数化的策略函数（actor） \(\mu\left(s \mid \theta^{\mu}\right)\) , 此函数通过将每一个状态确定性地映射到一个具体的动作从而明确当前策略。 此外，算法还包含一个参数化的Q函数（critic） \(Q(s, a)\) 。 正如 Q-learning 算法，此函数通过贝尔曼方程优化自身。

策略网络通过将链式法则应用于初始分布的预期收益 \(J\) 来更新自身参数。

具体而言，为了最大化预期收益 \(J\) ，算法需要计算 \(J\) 对策略函数参数 \(\theta^{\mu}\) 的梯度。 \(J\) 是 \(Q(s, a)\) 的期望，所以问题转化为计算 \(Q^{\mu}(s, \mu(s))\) 对 \(\theta^{\mu}\) 的梯度。

根据链式法则，\(\nabla_{\theta^{\mu}} Q^{\mu}(s, \mu(s)) = \nabla_{\theta^{\mu}}\mu(s)\nabla_{a}Q^\mu(s,a)|_{ a=\mu\left(s\right)}+\nabla_{\theta^{\mu}} Q^{\mu}(s, a)|_{ a=\mu\left(s\right)}\)。

Deterministic policy gradient algorithms 采取了与 Off-Policy Actor-Critic 中推导 异策略版本的随机性策略梯度定理 类似的做法，舍去了上式第二项， 从而得到了近似后的 确定性策略梯度定理 ：

\[\begin{split}\begin{aligned} \nabla_{\theta^{\mu}} J & \approx \mathbb{E}_{s_{t} \sim \rho^{\beta}}\left[\left.\nabla_{\theta^{\mu}} Q\left(s, a \mid \theta^{Q}\right)\right|_{s=s_{t}, a=\mu\left(s_{t} \mid \theta^{\mu}\right)}\right] \\ &=\mathbb{E}_{s_{t} \sim \rho^{\beta}}\left[\left.\left.\nabla_{a} Q\left(s, a \mid \theta^{Q}\right)\right|_{s=s_{t}, a=\mu\left(s_{t}\right)} \nabla_{\theta^{\mu}} \mu\left(s \mid \theta^{\mu}\right)\right|_{s=s_{t}}\right] \end{aligned}\end{split}\]

DDPG 使用了一个 经验回放池（replay buffer） 来保证样本分布独立一致。

为了使神经网络稳定优化，DDPG 使用 软更新（“soft” target updates） 的方式来优化目标网络，而不是像 DQN 中的 hard target updates 那样定期直接复制网络的参数。 具体而言，DDPG 分别拷贝了 actor 网络 \(\mu' \left(s \mid \theta^{\mu'}\right)\) 和 critic 网络 \(Q'(s, a|\theta^{Q'})\) 用于计算目标值。 然后通过让这些目标网络缓慢跟踪学习到的网络来更新这些目标网络的权重：

\[\theta' \leftarrow \tau \theta + (1 - \tau)\theta',\]

其中 \(\tau<<1\)。这意味着目标值被限制为缓慢变化，大大提高了学习的稳定性。

在连续行动空间中学习的一个主要挑战是探索。然而，对于像DDPG这样的 异策略（off-policy） 算法来说，它的一个优势是可以独立于算法中的学习过程来处理探索问题。具体来说，我们通过将噪声过程 \(\mathcal{N}\) 采样的噪声添加到 actor 策略中来构建探索策略:

\[\mu^{\prime}\left(s_{t}\right)=\mu\left(s_{t} \mid \theta_{t}^{\mu}\right)+\mathcal{N}\]

伪代码

\[ \begin{align}\begin{aligned}:nowrap:\\\begin{split}\begin{algorithm}[H] \caption{Deep Deterministic Policy Gradient} \label{alg1} \begin{algorithmic}[1] \STATE Input: initial policy parameters $\theta$, Q-function parameters $\phi$, empty replay buffer $\mathcal{D}$ \STATE Set target parameters equal to main parameters $\theta_{\text{targ}} \leftarrow \theta$, $\phi_{\text{targ}} \leftarrow \phi$ \REPEAT \STATE Observe state $s$ and select action $a = \text{clip}(\mu_{\theta}(s) + \epsilon, a_{Low}, a_{High})$, where $\epsilon \sim \mathcal{N}$ \STATE Execute $a$ in the environment \STATE Observe next state $s'$, reward $r$, and done signal $d$ to indicate whether $s'$ is terminal \STATE Store $(s,a,r,s',d)$ in replay buffer $\mathcal{D}$ \STATE If $s'$ is terminal, reset environment state. \IF{it's time to update} \FOR{however many updates} \STATE Randomly sample a batch of transitions, $B = \{ (s,a,r,s',d) \}$ from $\mathcal{D}$ \STATE Compute targets \begin{equation*} y(r,s',d) = r + \gamma (1-d) Q_{\phi_{\text{targ}}}(s', \mu_{\theta_{\text{targ}}}(s')) \end{equation*} \STATE Update Q-function by one step of gradient descent using \begin{equation*} \nabla_{\phi} \frac{1}{|B|}\sum_{(s,a,r,s',d) \in B} \left( Q_{\phi}(s,a) - y(r,s',d) \right)^2 \end{equation*} \STATE Update policy by one step of gradient ascent using \begin{equation*} \nabla_{\theta} \frac{1}{|B|}\sum_{s \in B}Q_{\phi}(s, \mu_{\theta}(s)) \end{equation*} \STATE Update target networks with \begin{align*} \phi_{\text{targ}} &\leftarrow \rho \phi_{\text{targ}} + (1-\rho) \phi \\ \theta_{\text{targ}} &\leftarrow \rho \theta_{\text{targ}} + (1-\rho) \theta \end{align*} \ENDFOR \ENDIF \UNTIL{convergence} \end{algorithmic} \end{algorithm}\end{split}\end{aligned}\end{align} \]
../_images/DDPG.jpg

扩展

DDPG 可以与以下技术相结合使用:

  • 目标网络

    Continuous control with deep reinforcement learning 提出了利用软目标更新保持网络训练稳定的方法。 因此我们通过 model_wrap 中的 TargetNetworkWrapper 和配置 learn.target_theta 来实现 演员—评委（actor-critic） 的软更新目标网络。

  • 遵循随机策略的经验回放池初始采集

    在优化模型参数前，我们需要让经验回放池存有足够数目的遵循随机策略的 transition 数据，从而确保在算法初期模型不会对经验回放池数据过拟合。 因此我们通过配置 random-collect-size 来控制初始经验回放池中的 transition 数目。 DDPG/TD3 的 random-collect-size 默认设置为25000, SAC 为10000。 我们只是简单地遵循 SpinningUp 默认设置，并使用随机策略来收集初始化数据。

  • 采集过渡过程中的高斯噪声

    对于探索噪声过程，DDPG使用时间相关噪声，以提高具有惯性的物理控制问题的探索效率。 具体而言，DDPG 使用 Ornstein-Uhlenbeck 过程，其中 \(\theta = 0.15\) 且 \(\sigma = 0.2\)。Ornstein-Uhlenbeck 过程模拟了带有摩擦的布朗粒子的速度，其结果是以 0 为中心的时间相关值。 然而，由于 Ornstein-Uhlenbeck 噪声的超参数太多，我们使用高斯噪声代替了 Ornstein-Uhlenbeck 噪声。 我们通过配置 collect.noise_sigma 来控制探索程度。

实现

默认配置定义如下:

class ding.policy.ddpg.DDPGPolicy(cfg: EasyDict, model: Module | None = None, enable_field: List[str] | None = None)[source]
Overview:

DDPG算法的策略类。论文链接：https://arxiv.org/abs/1509.02971.

Config:

ID

符号

类型

默认值

描述

其他（形状）

1
type

字符串

ddpg
RL policy register name, refer
to registry POLICY_REGISTRY
this arg is optional,
a placeholder

2
cuda

布尔

假
Whether to use cuda for network

3
random_
collect_size

整数

25000
Number of randomly collected
training samples in replay
buffer when training starts.
Default to 25000 for
DDPG/TD3, 10000 for
sac.

4
model.twin_
critic

布尔

假
Whether to use two critic
networks or only one.
Default False for
DDPG, Clipped Double
Q-learning method in
TD3 paper.

5
learn.learning
_rate_actor

浮点数

1e-3
Learning rate for actor
network(aka. policy).


6
learn.learning
_rate_critic

浮点数

1e-3
Learning rates for critic
network (aka. Q-network).


7
learn.actor_
update_freq

整数

2
When critic network updates
once, how many times will actor
network update.
Default 1 for DDPG,
2 for TD3. Delayed
Policy Updates method
in TD3 paper.

8
learn.noise

布尔

假
Whether to add noise on target
network’s action.
Default False for
DDPG, True for TD3.
Target Policy Smoo-
thing Regularization
in TD3 paper.

9
learn.-
ignore_done

布尔

假
Determine whether to ignore
done flag.
Use ignore_done only
in halfcheetah env.

10
learn.-
target_theta

浮点数

0.005
Used for soft update of the
target network.
aka. Interpolation
factor in polyak aver-
aging for target
networks.

11
collect.-
noise_sigma

浮点数

0.1
Used for add noise during co-
llection, through controlling
the sigma of distribution
Sample noise from dis-
tribution, Ornstein-
Uhlenbeck process in
DDPG paper, Gaussian
process in ours.

模型

在这里，我们提供了 ContinuousQAC 模型作为 DDPG 的默认模型的示例。

class ding.model.ContinuousQAC(obs_shape: int | SequenceType, action_shape: int | SequenceType | EasyDict, action_space: str, twin_critic: bool = False, actor_head_hidden_size: int = 64, actor_head_layer_num: int = 1, critic_head_hidden_size: int = 64, critic_head_layer_num: int = 1, activation: Module | None = ReLU(), norm_type: str | None = None, encoder_hidden_size_list: SequenceType | None = None, share_encoder: bool | None = False)[source]
Overview:

与Q值演员-评论家（QAC）相关的算法的神经网络和计算图，例如DDPG/TD3/SAC。该模型现在支持连续和混合动作空间。ContinuousQAC由四部分组成：actor_encoder、critic_encoder、actor_head和critic_head。编码器用于从各种观察中提取特征。头部用于预测相应的Q值或动作逻辑。在高维观察空间（如2D图像）中，我们通常为actor_encoder和critic_encoder使用共享编码器。在低维观察空间（如1D向量）中，我们通常使用不同的编码器。

Interfaces:

__init__, forward, compute_actor, compute_critic

compute_actor(obs: Tensor) → Dict[str, Tensor | Dict[str, Tensor]][source]
Overview:

QAC 前向计算图用于演员部分，输入观察张量以预测动作或动作对数。

Arguments:

  • x (torch.Tensor): 输入的观测张量数据。

Returns:

  • 输出 (Dict[str, Union[torch.Tensor, Dict[str, torch.Tensor]]]): 根据动作空间变化的Actor输出字典：regression, reparameterization, hybrid。

ReturnsKeys (regression):

  • 动作 (torch.Tensor): 与 action_shape 大小相同的连续动作，通常在 DDPG/TD3 中使用。

ReturnsKeys (reparameterization):

  • logit (Dict[str, torch.Tensor]): 预测的重新参数化动作logit，通常在SAC中使用。它是一个包含两个张量的列表：mu 和 sigma。前者是高斯分布的均值，后者是高斯分布的标准差。

ReturnsKeys (hybrid):

  • logit (torch.Tensor): 预测的离散动作类型的logit，它将与action_type_shape具有相同的维度，即所有可能的离散动作类型。

  • action_args (torch.Tensor): 连续动作参数，大小与 action_args_shape 相同。

Shapes:

  • obs (torch.Tensor): \((B, N0)\), B 是批量大小，N0 对应于 obs_shape。

  • 动作 (torch.Tensor): \((B, N1)\), B 是批量大小，N1 对应于 action_shape。

  • logit.mu (torch.Tensor): \((B, N1)\), B 是批量大小，N1 对应于 action_shape。

  • logit.sigma (torch.Tensor): \((B, N1)\), B 是批量大小。

  • logit (torch.Tensor): \((B, N2)\), B 是批量大小，N2 对应于 action_shape.action_type_shape。

  • action_args (torch.Tensor): \((B, N3)\), B 是批量大小，N3 对应于 action_shape.action_args_shape。

Examples:
>>> # Regression mode
>>> model = ContinuousQAC(64, 6, 'regression')
>>> obs = torch.randn(4, 64)
>>> actor_outputs = model(obs,'compute_actor')
>>> assert actor_outputs['action'].shape == torch.Size([4, 6])
>>> # Reparameterization Mode
>>> model = ContinuousQAC(64, 6, 'reparameterization')
>>> obs = torch.randn(4, 64)
>>> actor_outputs = model(obs,'compute_actor')
>>> assert actor_outputs['logit'][0].shape == torch.Size([4, 6])  # mu
>>> actor_outputs['logit'][1].shape == torch.Size([4, 6]) # sigma
compute_critic(inputs: Dict[str, Tensor]) → Dict[str, Tensor][source]
Overview:

QAC 前向计算图用于评论家部分，输入观察和动作张量以预测 Q 值。

Arguments:

  • 输入 (Dict[str, torch.Tensor]): 输入数据的字典，包括 obs 和 action 张量，在混合动作空间中还包含 logit 和 action_args 张量。

ArgumentsKeys:

  • obs: (torch.Tensor): 观测张量数据，现在支持一批一维向量数据。

  • 动作 (Union[torch.Tensor, Dict]): 与 action_shape 大小相同的连续动作。

  • logit (torch.Tensor): 离散动作的logit，仅在混合动作空间中存在。

  • action_args (torch.Tensor): 连续动作参数，仅在混合动作空间中存在。

Returns:

  • 输出 (Dict[str, torch.Tensor]): QAC前向计算图的输出字典，包括 q_value。

ReturnKeys:

  • q_value (torch.Tensor): Q值张量，大小与批量大小相同。

Shapes:

  • obs (torch.Tensor): \((B, N1)\), 其中 B 是批量大小，N1 是 obs_shape。

  • logit (torch.Tensor): \((B, N2)\), B 是批量大小，N2 对应于 action_shape.action_type_shape。

  • action_args (torch.Tensor): \((B, N3)\), B 是批量大小，N3 对应于 action_shape.action_args_shape。

  • 动作 (torch.Tensor): \((B, N4)\), 其中 B 是批量大小，N4 是 action_shape。

  • q_value (torch.Tensor): \((B, )\), 其中 B 是批量大小。

Examples:
>>> inputs = {'obs': torch.randn(4, 8), 'action': torch.randn(4, 1)}
>>> model = ContinuousQAC(obs_shape=(8, ),action_shape=1, action_space='regression')
>>> assert model(inputs, mode='compute_critic')['q_value'].shape == (4, )  # q value
forward(inputs: Tensor | Dict[str, Tensor], mode: str) → Dict[str, Tensor][来源]
Overview:

QAC前向计算图，输入观测张量以预测Q值或动作逻辑值。不同的mode将使用不同的网络模块进行前向传播，以获得不同的输出并节省计算。

Arguments:

  • 输入 (Union[torch.Tensor, Dict[str, torch.Tensor]]): 用于前向计算图的输入数据，对于 compute_actor，它是观察张量，对于 compute_critic，它是包含观察和动作张量的字典数据。

  • 模式 (str): 前向模式，所有模式都在这个类的开头定义。

Returns:

  • 输出 (Dict[str, torch.Tensor]): QAC前向计算图的输出字典，其键值在不同的前向模式中有所不同。

Examples (Actor):
>>> # Regression mode
>>> model = ContinuousQAC(64, 6, 'regression')
>>> obs = torch.randn(4, 64)
>>> actor_outputs = model(obs,'compute_actor')
>>> assert actor_outputs['action'].shape == torch.Size([4, 6])
>>> # Reparameterization Mode
>>> model = ContinuousQAC(64, 6, 'reparameterization')
>>> obs = torch.randn(4, 64)
>>> actor_outputs = model(obs,'compute_actor')
>>> assert actor_outputs['logit'][0].shape == torch.Size([4, 6])  # mu
>>> actor_outputs['logit'][1].shape == torch.Size([4, 6]) # sigma
Examples (Critic):
>>> inputs = {'obs': torch.randn(4, 8), 'action': torch.randn(4, 1)}
>>> model = ContinuousQAC(obs_shape=(8, ),action_shape=1, action_space='regression')
>>> assert model(inputs, mode='compute_critic')['q_value'].shape == (4, )  # q value

训练 actor-critic 模型

首先，我们在 _init_learn 中分别初始化 actor 和 critic 优化器。 设置两个独立的优化器可以保证我们在计算 actor 损失时只更新 actor 网络参数而不更新 critic 网络，反之亦然。

# actor and critic optimizer
self._optimizer_actor = Adam(
    self._model.actor.parameters(),
    lr=self._cfg.learn.learning_rate_actor,
    weight_decay=self._cfg.learn.weight_decay
)
self._optimizer_critic = Adam(
    self._model.critic.parameters(),
    lr=self._cfg.learn.learning_rate_critic,
    weight_decay=self._cfg.learn.weight_decay
)
在 _forward_learn 中，我们通过计算 critic 损失、更新 critic 网络、计算 actor 损失和更新 actor 网络来更新 actor-critic 策略。

  1. critic loss computation

    • 计算当前值和目标值

    # current q value
q_value = self._learn_model.forward(data, mode='compute_critic')['q_value']
# target q value. SARSA: first predict next action, then calculate next q value
with torch.no_grad():
    next_action = self._target_model.forward(next_obs, mode='compute_actor')['action']
    next_data = {'obs': next_obs, 'action': next_action}
    target_q_value = self._target_model.forward(next_data, mode='compute_critic')['q_value']

    • 计算损失

    # DDPG: single critic network
td_data = v_1step_td_data(q_value, target_q_value, reward, data['done'], data['weight'])
critic_loss, td_error_per_sample = v_1step_td_error(td_data, self._gamma)
loss_dict['critic_loss'] = critic_loss

  2. critic network update

self._optimizer_critic.zero_grad()
loss_dict['critic_loss'].backward()
self._optimizer_critic.step()

  1. actor loss

actor_data = self._learn_model.forward(data['obs'], mode='compute_actor')
actor_data['obs'] = data['obs']
actor_loss = -self._learn_model.forward(actor_data, mode='compute_critic')['q_value'].mean()
loss_dict['actor_loss'] = actor_loss

  1. actor network update

# actor update
self._optimizer_actor.zero_grad()
actor_loss.backward()
self._optimizer_actor.step()

目标网络

我们通过 _init_learn 中的目标模型初始化来实现目标网络。 我们配置 learn.target_theta 来控制平均中的插值因子。

# main and target models
self._target_model = copy.deepcopy(self._model)
self._target_model = model_wrap(
    self._target_model,
    wrapper_name='target',
    update_type='momentum',
    update_kwargs={'theta': self._cfg.learn.target_theta}
)

基准

环境

最佳平均奖励

评估结果

配置链接

比较

半猎豹

(HalfCheetah-v3)

11334

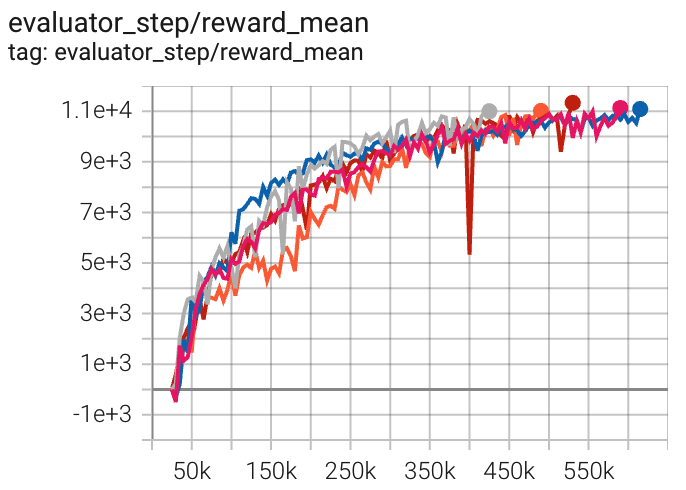
 ../_images/halfcheetah_ddpg.png

config_link_p

Tianshou(11719) Spinning-up(11000)

霍珀

(Hopper-v2)

3516

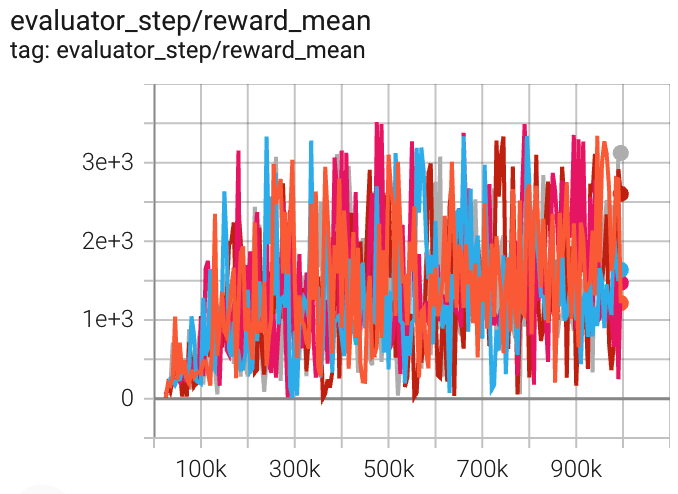
 ../_images/hopper_ddpg.png

config_link_q

天授(2197) 旋转(1800)

Walker2d

(Walker2d-v2)

3443

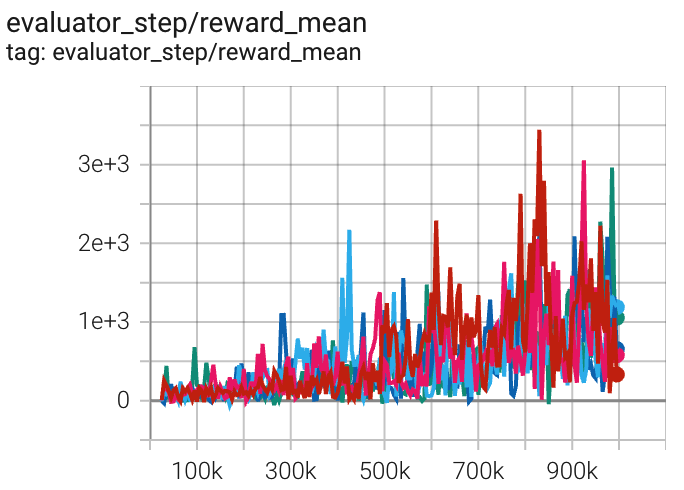
 ../_images/walker2d_ddpg.png

config_link_s

天授(1401) 旋转(1950)

附注：

  1. 上述结果是通过在五个不同的随机种子(0,1,2,3,4)上运行相同的配置获得的。

参考

Timothy P. Lillicrap, Jonathan J. Hunt, Alexander Pritzel, Nicolas Heess, Tom Erez, Yuval Tassa, David Silver, Daan Wierstra: “使用深度强化学习的连续控制”, 2015; [http://arxiv.org/abs/1509.02971 arXiv:1509.02971].

David Silver, Guy Lever, Nicolas Heess, Thomas Degris, Daan Wierstra, 等人。确定性策略梯度算法。ICML，2014年6月，中国北京。ffhal-00938992f

Hafner, R., Riedmiller, M. 反馈控制中的强化学习。Mach Learn 84, 137–169 (2011).

Degris, T., White, M., 和 Sutton, R. S. (2012b). 线性离策略演员-评论家. 在第29届国际机器学习会议上.

其他公开的实现