扩散器（平面扩散器）¶

概述¶

在强化学习领域，如果我们有一个包含各种轨迹的数据集\(T\)，强化学习的目标是从\(T\)中挖掘并构建一个高性能的代理，希望它可以直接部署到环境中并取得良好的回报。从无模型离线强化学习的角度来看，工作的核心集中在如何更准确地估计每个可能的状态-动作对的\(Q\)值，特别是那些可能查询分布外状态-动作对的情况。从基于模型的离线强化学习的角度来看，目标通常变成如何更好地用这批数据拟合真实环境的动态模型，然后在这个收敛的环境模型上实施在线强化学习算法。在这两种算法完成后，我们通常会得到一个显式或隐式的策略，该策略可以在给定任何环境状态的情况下返回与环境交互的动作。

上述方法通常没有利用轨迹在\(T\)中的连续性，而是将每条轨迹划分为几个状态转换段，并将每个这样的段视为后续训练的独立样本点。然而，我们可以从一个全新的角度来看待这个数据集\(T\)，将整个轨迹视为一个样本点，从而将我们的目标改变为对整个轨迹的分布进行建模。最终，我们可以从分布中采样轨迹，以轨迹最优性作为条件变量。

近年来，扩散模型在生成领域表现出色。与其他生成模型（如VAE和GAN）相比，扩散模型在建模复杂分布方面具有更强的能力。因此，研究人员考虑尝试使用扩散模型来建模 \(T\)中的轨迹分布。扩散，如研究Planning with Diffusion for Flexible Behavior Synthesis中所提出的，代表了一种使用扩散模型生成轨迹的研究方法。

快速事实¶

扩散视图将离线决策视为一个序列模型问题。
扩散使用扩散模型生成轨迹

关键方程或关键图表¶

在扩散过程中，轨迹在数组中按以下方式连接：

\[\begin{split}\begin{align} \tau = \begin{bmatrix}s_0 s_1 ... s_T\\a_0 a_1 ... a_T \end{bmatrix} \nonumber\end{align}\end{split}\]

关于轨迹中每次转换之间的时间依赖性，Diffusion 并不强调自回归或马尔可夫性质，而是对时间局部性做出了更为宽松的假设。Diffusion 通过迭代去噪状态-动作对来采样计划中的轨迹，这些状态-动作对具有可变的量。在单个去噪步骤中，较小的感受野限制了模型基于轨迹中的相邻帧推断去噪结果。

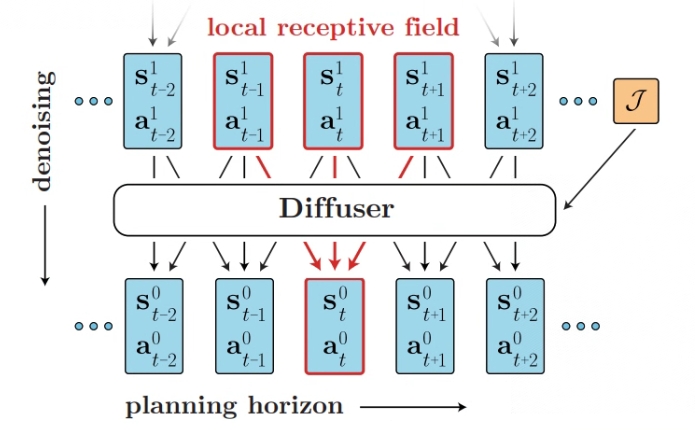
原始论文使用了一个由重复的（时间）卷积残差块组成的模型来满足这些标准。最终结构主要借鉴了图像扩散模型中常用的U-Nets，但将二维空间卷积替换为一维时间卷积。该模型的损失函数为：

\[\mathcal{L}(\theta) = \mathbb{E}_{i, \epsilon, \tau^0}[||\epsilon - \epsilon_\theta(\tau^i, i)||^2]\nonumber\]

该算法将强化学习问题转化为条件采样问题。它利用一个引导函数来评估每个样本轨迹在每一个时间步t的值。最终，算法选择最佳轨迹作为其输出。最佳轨迹如下：

\[p(\mathcal{O}_t = 1) = exp(r(s_t, a_t))\]

\[\begin{align} p(\tau| \mathcal{O}_{1:T} = 1) \propto p(\tau)p(\mathcal{O}_{1:T} = 1|\tau) \nonumber \end{align}\]

实现¶

默认配置定义如下：

class ding.policy.plan_diffuser.PDPolicy(cfg: EasyDict, model: Module | None = None, enable_field: List[str] | None = None)[source]

Overview:
隐式计划扩散器 https://arxiv.org/pdf/2205.09991.pdf

使用的网络接口扩散定义如下：

class ding.model.template.diffusion.GaussianDiffusion(model: str, model_cfg: dict, horizon: int, obs_dim: int | SequenceType, action_dim: int | SequenceType, n_timesteps: int = 1000, predict_epsilon: bool = True, loss_discount: float = 1.0, clip_denoised: bool = False, action_weight: float = 1.0, loss_weights: dict | None = None)[来源]

Overview:
高斯扩散模型

Arguments:

模型 (str): 模型的类型

model_cfg (:obj:’dict’) 模型的配置

horizon (int): 轨迹的horizon

obs_dim (int): 观测的维度

action_dim (int): 动作的维度

n_timesteps (int): 时间步数

predict_epsilon (:obj:’bool’): 是否预测epsilon

loss_discount (:obj:’float’): 损失折扣

clip_denoised (:obj:’bool’): 是否使用 clip_denoised

action_weight (:obj:’float’): 动作的权重

loss_weights (:obj:’dict’): 损失权重

forward(cond, *args, **kwargs)[source]

定义每次调用时执行的计算。

应该由所有子类覆盖。

注意

尽管前向传递的配方需要在此函数内定义，但之后应该调用Module实例而不是这个，因为前者负责运行已注册的钩子，而后者则默默地忽略它们。

基准测试¶

Benchmark and comparison of DT algorithm¶
环境	奖励均值	配置链接	比较
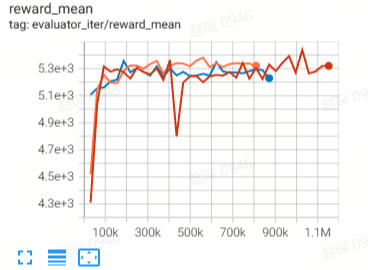
Halfcheetah (Halfcheetah-medium-v2)	44.9	config_link_1	42.8
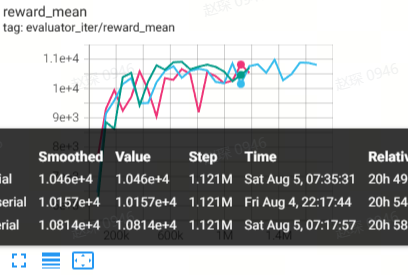
Halfcheetah (Halfcheetah-medium-expert-v2)	86.6	config_link_2	88.9
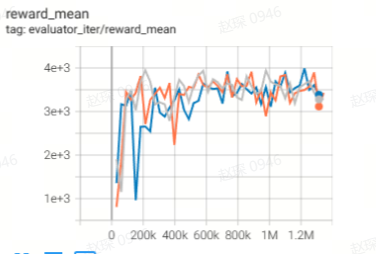
Walker2d (Walker2d-medium-v2)	71	config_link_3	79.6
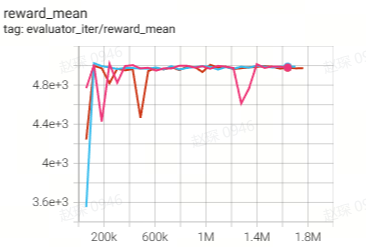
Walker2d (Walker2d-medium-expert-v2)	108.5	config_link_4	106.9
Hopper (Hopper-medium-v2)	58.1	config_link_5	74.3
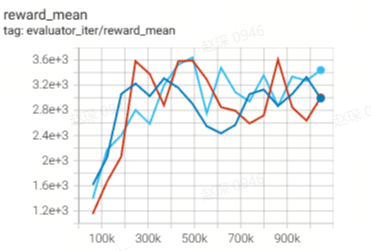
Hopper (Hopper-medium-expert-v2)	97.2	config_link_6	103.3