Table of Contents
Shortcuts

FQF

概述

FQF 首次在论文 Fully Parameterized Quantile Function for Distributional Reinforcement Learning 中被提出。 FQF 和 IQN (Implicit Quantile Networks for Distributional Reinforcement Learning) 的主要区别在于，FQF 额外引入了 the fraction proposal network，这是一个被训练的参数函数，用于在[0, 1]范围内生成 tau, 而 IQN 是从一个 base distribution, 如 U([0, 1]) 对 tau 进行采样。

核心要点

  1. FQF 是一种 无模型（model-free） and 基于值（value-based） 的值分布强化学习算法。

  2. FQF 仅支持 离散动作空间 。

  3. FQF 是一种 异策略（off-policy） 算法。

  4. 通常情况下， FQF 使用 eps-greedy 或 多项式采样（multinomial sample） 进行探索。

  5. FQF 可以与循环神经网络 (RNN) 结合使用。

关键方程或关键框图

对于任何非递减的连续 quantile function \(F_{Z}^{-1}\) , 定义 \(F_{Z}^{-1}\) 与 \(F_{Z}^{-1, \tau}\) 的 1-Wasserstein loss 为：

\[W_{1}(Z, \tau)=\sum_{i=0}^{N-1} \int_{\tau_{i}}^{\tau_{i+1}}\left|F_{Z}^{-1}(\omega)-F_{Z}^{-1}\left(\hat{\tau}_{i}\right)\right| d \omega\]

注意由于 \(W_{1}\) 无法被计算出来, 我们不能直接对 the fraction proposal network 进行梯度下降。 取而代之地, 我们把 \(\frac{\partial W_{1}}{\partial \tau_{i}}\) 作为损失函数交给优化器去优化。

\(\frac{\partial W_{1}}{\partial \tau_{i}}\) 由下式计算：

\[\frac{\partial W_{1}}{\partial \tau_{i}}=2 F_{Z}^{-1}\left(\tau_{i}\right)-F_{Z}^{-1}\left(\hat{\tau}_{i}\right)-F_{Z}^{-1}\left(\hat{\tau}_{i-1}\right), \forall i \in(0, N).\]

类似 implicit quantile networks, quantile tau 通过下式被编码进一个 embedding 向量：

\[\phi_{j}(\tau):=\operatorname{ReLU}\left(\sum_{i=0}^{n-1} \cos (\pi i \tau) w_{i j}+b_{j}\right)\]

然后将 the quantile embedding 与环境观测的 embedding 进行元素相乘，随后的全连接层将得到的乘积向量映射到相应的 quantile value 。

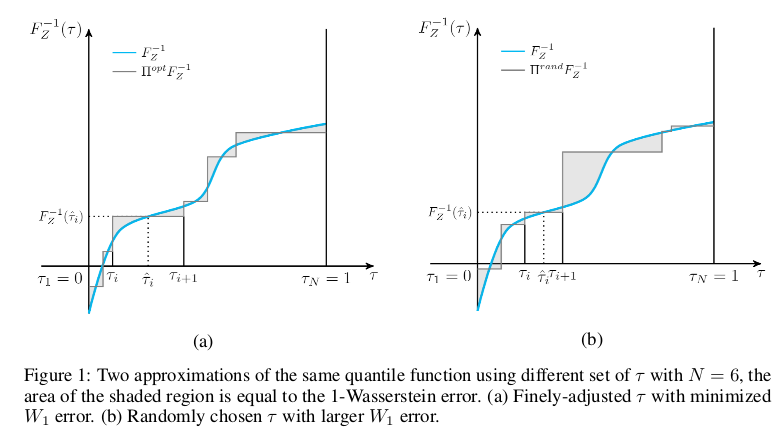
FQF 比 IQN 的优势如下图所示：左图 (a) 是 FQF 通过学习得到的 tau ，右图 (b) 是 IQN 随机选择的 tau ，阴影部分面积即为 1-Wasserstein loss，可以看出 FQF 得到 tau 的方式要比 IQN 得到 tau 的方式产生的 1-Wasserstein loss 要小。

../_images/fqf_iqn_compare.png

伪代码

../_images/FQF.png

扩展

FQF 可以与以下技术相结合使用:

  • 优先经验回放 (Prioritized Experience Replay)

    提示

    是否优先级经验回放 (PER) 能够提升 FQF 的性能取决于任务和训练策略。

  • 多步时序差分 (TD) 损失

  • 双目标网络 (Double Target Network)

  • 循环神经网络 (RNN)

实现

提示

我们的 FQF 基准结果使用与DQN相同的超参数，除了 FQF 的独有超参数， the number of quantiles， 它经验性地设置为32。直观地说，与随机 fractions 相比，trained quantile fractions 的优势在较小的 N 下更容易被观察到。在较大的 N 下，当 trained quantile fractions 和随机 fractions 都密集地分布在[0, 1]时， FQF 和 IQN 之间的差异变得可以忽略不计。

FQF 算法的默认配置如下所示：

class ding.policy.fqf.FQFPolicy(cfg: EasyDict, model: Module | None = None, enable_field: List[str] | None = None)[source]
Overview:

FQF（全参数化分位数函数）算法的策略类，提出于 https://arxiv.org/pdf/1911.02140.pdf。

Config:

ID

符号

类型

默认值

描述

其他（形状）

1

type

字符串

fqf
RL policy register name, refer to
registry POLICY_REGISTRY
this arg is optional,
a placeholder

2

cuda

布尔

假
Whether to use cuda for network
this arg can be diff-
erent from modes

3

on_policy

布尔

假
Whether the RL algorithm is on-policy
or off-policy

4

priority

布尔

真
Whether use priority(PER)
priority sample,
update priority

6
other.eps
.start

浮点数

0.05
Start value for epsilon decay. It’s
small because rainbow use noisy net.

7
other.eps
.end

浮点数

0.05
End value for epsilon decay.

8
discount_
factor

浮点数

0.97, [0.95, 0.999]
Reward’s future discount factor, aka.
gamma
may be 1 when sparse
reward env

9

nstep

整数

3, [3, 5]
N-step reward discount sum for target
q_value estimation

10
learn.update
per_collect

整数

3
How many updates(iterations) to train
after collector’s one collection. Only
valid in serial training
this args can be vary
from envs. Bigger val
means more off-policy

11

learn.kappa

浮点数

/
Threshold of Huber loss

FQF 算法使用的网络接口定义如下：

class ding.model.template.q_learning.FQF(obs_shape: int | SequenceType, action_shape: int | SequenceType, encoder_hidden_size_list: SequenceType = [128, 128, 64], head_hidden_size: int | None = None, head_layer_num: int = 1, num_quantiles: int = 32, quantile_embedding_size: int = 128, activation: Module | None = ReLU(), norm_type: str | None = None)[source]
Overview:

FQF的神经网络结构和计算图，结合了分布强化学习和DQN。您可以参考论文《完全参数化的分位数函数用于分布强化学习》https://arxiv.org/pdf/1911.02140.pdf了解更多详情。

Interface:

__init__, forward

forward(x: Tensor) → Dict[源代码]
Overview:

使用编码的嵌入张量来预测FQF的输出。 参数更新使用FQF的MLPs前向设置。

Arguments:
  • x (torch.Tensor):

    编码后的嵌入张量，形状为 (B, N=hidden_size)。

Returns:

  • 输出 (Dict): 包含关键词 logit (torch.Tensor), q (torch.Tensor), quantiles (torch.Tensor), quantiles_hats (torch.Tensor), q_tau_i (torch.Tensor), entropies (torch.Tensor) 的字典。

Shapes:

  • x: \((B, N)\), 其中 B 是批量大小，N 是 head_hidden_size。

  • logit: \((B, M)\), 其中 M 是 action_shape。

  • q: \((B, num_quantiles, M)\).

  • 分位数: \((B, num_quantiles + 1)\).

  • quantiles_hats: \((B, num_quantiles)\).

  • q_tau_i: \((B, num_quantiles - 1, M)\).

  • 熵值: \((B, 1)\).

Examples:
>>> model = FQF(64, 64) # arguments: 'obs_shape' and 'action_shape'
>>> inputs = torch.randn(4, 64)
>>> outputs = model(inputs)
>>> assert isinstance(outputs, dict)
>>> assert outputs['logit'].shape == torch.Size([4, 64])
>>> # default num_quantiles: int = 32
>>> assert outputs['q'].shape == torch.Size([4, 32, 64])
>>> assert outputs['quantiles'].shape == torch.Size([4, 33])
>>> assert outputs['quantiles_hats'].shape == torch.Size([4, 32])
>>> assert outputs['q_tau_i'].shape == torch.Size([4, 31, 64])
>>> assert outputs['quantiles'].shape == torch.Size([4, 1])

FQF 算法中使用的贝尔曼更新（Bellman update）在 fqf_nstep_td_error 函数中定义，我们可以在 ding/rl_utils/td.py 文件中找到它。

基准测试

环境

最佳平均奖励

评估结果

配置链接

比较

乒乓球

(PongNoFrameskip-v4)

21

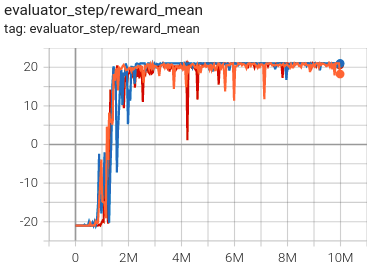
 ../_images/FQF_pong.png

config_link_p

Tianshou(20.7)

Qbert

(QbertNoFrameskip-v4)

23416

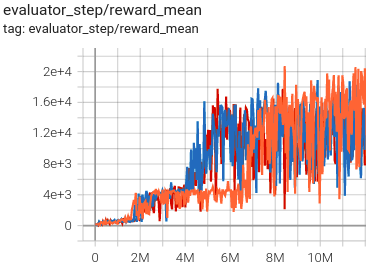
 ../_images/FQF_qbert.png

config_link_q

Tianshou(16172.5)

太空侵略者

(SpaceInvadersNoFrame skip-v4)

2727.5

 ../_images/FQF_spaceinvaders.png

config_link_s

天寿(2482)
P.S.:

  1. 上述结果是通过在三个不同的随机种子 (0, 1, 2) 上运行相同的配置获得的。

参考文献

(FQF) Derek Yang, Li Zhao, Zichuan Lin, Tao Qin, Jiang Bian, Tieyan Liu: “完全参数化的分位数函数用于分布强化学习”, 2019; arXiv:1911.02140. https://arxiv.org/pdf/1911.02140

其他开源实现