IQN¶
概述¶
IQN 是在 Implicit Quantile Networks for Distributional Reinforcement Learning 被提出的。 Distributional RL 的研究目标是通过建模值函数的概率分布,更全面地描述不同动作的预期奖励分布。 IQN (Implicit Quantile Network)和 QRDQN (Quantile Regression DQN) 之间的关键区别在于, IQN 引入了隐式量化网络(Implicit Quantile Network),它是一个确定性参数化函数,通过训练将来自基本分布(例如在U([0, 1])上的 tau )的样本重新参数化为目标分布的相应分位数值,而 QRDQN 直接学习了一组预定义的固定分位数。
要点摘要:¶
IQN 是一种 无模型(model-free) 和 基于值(value-based) 的强化学习算法。
IQN 仅支持 离散动作空间 。
IQN 是一种 异策略(off-policy) 算法。
通常情况下, IQN 使用 eps-greedy 或 多项式采样(multinomial sample) 进行探索。
IQN 可以与循环神经网络 (RNN) 结合使用。
关键方程¶
在隐式量化网络中,首先通过以下方式将采样的分位数tau编码为嵌入向量:
\[\phi_{j}(\tau):=\operatorname{ReLU}\left(\sum_{i=0}^{n-1} \cos (\pi i \tau) w_{i j}+b_{j}\right)\]
然后,分位数嵌入(quantile embedding)与环境观测的嵌入(embedding)进行逐元素相乘,并通过后续的全连接层将得到的乘积向量映射到相应的分位数值。
关键图¶
以下是DQN、C51、QRDQN和IQN之间的比较:
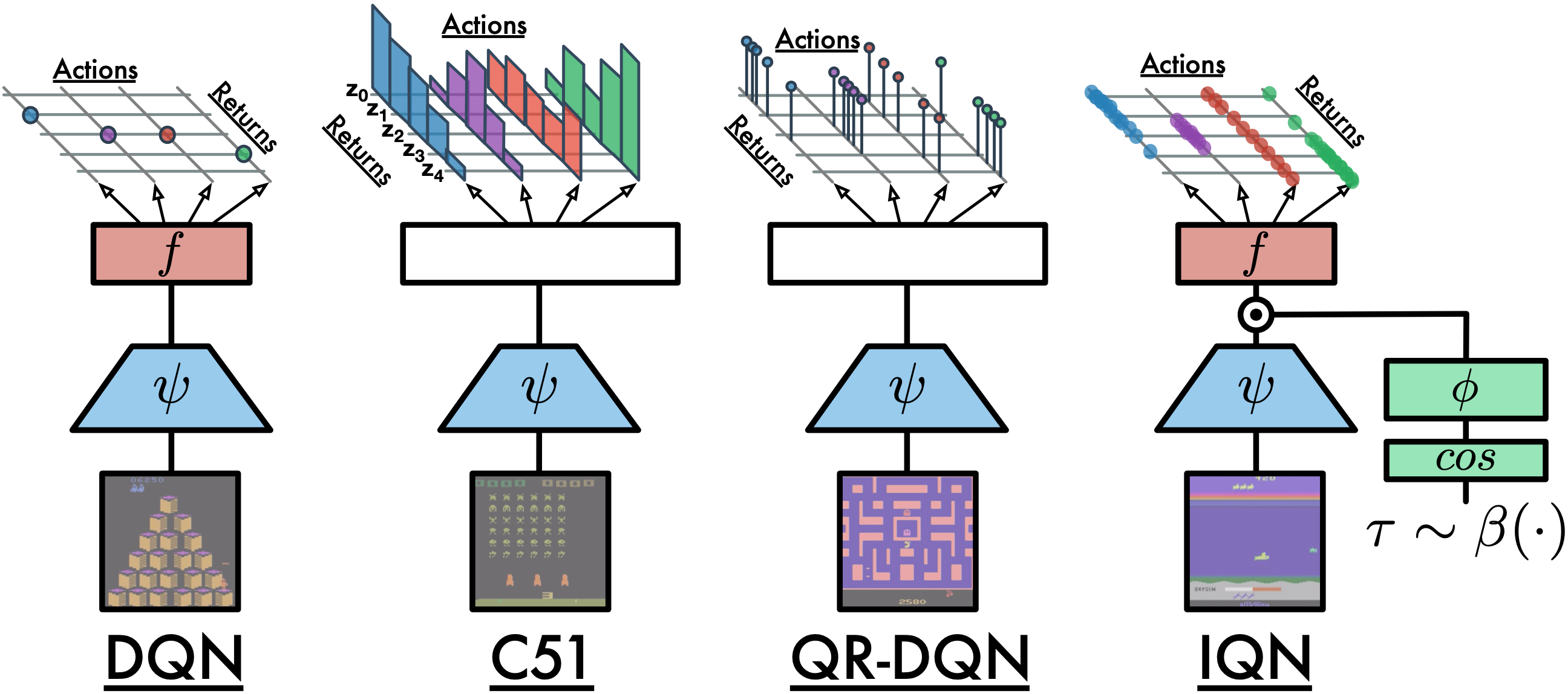
扩展¶
- IQN 可以与以下技术相结合使用:
优先经验回放 (Prioritized Experience Replay)
提示
是否优先级经验回放 (PER) 能够提升 IQN 的性能取决于任务和训练策略。
多步时序差分 (TD) 损失
双目标网络 (Double Target Network)
循环神经网络 (RNN)
实现¶
提示
我们的IQN基准结果使用与DQN相同的超参数,除了IQN的独有超参数, the number of quantiles, 它经验性地设置为32。不推荐将分位数的数量设置为大于64,因为这会带来较小的收益,并且会增加更多的前向传递延迟。
IQN算法的默认配置如下所示:
- class ding.policy.iqn.IQNPolicy(cfg: EasyDict, model: Module | None = None, enable_field: List[str] | None = None)[source]
- Overview:
IQN算法的策略类。论文链接:https://arxiv.org/pdf/1806.06923.pdf。分布式强化学习是强化学习的一个新方向,比传统的强化学习算法更稳定。分布式强化学习的核心思想是估计动作值的分布,而不是期望值。IQN和DQN的区别在于,IQN使用分位数回归来估计动作分布的分位数值,而DQN使用动作分布的期望值。
- Config:
ID
符号
类型
默认值
描述
其他(形状)
1
type字符串
qrdqn
RL policy register name, refer toregistryPOLICY_REGISTRYthis arg is optional,a placeholder2
cuda布尔
假
Whether to use cuda for networkthis arg can be diff-erent from modes3
on_policy布尔
假
Whether the RL algorithm is on-policyor off-policy4
priority布尔
真
Whether use priority(PER)priority sample,update priority6
other.eps.start浮点数
0.05
Start value for epsilon decay. It’ssmall because rainbow use noisy net.7
other.eps.end浮点数
0.05
End value for epsilon decay.8
discount_factor浮点数
0.97, [0.95, 0.999]
Reward’s future discount factor, aka.gammamay be 1 when sparsereward env9
nstep整数
3, [3, 5]
N-step reward discount sum for targetq_value estimation10
learn.updateper_collect整数
3
How many updates(iterations) to trainafter collector’s one collection. Onlyvalid in serial trainingthis args can be varyfrom envs. Bigger valmeans more off-policy11
learn.kappa浮点数
/
Threshold of Huber loss
IQN算法使用的网络接口定义如下:
- class ding.model.template.q_learning.IQN(obs_shape: int | SequenceType, action_shape: int | SequenceType, encoder_hidden_size_list: SequenceType = [128, 128, 64], head_hidden_size: int | None = None, head_layer_num: int = 1, num_quantiles: int = 32, quantile_embedding_size: int = 128, activation: Module | None = ReLU(), norm_type: str | None = None)[source]
- Overview:
IQN的神经网络结构和计算图,结合了分布强化学习和DQN。您可以参考论文《隐式分位数网络用于分布强化学习》https://arxiv.org/pdf/1806.06923.pdf了解更多详情。
- Interfaces:
__init__,forward
- forward(x: Tensor) Dict[来源]
- Overview:
使用编码的嵌入张量来预测IQN的输出。 通过IQN的MLPs前向设置进行参数更新。
- Arguments:
- x (
torch.Tensor): 编码后的嵌入张量,形状为
(B, N=hidden_size)。
- x (
- Returns:
- outputs (
Dict): 使用编码器和头部运行。返回结果预测字典。
- outputs (
- ReturnsKeys:
logit (
torch.Tensor): 与输入x大小相同的 Logit 张量。q (
torch.Tensor): Q 值张量,大小为(num_quantiles, N, B)分位数 (
torch.Tensor): 大小为(quantile_embedding_size, 1)的分位数张量
- Shapes:
x (
torch.Tensor): \((B, N)\), 其中 B 是批量大小,N 是 head_hidden_size。logit (
torch.FloatTensor): \((B, M)\), 其中 M 是 action_shape分位数 (
torch.Tensor): \((P, 1)\), 其中 P 是分位数嵌入大小。
- Examples:
>>> model = IQN(64, 64) # arguments: 'obs_shape' and 'action_shape' >>> inputs = torch.randn(4, 64) >>> outputs = model(inputs) >>> assert isinstance(outputs, dict) >>> assert outputs['logit'].shape == torch.Size([4, 64]) >>> # default num_quantiles: int = 32 >>> assert outputs['q'].shape == torch.Size([32, 4, 64] >>> # default quantile_embedding_size: int = 128 >>> assert outputs['quantiles'].shape == torch.Size([128, 1])
IQN算法中使用的贝尔曼更新(Bellman update)在 iqn_nstep_td_error 函数中定义,我们可以在 ding/rl_utils/td.py 文件中找到它。
基准¶
环境 |
最佳平均奖励 |
评估结果 |
配置链接 |
比较 |
|---|---|---|---|---|
乒乓球 (PongNoFrameskip-v4) |
20 |
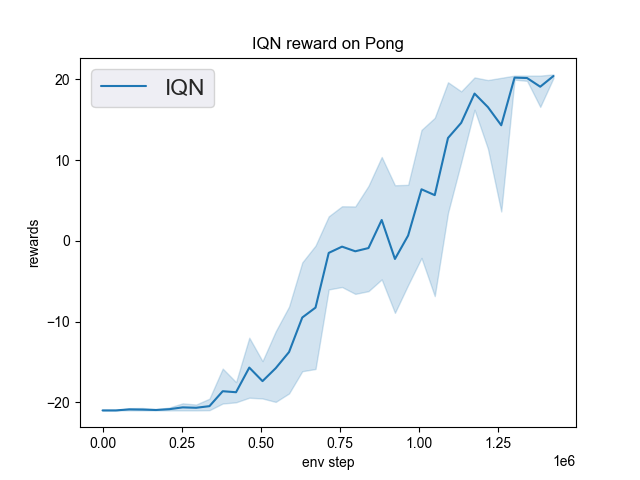
|
Tianshou(20) |
|
Qbert (QbertNoFrameskip-v4) |
16331 |

|
Tianshou(15520) |
|
太空侵略者 (SpaceInvadersNoFrame skip-v4) |
1493 |
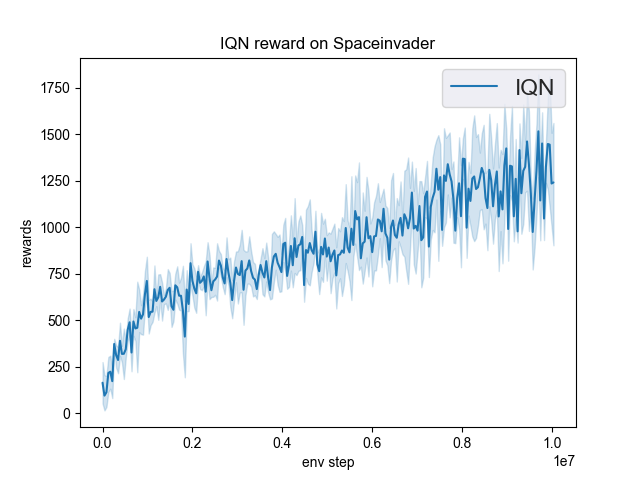
|
Tianshou(1370) |
P.S.: 1. 上述结果是通过在五个不同的随机种子 (0, 1, 2, 3, 4)上运行相同的配置获得的。
参考文献¶
(IQN) Will Dabney, Georg Ostrovski, David Silver, Rémi Munos: “用于分布式强化学习的隐式分位数网络”, 2018; arXiv:1806.06923. https://arxiv.org/pdf/1806.06923