SAC¶

概述¶

软演员-评论家（SAC）是一种稳定且高效的无模型离策略最大熵演员-评论家算法，适用于连续状态和动作空间，该算法在2018年的论文软演员-评论家：具有随机演员的离策略最大熵深度强化学习中提出。策略的增强熵目标带来了许多概念和实践上的优势，包括更强大的探索能力和策略捕捉接近最优行为的多种模式的能力。作者还展示了这种方法通过将离策略更新与稳定的随机演员-评论家公式相结合，在一系列连续控制基准任务上实现了最先进的性能，优于之前的在策略和离策略方法。

快速事实¶

SAC 是为具有连续动作空间的环境实现的。（例如 MuJoCo、Pendulum 和 LunarLander）
SAC 是一种 离策略 和 无模型 的算法，结合非空回放缓冲区进行策略探索。
SAC是一种actor-critic强化学习算法，它分别优化了actor网络和critic网络，
SAC 也适用于多连续动作空间。

关键方程或关键图表¶

SAC考虑了一个更一般的最大熵目标，通过增加策略的期望熵来增强目标，从而倾向于随机策略：

\[J(\pi)=\sum_{t=0}^{T} \mathbb{E}_{\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right) \sim \rho_{\pi}}\left[r\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)+\alpha \mathcal{H}\left(\pi\left(\cdot \mid \mathbf{s}_{t}\right)\right)\right].\]

温度参数 \(\alpha > 0\) 控制最优策略的随机性。

Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor 考虑了一个参数化的状态值函数、软Q函数和一个易于处理的策略。具体来说，值函数和软Q函数被建模为表达性神经网络，而策略则被建模为由神经网络给出的均值和协方差的高斯分布。特别是，SAC应用了重参数化技巧，而不是直接最小化策略参数的期望KL散度，如下所示：

\[J_{\pi}(\phi)=\mathbb{E}_{\mathbf{s}_{t} \sim \mathcal{D}, \epsilon_{t} \sim \mathcal{N}}\left[\log \pi_{\phi}\left(f_{\phi}\left(\epsilon_{t} ; \mathbf{s}_{t}\right) \mid \mathbf{s}_{t}\right)-Q_{\theta}\left(\mathbf{s}_{t}, f_{\phi}\left(\epsilon_{t} ; \mathbf{s}_{t}\right)\right)\right]\]

我们通过配置learn.reparameterization来实现重参数化技巧。

注意

与原始版本建模状态值函数和软Q函数相比，我们的实现包含两个版本。一个是建模状态值函数和软Q函数，另一个是通过双网络仅建模软Q函数。

注意

Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor 考虑了一个参数化的状态值函数、软Q函数和一个可处理的策略。我们的实现包含两个版本。一个是建模状态值函数和软Q函数，另一个是通过双网络仅建模软Q函数。我们配置 model.value_network, model.twin_q, 和 learn.learning_rate_value 来切换实现版本。

伪代码¶

注意

与原始版本相比，我们在第二个实现版本中仅优化了q网络和actor网络。

扩展¶

SAC 可以与以下内容结合使用：

自动阿尔法策略

Reinforcement Learning with Deep Energy-Based Policies 提出了熵系数 \(\alpha\) 用于确定熵和奖励的相对重要性。 Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor 进行的广泛实验表明，软演员-评论家对奖励缩放敏感，因为它与最优策略的温度有关。最优奖励缩放因环境而异，应针对每个任务单独调整。由于我们通过配置 learn.is_auto_alpha 和 learn.alpha 实现了基于最大熵的自动 alpha 策略。

实现¶

默认配置定义如下：

class ding.policy.sac.SACPolicy(cfg: EasyDict, model: Module | None = None, enable_field: List[str] | None = None)[source]¶

Overview:

连续SAC算法的策略类。论文链接：https://arxiv.org/pdf/1801.01290.pdf

Config:

ID	符号	类型	默认值	描述	其他
1	`type`	字符串	sac	RL policy register name, refer to registry `POLICY_REGISTRY`	this arg is optional, a placeholder
2	`cuda`	布尔	真	Whether to use cuda for network
3	`on_policy`	布尔	假	SAC is an off-policy algorithm.
4	`priority`	布尔	假	Whether to use priority sampling in buffer.
5	`priority_IS_` `weight`	布尔	假	Whether use Importance Sampling weight to correct biased update
6	`random_` `collect_size`	整数	10000	Number of randomly collected training samples in replay buffer when training starts.	Default to 10000 for SAC, 25000 for DDPG/ TD3.
7	`learn.learning` `_rate_q`	浮点数	3e-4	Learning rate for soft q network.	Defalut to 1e-3
8	`learn.learning` `_rate_policy`	浮点数	3e-4	Learning rate for policy network.	Defalut to 1e-3
9	`learn.alpha`	浮点数	0.2	Entropy regularization coefficient.	alpha is initiali- zation for auto alpha, when auto_alpha is True
10	`learn.` `auto_alpha`	布尔	假	Determine whether to use auto temperature parameter alpha.	Temperature parameter determines the relative importance of the entropy term against the reward.
11	`learn.-` `ignore_done`	布尔	假	Determine whether to ignore done flag.	Use ignore_done only in env like Pendulum
12	`learn.-` `target_theta`	浮点数	0.005	Used for soft update of the target network.	aka. Interpolation factor in polyak aver aging for target networks.

我们以第二个版本的实现（仅预测软Q函数）为例来介绍SAC算法：

基本演员-评论家定义

初始化模型。

# build network
self._policy_net = PolicyNet(self._obs_shape, self._act_shape, self._policy_embedding_size)

self._twin_q = twin_q
if not self._twin_q:
    self._soft_q_net = SoftQNet(self._obs_shape, self._act_shape, self._soft_q_embedding_size)
else:
    self._soft_q_net = nn.ModuleList()
    for i in range(2):
        self._soft_q_net.append(SoftQNet(self._obs_shape, self._act_shape, self._soft_q_embedding_size))

来自软Q网络的软Q预测

def compute_critic_q(self, inputs: Dict[str, torch.Tensor]) -> Dict[str, torch.Tensor]:
    action = inputs['action']
    if len(action.shape) == 1:
        action = action.unsqueeze(1)
    state_action_input = torch.cat([inputs['obs'], action], dim=1)
    q_value = self._soft_q_net_forward(state_action_input)
    return {'q_value': q_value}

从策略网络预测行动

def compute_actor(self, obs: torch.Tensor, deterministic_eval=False, epsilon=1e-6) -> Dict[str, torch.Tensor]:
    mean, log_std = self._policy_net_forward(obs)
    std = log_std.exp()

    # unbounded Gaussian as the action distribution.
    dist = Independent(Normal(mean, std), 1)
    # for reparameterization trick (mean + std * N(0,1))
    if deterministic_eval:
        x = mean
    else:
        x = dist.rsample()
    y = torch.tanh(x)
    action = y

    # epsilon is used to avoid log of zero/negative number.
    y = 1 - y.pow(2) + epsilon
    log_prob = dist.log_prob(x).unsqueeze(-1)
    log_prob = log_prob - torch.log(y).sum(-1, keepdim=True)

    return {'mean': mean, 'log_std': log_std, 'action': action, 'log_prob': log_prob}

注意

SAC 对高斯样本应用可逆的压缩函数，并使用变量变换公式来计算有界动作的可能性。具体来说，我们通过 Independent(Normal(mean, std), 1) 使用无界高斯作为动作分布，这创建了一个与多元正态分布形状相同的对角正态分布。这等同于 log_prob.sum(axis=-1)。然后，动作通过 \(\tanh(\text{mean})\) 进行压缩，动作的对数似然具有简单的形式 \(\log \pi(\mathbf{a} \mid \mathbf{s})=\log \mu(\mathbf{u} \mid \mathbf{s})-\sum_{i=1}^{D} \log \left(1-\tanh ^{2}\left(u_{i}\right)\right)\)。特别是，SAC 中的 std 是从观察中预测的，这与 PPO（可学习参数）和 TD3（启发式参数）不同。

熵正则化强化学习如下

目标q值中的熵。

# target q value. SARSA: first predict next action, then calculate next q value
with torch.no_grad():
    (mu, sigma) = self._learn_model.forward(next_obs, mode='compute_actor')['logit']

    dist = Independent(Normal(mu, sigma), 1)
    pred = dist.rsample()
    next_action = torch.tanh(pred)
    y = 1 - next_action.pow(2) + 1e-6
    # keep dimension for loss computation (usually for action space is 1 env. e.g. pendulum)
    next_log_prob = dist.log_prob(pred).unsqueeze(-1)
    next_log_prob = next_log_prob - torch.log(y).sum(-1, keepdim=True)

    next_data = {'obs': next_obs, 'action': next_action}
    target_q_value = self._target_model.forward(next_data, mode='compute_critic')['q_value']
    # the value of a policy according to the maximum entropy objective
    if self._twin_critic:
        # find min one as target q value
        target_q_value = torch.min(target_q_value[0],
                                   target_q_value[1]) - self._alpha * next_log_prob.squeeze(-1)
    else:
        target_q_value = target_q_value - self._alpha * next_log_prob.squeeze(-1)

软Q值网络更新。

# =================
# q network
# =================
# compute q loss
if self._twin_q:
    q_data0 = v_1step_td_data(q_value[0], target_value, reward, done, data['weight'])
    loss_dict['q_loss'], td_error_per_sample0 = v_1step_td_error(q_data0, self._gamma)
    q_data1 = v_1step_td_data(q_value[1], target_value, reward, done, data['weight'])
    loss_dict['q_twin_loss'], td_error_per_sample1 = v_1step_td_error(q_data1, self._gamma)
    td_error_per_sample = (td_error_per_sample0 + td_error_per_sample1) / 2
else:
    q_data = v_1step_td_data(q_value, target_value, reward, done, data['weight'])
    loss_dict['q_loss'], td_error_per_sample = v_1step_td_error(q_data, self._gamma)

# update q network
self._optimizer_q.zero_grad()
loss_dict['q_loss'].backward()
if self._twin_q:
    loss_dict['q_twin_loss'].backward()
self._optimizer_q.step()

策略损失中的熵。

# compute policy loss
policy_loss = (self._alpha * log_prob - new_q_value.unsqueeze(-1)).mean()

loss_dict['policy_loss'] = policy_loss

# update policy network
self._optimizer_policy.zero_grad()
loss_dict['policy_loss'].backward()
self._optimizer_policy.step()

注意

我们通过\((\text{mean} + \text{std} * \mathcal{N}(0,1))\)实现重参数化技巧。特别是，sigma的梯度反向传播是通过策略损失中的log_prob进行的。

自动阿尔法策略

通过日志操作形状进行Alpha初始化。

if self._cfg.learn.is_auto_alpha:
    self._target_entropy = -np.prod(self._cfg.model.action_shape)
    self._log_alpha = torch.log(torch.tensor([self._cfg.learn.alpha]))
    self._log_alpha = self._log_alpha.to(device='cuda' if self._cuda else 'cpu').requires_grad_()
    self._alpha_optim = torch.optim.Adam([self._log_alpha], lr=self._cfg.learn.learning_rate_alpha)
    self._is_auto_alpha = True
    assert self._log_alpha.shape == torch.Size([1]) and self._log_alpha.requires_grad
    self._alpha = self._log_alpha.detach().exp()

Alpha 更新。

# compute alpha loss
if self._is_auto_alpha:
    log_prob = log_prob.detach() + self._target_entropy
    loss_dict['alpha_loss'] = -(self._log_alpha * log_prob).mean()

    self._alpha_optim.zero_grad()
    loss_dict['alpha_loss'].backward()
    self._alpha_optim.step()
    self._alpha = self._log_alpha.detach().exp()

基准测试¶

环境

最佳平均奖励

评估结果

配置链接

比较

猎豹

(Halfcheetah-v3)

12900

config_link_ha

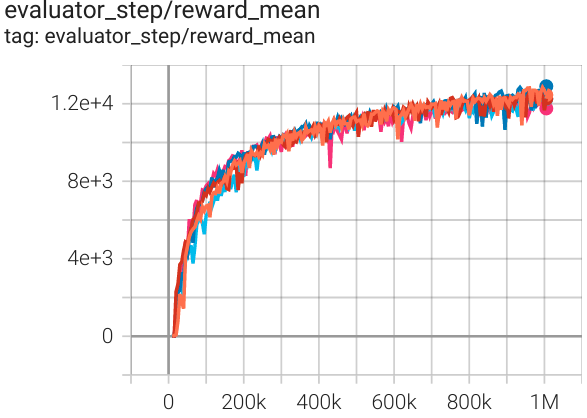
启动中 (13000)

SB3(9535)

Tianshou(12138)

Walker2d

(Walker2d-v2)

5172

config_link_w

启动 (5300)

SB3(3863)

Tianshou(5007)

霍珀

(Hopper-v2)

3653

config_link_ho

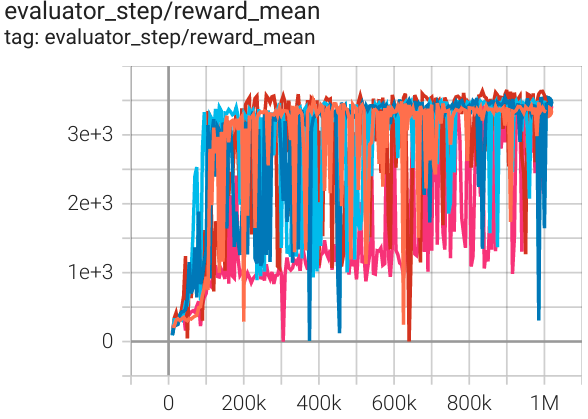
启动中 (3500)

SB3(2325)

天授(3542)

参考¶

Haarnoja等人。软演员-评论家算法及其应用。[https://arxiv.org/abs/1812.05905 arXiv:1812.05905], 2019.
Haarnoja 等人。软性演员-评论家：带有随机演员的离策略最大熵深度强化学习。[https://arxiv.org/abs/1801.01290 arXiv:1801.01290], 2018.