SQIL¶
概述¶
软Q模仿学习(SQIL)是一种结合了模仿学习的离策略最大熵Q学习算法。SQIL首次在SQIL: 通过稀疏奖励的强化学习进行模仿学习中提出,它将软Q学习与模仿学习结合起来。在离散动作空间领域,与深度Q学习算法相比,基于深度能量策略的强化学习中提出的软Q学习学习的是随机(最大熵)策略,而不是确定性策略。
快速事实¶
SQIL 是一种无模型且基于价值的强化学习算法。
SQIL 是将模仿学习融入的 SQL。
SQIL 支持离散和连续动作空间,这与 SQL 相同。
SQIL 是一种 离策略 算法。
在DI-engine中,SQIL使用eps-greedy进行探索。
SQIL的DI-engine实现目前仅支持离散动作空间。
SQIL的优势包括:i. 在面对不确定动态时更具鲁棒性;ii. 自然地结合了探索。
SQIL 可以被视为正则化行为克隆,它在一般行为克隆的基础上具有优势。
关键方程或关键图表¶
SQIL 是 SQL 的一种行为克隆变体,因此您可以先参考 SQL 文档。
SQIL 对 SQL 进行了三个小而重要的修改:
它最初用演示填充代理的经验回放缓冲区,其中奖励设置为常数 r = +1。
当代理与环境交互并积累新的经验时,它会将这些经验添加到回放缓冲区,并将这些新经验的奖励设置为常数 r = 0。
它在每个从回放缓冲区抽取的样本中平衡了示范经验和新经验的数量(各占50%)。
BC 是一种简单的方法,旨在通过监督学习模仿专家的行为——特别是贪婪地最大化给定演示状态下演示行为的条件可能性,而不考虑行为的后果。 理论上,可以证明 SQIL 等同于通过一个正则化项增强 BC,该正则化项将状态转换动态信息纳入模仿策略中,从而实现长期模仿。
具体来说,回顾SQL,软Q值是奖励和动态的函数,由软贝尔曼方程给出:
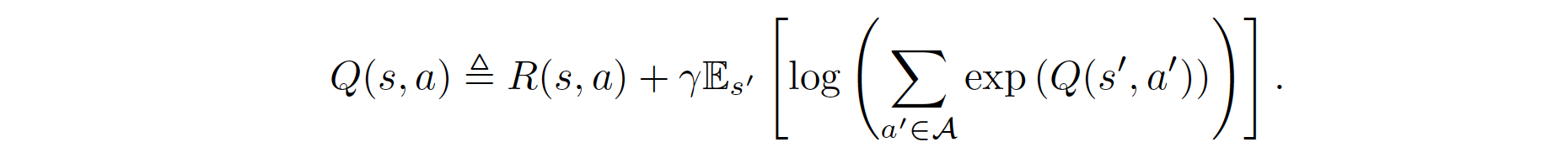
策略 \(\pi\) 形成一个关于动作的玻尔兹曼分布:
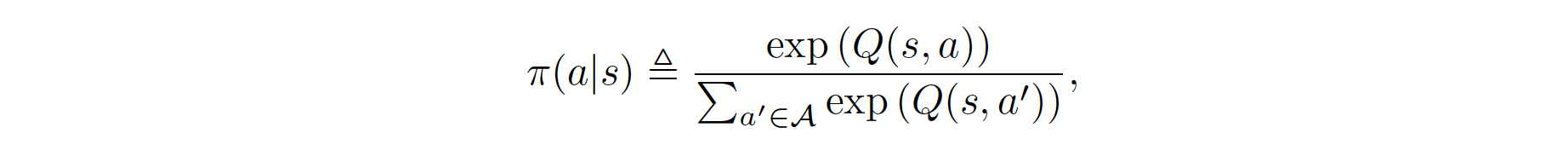
重新排列上述函数,我们得到奖励的公式:
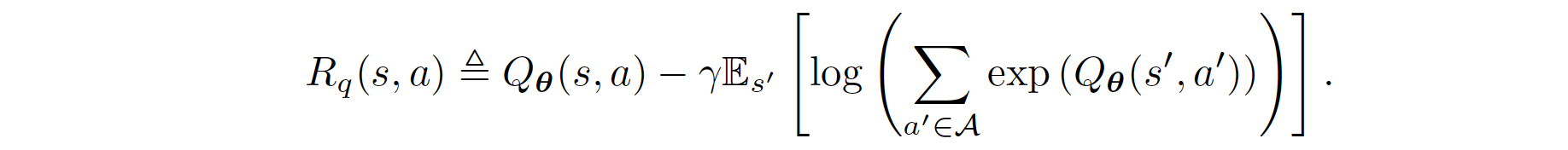
因此,常规的BC可以如下推导:
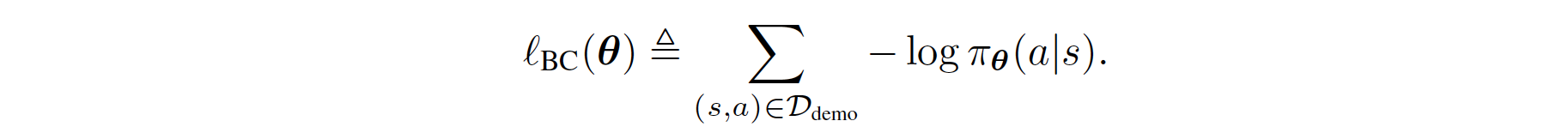

正则化的BC是通过先前的工作Boosted and reward regularized classification for apprenticeship learning制定的,其中Q通过上述奖励的稀疏性先验进行正则化。通过将BC与这种正则化结合,我们最终的正则化BC目标将状态转移动态的信息纳入了模仿学习目标中,因为\(R_{q}(s,a)\)是关于下一个状态\(s'\)的期望函数。正式地,其公式如下:
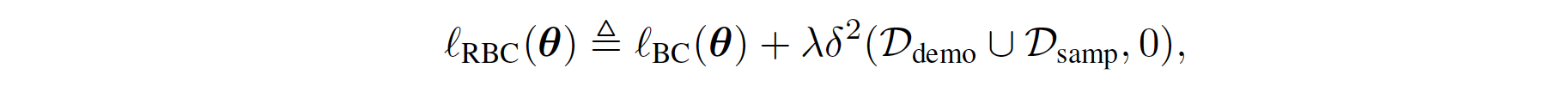
其中 \(\lambda \in \mathbb{R}_{>0}\) 是一个常数超参数,而 \(\delta\) 表示在下面伪代码部分的方程中定义的平方软贝尔曼误差。BC损失鼓励 \(Q\) 在演示状态下的演示动作输出高值,惩罚项将这些高值传播到附近的状态。换句话说,\(Q\) 对于导致从演示状态可达的状态的动作输出高值。因此,当代理发现自己远离演示状态时,它会采取行动使其返回演示状态。
令人惊讶的是,可以证明上述方程中正则化BC损失的梯度与下面算法1第4行中SQIL损失的梯度成正比,再加上一个惩罚初始状态\(s_{0}\)软值的附加项。
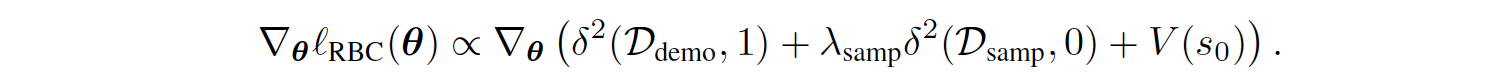
有关完整推导,请参阅原始论文附录中的A.1节。
总之,SQIL 解决了与 Boosted and reward regularized classification for apprenticeship learning 中提出的正则化 BC 类似的优化问题。然而,SQIL 可以被视为一种更实用且简单的方法来实现正则化 BC 的思想。 此外,论文中的实验消融研究表明,SQIL 实际上比正则化 BC 表现更好。
伪代码¶
SQIL = SQL + 模仿学习。伪代码如下:

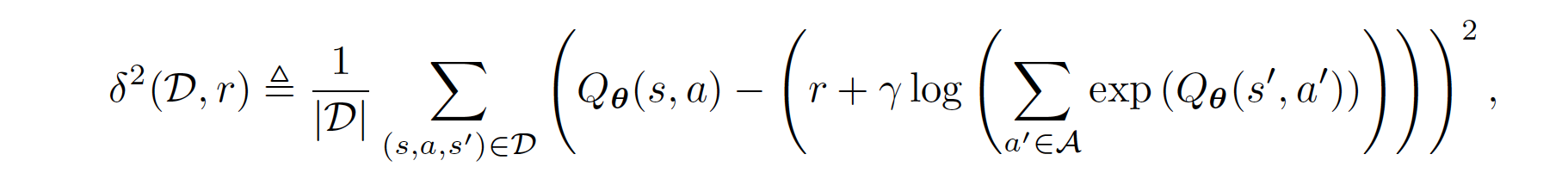
实现¶
默认配置定义如下:
- class ding.policy.sql.SQLPolicy(cfg: EasyDict, model: Module | None = None, enable_field: List[str] | None = None)[source]
- Overview:
SQL算法的策略类。
SQIL/SQL的Bellman更新和Q值函数更新在ding/rl_utils/td.py中的q_nstep_sql_td_error函数中定义:
def q_nstep_sql_td_error(
data: namedtuple,
gamma: float,
alpha: float,
nstep: int = 1,
cum_reward: bool = False,
value_gamma: Optional[torch.Tensor] = None,
criterion: torch.nn.modules = nn.MSELoss(reduction='none'),
) -> torch.Tensor:
"""
Overview:
Multistep (1 step or n step) td_error for q-learning based algorithm
Arguments:
- data (:obj:`q_nstep_td_data`): the input data, q_nstep_sql_td_data to calculate loss
- gamma (:obj:`float`): discount factor
- alpha (:obj:`float`): A parameter to weight entropy term in a policy equation
- cum_reward (:obj:`bool`): whether to use cumulative nstep reward, which is figured out when collecting data
- value_gamma (:obj:`torch.Tensor`): gamma discount value for target soft_q_value
- criterion (:obj:`torch.nn.modules`): loss function criterion
- nstep (:obj:`int`): nstep num, default set to 1
Returns:
- loss (:obj:`torch.Tensor`): nstep td error, 0-dim tensor
- td_error_per_sample (:obj:`torch.Tensor`): nstep td error, 1-dim tensor
Shapes:
- data (:obj:`q_nstep_td_data`): the q_nstep_td_data containing\
['q', 'next_n_q', 'action', 'reward', 'done']
- q (:obj:`torch.FloatTensor`): :math:`(B, N)` i.e. [batch_size, action_dim]
- next_n_q (:obj:`torch.FloatTensor`): :math:`(B, N)`
- action (:obj:`torch.LongTensor`): :math:`(B, )`
- next_n_action (:obj:`torch.LongTensor`): :math:`(B, )`
- reward (:obj:`torch.FloatTensor`): :math:`(T, B)`, where T is timestep(nstep)
- done (:obj:`torch.BoolTensor`) :math:`(B, )`, whether done in last timestep
- td_error_per_sample (:obj:`torch.FloatTensor`): :math:`(B, )`
"""
q, next_n_q, action, next_n_action, reward, done, weight = data
assert len(action.shape) == 1, action.shape
if weight is None:
weight = torch.ones_like(action)
batch_range = torch.arange(action.shape[0])
q_s_a = q[batch_range, action]
target_v = alpha * torch.log(torch.sum(torch.exp(next_n_q / alpha), 1))
target_v[target_v == float("Inf")] = 20
target_v[target_v == float("-Inf")] = -20
# For an appropriate hyper-parameter alpha, these hardcodes can be removed.
# However, algorithms may face the danger of explosion for other alphas.
# The hardcodes above are to prevent this situation from happening
record_target_v = copy.deepcopy(target_v) #add the value function into tensorboard
if cum_reward:
if value_gamma is None:
target_v = reward + (gamma ** nstep) * target_v * (1 - done)
else:
target_v = reward + value_gamma * target_v * (1 - done)
else:
target_v = nstep_return(nstep_return_data(reward, target_v, done), gamma, nstep, value_gamma)
td_error_per_sample = criterion(q_s_a, target_v.detach())
return (td_error_per_sample * weight).mean(), td_error_per_sample, record_target_v
我们在实现SQIL/SQL策略时使用了epsilon-greedy策略。我们选择动作的方式在ding/model/wrappers/model_wrappers.py中的EpsGreedySampleWrapper_sql中实现。
class EpsGreedySampleWrapperSql(IModelWrapper):
def forward(self, *args, **kwargs):
eps = kwargs.pop('eps')
alpha = kwargs.pop('alpha')
output = self._model.forward(*args, **kwargs)
assert isinstance(output, dict), "model output must be dict, but find {}".format(type(output))
logit = output['logit']
assert isinstance(logit, torch.Tensor) or isinstance(logit, list)
if isinstance(logit, torch.Tensor):
logit = [logit]
if 'action_mask' in output:
mask = output['action_mask']
if isinstance(mask, torch.Tensor):
mask = [mask]
logit = [l.sub_(1e8 * (1 - m)) for l, m in zip(logit, mask)]
else:
mask = None
action = []
for i, l in enumerate(logit):
if np.random.random() > eps:
prob = torch.softmax(output['logit'] / alpha, dim=-1)
prob = prob / torch.sum(prob, 1, keepdims=True)
pi_action = torch.zeros(prob.shape)
pi_action = Categorical(prob)
pi_action = pi_action.sample()
action.append(pi_action)
else:
if mask:
action.append(sample_action(prob=mask[i].float()))
else:
action.append(torch.randint(0, l.shape[-1], size=l.shape[:-1]))
if len(action) == 1:
action, logit = action[0], logit[0]
output['action'] = action
return output
我们有两个缓冲区:一个缓冲区用于通过与环境的交互收集的新数据,另一个用于演示数据。我们在线获取演示数据。也就是说,在收集阶段,我们使用一个训练有素的模型生成数据,并将其推入演示缓冲区。在学习过程中,我们从这两个缓冲区中分别采样,如下所示:
# During the learning stage
for i in range(cfg.policy.learn.update_per_collect):
train_data_new = replay_buffer_new.sample(
(learner.policy.get_attribute('batch_size') // 2), learner.train_iter
)
train_data_demonstration = replay_buffer_demonstration.sample(
(learner.policy.get_attribute('batch_size') // 2), learner.train_iter
)
if train_data_new is None and train_data_demonstration is None:
train_data = None
else:
train_data = train_data_new + train_data_demonstration
if train_data is not None:
learner.train(train_data, collector.envstep)
我们还需要修改新数据和演示数据的奖励。以CartPole环境为例:
new_data = collector.collect_data(learner.train_iter, policy_kwargs={'eps': eps})
for i in range(len(new_data)):
device = new_data[i]['obs'].device
new_data[i].reward = torch.tensor([0.]).to(device)
关于演示数据,我们可以保持这些奖励不变。对于一般的奖励修改,请参考ding//entry/serial_entry_sqil.py。
基准测试¶
环境 |
最佳平均奖励 |
评估结果 |
配置链接 |
比较 |
|---|---|---|---|---|
乒乓球 (PongNoFrameskip-v4) |
20 |
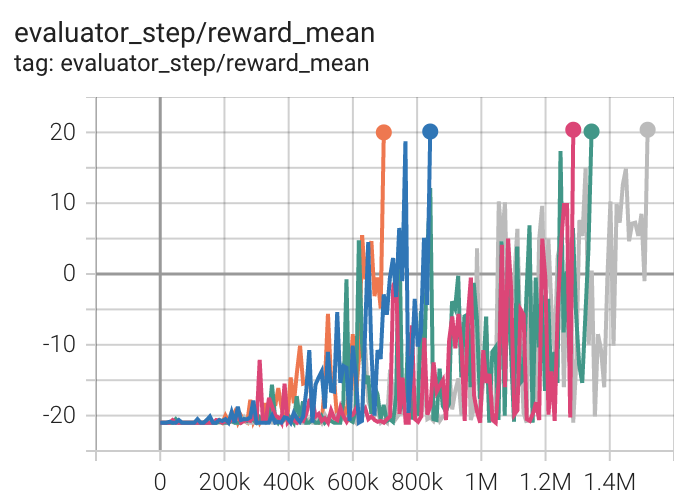
|
||
Qbert (QbertNoFrameskip-v4) |
14941 |
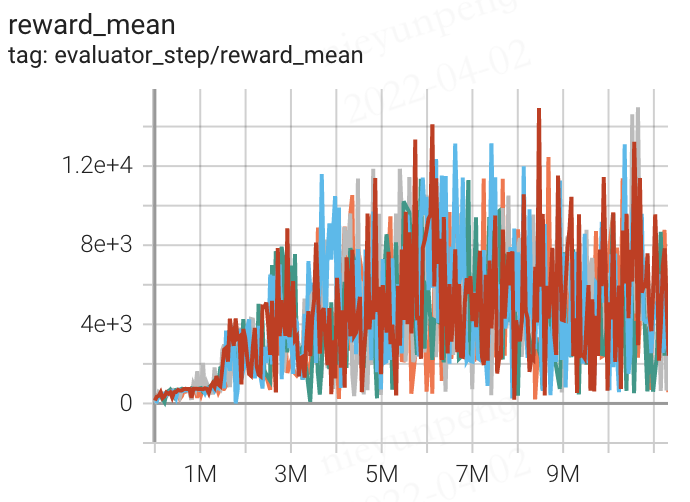
|
||
太空侵略者 (SpaceInvadersNoFrame skip-v4) |
1002 |
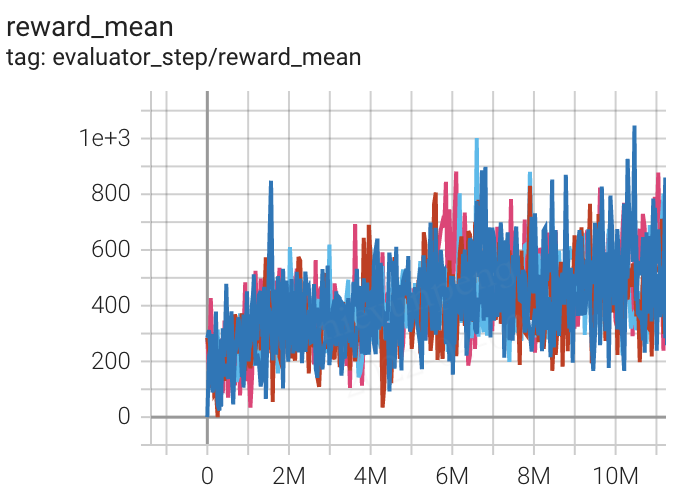
|
附注:
上述结果是通过在五个不同的随机种子(0, 1, 2, 3, 4)上运行相同的配置获得的
参考文献¶
Siddharth Reddy, Anca D. Dragan, Sergey Levine: “SQIL: 通过稀疏奖励的强化学习进行模仿学习”, 2019; [https://arxiv.org/abs/1905.11108 arXiv:1905.11108].
Haarnoja, Tuomas, 等. “基于深度能量的强化学习策略.” 国际机器学习会议. PMLR, 2017.
Piot, Bilal, Matthieu Geist, 和 Olivier Pietquin. “用于学徒学习的增强和奖励正则化分类。” 2014年国际自主代理和多代理系统会议论文集。2014年。