VPN¶

概述¶

值预测网络（VPN）首次在2017年NeurIPS的值预测网络中提出。值预测网络是对传统基于模型的强化学习算法的改进，也是Muzero算法的前身。

VPN算法的主要动机是，RL的规划阶段只需要预测未来的奖励和价值，而不需要预测未来的观察结果。

VPN 通过 Q-learning 学习预测值，同时通过监督学习学习奖励， VPN 执行前瞻规划以选择动作并计算引导目标 Q 值。

（即，学习一个抽象状态空间的动态，足以计算未来的奖励和价值）

快速事实¶

VPN 可以被视为基于模型的强化学习和无模型强化学习的结合。
VPN的基于模型的部分是学习一个足以计算未来奖励和价值的抽象状态空间的动态，而VPN的无模型部分是将学习到的抽象状态映射到奖励和价值。
VPN 结合了时间差分搜索和 n 步 Q 学习来进行训练。
VPN与其他基于模型的算法相比，主要性能改进在于VPN对环境中的随机性比观察预测模型方法更具鲁棒性。
为了解决基于模型算法存在的一些问题，VPN提出了一种介于传统基于模型算法和无模型算法之间的方法，使用动态模型对环境进行建模。
从基于模型的角度来看，动态模型通过提取抽象状态的形式来建模环境的状态转换过程、奖励和折扣函数。
从无模型的角度来看，通过动态模型提取抽象状态可以被视为训练评论者预测奖励和价值的辅助任务，以便更好地提取状态的相关表示。
VPN使用简单的推出和光束搜索，VPN + 蒙特卡洛树搜索(MCTS) \(\approxeq\) Muzero。

注意

基于模型的算法具有更好的样本效率，但更为复杂；无模型算法的样本效率较低，但相对简单且易于实现。由于复杂性，基于模型的算法不如无模型算法流行，并且主要用于数据获取成本较高的环境，例如机械臂控制。这是因为基于模型的算法涉及环境建模，导致建模过程复杂。此外，环境建模还需要训练，基于模型的方法的整体训练过程比无模型方法困难得多。大多数由基于模型算法建模的环境模型使用观察和动作来预测下一个观察和奖励。这种模型被称为观察预测模型。在相对复杂的环境中，观察通常具有更高的维度并且具有高度的随机性，这使得基于模型的算法难以学习与环境对应的观察预测模型。

关键方程或关键图表¶

价值预测网络主要由4部分组成：

VPN由以下模块组成，这些模块由\(\theta=\left\{\theta^{\text {enc }}, \theta^{\text {value }}, \theta^{\text {out }}, \theta^{\text {trans }}\right\}\)参数化：

编码 \(f_{\theta}^{\text {enc }}: \mathbf{x} \mapsto \mathbf{s} \quad\)

值 \(f_{\theta}^{\text {value }}: \mathbf{s} \mapsto V_{\theta}(\mathbf{s})\)

结果 \(f_{\theta}^{\text {out }}: \mathbf{s}, \mathbf{o} \mapsto r, \gamma\)

过渡 \(f_{\theta}^{\text {trans }}:\) s, \(\mathbf{o} \mapsto \mathbf{s}^{\prime}\)

编码模块使用神经网络（例如，用于视觉观察的CNN）将观察\((\mathbf{x})\)映射到抽象状态\(\left(\mathbf{s} \in \mathbb{R}^{m}\right)\)。因此，\(\mathbf{s}\)是一个将由网络学习的抽象状态表示（而不是环境状态或甚至其近似值）。
价值模块估计抽象状态\(\left(V_{\theta}(\mathbf{s})\right)\)的值。请注意，价值模块不是观察的函数，而是抽象状态的函数。
结果模块预测在抽象状态 s 执行选项 \(\mathbf{0}\) 的选项奖励 \((r \in \mathbb{R})\)。如果选项在终止前执行了 \(k\) 个原始动作，结果模块应预测这 \(k\) 个即时奖励的折现总和为一个标量。结果模块还预测由选项执行的步骤数引起的选项折现 \((\gamma \in \mathbb{R})\)。
过渡模块以选项条件的方式将抽象状态转换为下一个抽象状态 \(\left(\mathbf{s}^{\prime} \in \mathbb{R}^{m}\right)\)。

Q值可以通过以上四个部分进行估计，即输入观察值和相应的选项（动作），并输出相应的值估计。

对应的Q值预测公式为：

\(Q_{\theta}^{d}(\mathbf{s}, \mathbf{o})=r+\gamma V_{\theta}^{d}\left(\mathbf{s}^{\prime}\right) \quad V_{\theta}^{d}(\mathbf{s})=\left\{\begin{array}{ll} V_{\theta}(\mathbf{s}) & \text { 如果 } d=1 \\ \frac{1}{d} V_{\theta}(\mathbf{s})+\frac{d-1}{d} \max _{\mathbf{0}} Q_{\theta}^{d-1}(\mathbf{s}, \mathbf{o}) & \text { 如果 } d>1 \end{array}\right.\)

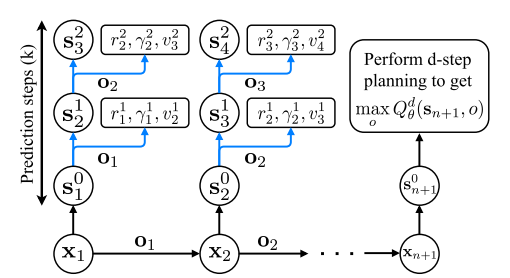
d步规划过程如下所示：

在训练时，VPN 使用 k 步预测进行训练：

\(\mathbf{s}_{t}^{k}=\left\{\begin{array}{ll} f_{\theta}^{\text {enc }}\left(\mathbf{x}_{t}\right) & \text { 如果 } k=0 \\ f_{\theta}^{\text {trans }}\left(\mathbf{s}_{t-1}^{k-1}, \mathbf{o}_{t-1}\right) & \text { 如果 } k>0 \end{array} \quad v_{t}^{k}=f_{\theta}^{\text {value }}\left(\mathbf{s}_{t}^{k}\right) \quad r_{t}^{k}, \gamma_{t}^{k}=f_{\theta}^{\text {out }}\left(\mathbf{s}_{t}^{k-1}, \mathbf{o}_{t}\right)\right.\)

整个更新流程图如下：

伪代码¶

扩展¶

VPN 可以与以下内容结合使用：
- 蒙特卡洛树搜索(MCTS)
  
  在VPN论文中，作者提到VPN算法与其他树搜索算法（如MCTS）兼容，但在具体实验中，论文为了简化使用了简单的Rollout。 Mastering Atari, Go, Chess and Shogi by Planning with a Learned Model 用MCTS替换了简单的Rollout，并在一系列具有挑战性和视觉复杂性的领域中实现了超人类的表现，而无需了解其底层动态。

实现¶

默认配置定义如下：

待定

使用的网络接口VPN定义如下：

待定

参考¶

Junhyuk Oh, Satinder Singh, Honglak Lee: “价值预测网络”, 2017; [http://arxiv.org/abs/1707.03497 arXiv:1707.03497].

朱利安·施里特维泽、约安尼斯·安东诺格鲁、托马斯·休伯特、卡伦·西蒙扬、洛朗·西弗雷、西蒙·施密特、亚瑟·格兹、爱德华·洛克哈特、德米斯·哈萨比斯、托尔·格雷佩尔、蒂莫西·利利克拉普、大卫·西尔弗：“通过使用学习模型进行规划掌握Atari、围棋、国际象棋和将棋”，2019年；[http://arxiv.org/abs/1911.08265 arXiv:1911.08265]。DOI：[https://dx.doi.org/10.1038/s41586-020-03051-4 10.1038/s41586-020-03051-4]。