在线商店中的因果归因和根本原因分析

本笔记本是对应博客文章的扩展和更新版本：使用DoWhy进行根因分析，一个用于因果机器学习的开源Python库

在这个例子中，我们查看一个在线商店并分析不同因素如何影响我们的利润。特别是，我们想要分析利润意外下降的原因并确定其潜在的根本原因。为此，我们可以利用图形因果模型（GCM）。

场景

假设我们在一个在线商店销售一款零售价为999美元的智能手机。产品的总利润取决于多个因素，例如销售数量、运营成本或广告支出。另一方面，例如销售数量取决于产品页面的访问量、价格本身以及潜在的促销活动。假设我们观察到2021年产品的利润稳定，但在2022年初突然出现了显著的利润下降。为什么？

在以下场景中，我们将使用DoWhy来更好地理解影响利润的因素的因果影响，并识别利润下降的原因。为了分析我们当前的问题，我们首先需要定义我们对因果关系的信念。为此，我们收集了影响利润的不同因素的每日记录。这些因素包括：

• 购物活动？: 一个二进制值，表示是否发生了特殊的购物活动，例如黑色星期五或网络星期一的销售。

• 广告支出: 广告活动的支出。

• 页面浏览量: 产品详情页的访问次数。

• 单价: 设备的价格，可能会因临时折扣而有所不同。

• 销售单位: 售出的手机数量。

• 收入: 每日收入。

• 运营成本: 包括生产成本、广告支出、行政费用等的日常运营费用。

• 利润: 每日利润。

查看这些属性，我们可以利用我们的领域知识以有向无环图的形式描述因果关系，这代表了我们在下面的因果图。图如下所示：

from IPython.display import Image
Image('online-shop-graph.png')

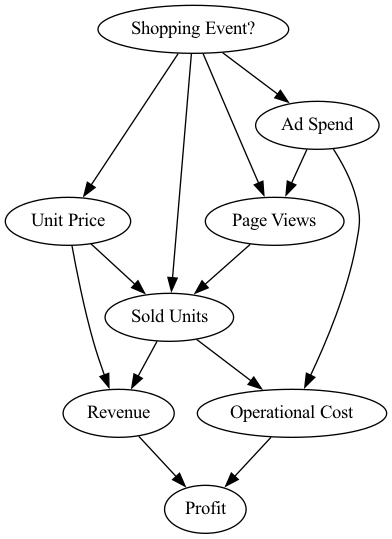
在这种情况下，我们知道以下内容：

Shopping Event? impacts:

→ Ad Spend: To promote the product on special shopping events, we require additional ad spending.

→ Page Views: Shopping events typically attract a large number of visitors to an online retailer due to discounts and various offers.

→ Unit Price: Typically, retailers offer some discount on the usual retail price on days with a shopping event.

→ Sold Units: Shopping events often take place during annual celebrations like Christmas, Father’s day, etc, when people often buy more than usual.

Ad Spend impacts:

→ Page Views: The more we spend on ads, the more likely people will visit the product page.

→ Operational Cost: Ad spending is part of the operational cost.

Page Views impacts:

→ Sold Units: The more people visiting the product page, the more likely the product is bought. This is quite obvious seeing that if no one would visit the page, there wouldn’t be any sale.

Unit Price impacts:

→ Sold Units: The higher/lower the price, the less/more units are sold.

→ Revenue: The daily revenue typically consist of the product of the number of sold units and unit price.

Sold Units impacts:

→ Sold Units: Same argument as before, the number of sold units heavily influences the revenue.

→ Operational Cost: There is a manufacturing cost for each unit we produce and sell. The more units we well the higher the revenue, but also the higher the manufacturing costs.

Operational Cost impacts:

→ Profit: The profit is based on the generated revenue minus the operational cost.

Revenue impacts:

→ Profit: Same reason as for the operational cost.

步骤1：定义因果模型

现在，让我们为这些因果关系建模。第一步，我们需要定义一个所谓的结构因果模型（SCM），它是因果图和描述数据生成过程的底层生成模型的组合。

因果图可以通过以下方式定义：

import networkx as nx

causal_graph = nx.DiGraph([('Page Views', 'Sold Units'),
                           ('Revenue', 'Profit'),
                           ('Unit Price', 'Sold Units'),
                           ('Unit Price', 'Revenue'),
                           ('Shopping Event?', 'Page Views'),
                           ('Shopping Event?', 'Sold Units'),
                           ('Shopping Event?', 'Unit Price'),
                           ('Shopping Event?', 'Ad Spend'),
                           ('Ad Spend', 'Page Views'),
                           ('Ad Spend', 'Operational Cost'),
                           ('Sold Units', 'Revenue'),
                           ('Sold Units', 'Operational Cost'),
                           ('Operational Cost', 'Profit')])

为了验证我们没有遗漏任何边，我们可以绘制这个图：

from dowhy.utils import plot

plot(causal_graph)

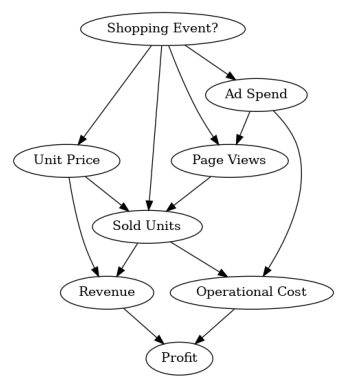
接下来，我们查看2021年的数据：

import pandas as pd
import numpy as np

pd.options.display.float_format = '${:,.2f}'.format  # Format dollar columns

data_2021 = pd.read_csv('2021 Data.csv', index_col='Date')
data_2021.head()

	购物活动？	广告支出	页面浏览量	单价	销售单位	收入	运营成本	利润
日期
2021-01-01	假	$1,490.49	11861	$999.00	2317	$2,314,683.00	$1,659,999.89	$654,683.11
2021-01-02	假	$1,455.92	11776	$999.00	2355	$2,352,645.00	$1,678,959.08	$673,685.92
2021-01-03	False	$1,405.82	11861	$999.00	2391	$2,388,609.00	$1,696,906.14	$691,702.86
2021-01-04	假	$1,379.30	11677	$999.00	2344	$2,341,656.00	$1,673,380.64	$668,275.36
2021-01-05	假	$1,234.20	11871	$999.00	2412	$2,409,588.00	$1,707,252.61	$702,335.39

正如我们所看到的，我们拥有2021年每天的一个样本，其中包含因果图中的所有变量。请注意，在我们这里考虑的合成数据中，购物事件也是随机生成的。

我们定义了因果图，但我们仍然需要为节点分配生成模型。我们可以手动指定这些模型，并在需要时进行配置，或者使用数据中的启发式方法自动推断“合适”的模型。我们将在这里利用后者：

from dowhy import gcm
gcm.util.general.set_random_seed(0)

# Create the structural causal model object
scm = gcm.StructuralCausalModel(causal_graph)

# Automatically assign generative models to each node based on the given data
auto_assignment_summary = gcm.auto.assign_causal_mechanisms(scm, data_2021)

只要有可能，我们建议根据先验知识分配模型，因为这样模型可以紧密地模仿领域的物理特性，而不依赖于数据的细微差别。然而，在这里我们让DoWhy为我们完成这项工作。

在自动分配模型后，我们可以打印摘要以获取有关所选模型的一些见解：

print(auto_assignment_summary)

When using this auto assignment function, the given data is used to automatically assign a causal mechanism to each node. Note that causal mechanisms can also be customized and assigned manually.
The following types of causal mechanisms are considered for the automatic selection:

If root node:
An empirical distribution, i.e., the distribution is represented by randomly sampling from the provided data. This provides a flexible and non-parametric way to model the marginal distribution and is valid for all types of data modalities.

If non-root node and the data is continuous:
Additive Noise Models (ANM) of the form X_i = f(PA_i) + N_i, where PA_i are the parents of X_i and the unobserved noise N_i is assumed to be independent of PA_i.To select the best model for f, different regression models are evaluated and the model with the smallest mean squared error is selected.Note that minimizing the mean squared error here is equivalent to selecting the best choice of an ANM.

If non-root node and the data is discrete:
Discrete Additive Noise Models have almost the same definition as non-discrete ANMs, but come with an additional constraint for f to only return discrete values.
Note that 'discrete' here refers to numerical values with an order. If the data is categorical, consider representing them as strings to ensure proper model selection.

If non-root node and the data is categorical:
A functional causal model based on a classifier, i.e., X_i = f(PA_i, N_i).
Here, N_i follows a uniform distribution on [0, 1] and is used to randomly sample a class (category) using the conditional probability distribution produced by a classification model.Here, different model classes are evaluated using the (negative) F1 score and the best performing model class is selected.

In total, 8 nodes were analyzed:

--- Node: Shopping Event?
Node Shopping Event? is a root node. Therefore, assigning 'Empirical Distribution' to the node representing the marginal distribution.

--- Node: Unit Price
Node Unit Price is a non-root node with continuous data. Assigning 'AdditiveNoiseModel using LinearRegression' to the node.
This represents the causal relationship as Unit Price := f(Shopping Event?) + N.
For the model selection, the following models were evaluated on the mean squared error (MSE) metric:
LinearRegression: 142.77431246551515
Pipeline(steps=[('polynomialfeatures', PolynomialFeatures(include_bias=False)),
                ('linearregression', LinearRegression)]): 142.78271703597315
HistGradientBoostingRegressor: 439.63843778273156

--- Node: Ad Spend
Node Ad Spend is a non-root node with continuous data. Assigning 'AdditiveNoiseModel using LinearRegression' to the node.
This represents the causal relationship as Ad Spend := f(Shopping Event?) + N.
For the model selection, the following models were evaluated on the mean squared error (MSE) metric:
LinearRegression: 15950.378625434218
Pipeline(steps=[('polynomialfeatures', PolynomialFeatures(include_bias=False)),
                ('linearregression', LinearRegression)]): 16057.728423653647
HistGradientBoostingRegressor: 80313.4296584338

--- Node: Page Views
Node Page Views is a non-root node with discrete data. Assigning 'Discrete AdditiveNoiseModel using Pipeline' to the node.
This represents the discrete causal relationship as Page Views := f(Ad Spend,Shopping Event?) + N.
For the model selection, the following models were evaluated on the mean squared error (MSE) metric:
Pipeline(steps=[('polynomialfeatures', PolynomialFeatures(include_bias=False)),
                ('linearregression', LinearRegression)]): 83938.3537814653
LinearRegression: 85830.1184468119
HistGradientBoostingRegressor: 1428896.628193814

--- Node: Sold Units
Node Sold Units is a non-root node with discrete data. Assigning 'Discrete AdditiveNoiseModel using LinearRegression' to the node.
This represents the discrete causal relationship as Sold Units := f(Page Views,Shopping Event?,Unit Price) + N.
For the model selection, the following models were evaluated on the mean squared error (MSE) metric:
LinearRegression: 8904.890796950855
Pipeline(steps=[('polynomialfeatures', PolynomialFeatures(include_bias=False)),
                ('linearregression', LinearRegression)]): 14157.831817904153
HistGradientBoostingRegressor: 231668.29855446037

--- Node: Revenue
Node Revenue is a non-root node with continuous data. Assigning 'AdditiveNoiseModel using Pipeline' to the node.
This represents the causal relationship as Revenue := f(Sold Units,Unit Price) + N.
For the model selection, the following models were evaluated on the mean squared error (MSE) metric:
Pipeline(steps=[('polynomialfeatures', PolynomialFeatures(include_bias=False)),
                ('linearregression', LinearRegression)]): 1.0800435888102176e-18
LinearRegression: 69548987.23197266
HistGradientBoostingRegressor: 155521789447.02286

--- Node: Operational Cost
Node Operational Cost is a non-root node with continuous data. Assigning 'AdditiveNoiseModel using LinearRegression' to the node.
This represents the causal relationship as Operational Cost := f(Ad Spend,Sold Units) + N.
For the model selection, the following models were evaluated on the mean squared error (MSE) metric:
LinearRegression: 38.71409364534825
Pipeline(steps=[('polynomialfeatures', PolynomialFeatures(include_bias=False)),
                ('linearregression', LinearRegression)]): 39.01584891167706
HistGradientBoostingRegressor: 18332123695.022976

--- Node: Profit
Node Profit is a non-root node with continuous data. Assigning 'AdditiveNoiseModel using LinearRegression' to the node.
This represents the causal relationship as Profit := f(Operational Cost,Revenue) + N.
For the model selection, the following models were evaluated on the mean squared error (MSE) metric:
LinearRegression: 1.852351985649207e-18
Pipeline(steps=[('polynomialfeatures', PolynomialFeatures(include_bias=False)),
                ('linearregression', LinearRegression)]): 2.8418485593830953e-06
HistGradientBoostingRegressor: 22492460598.32865

===Note===
Note, based on the selected auto assignment quality, the set of evaluated models changes.
For more insights toward the quality of the fitted graphical causal model, consider using the evaluate_causal_model function after fitting the causal mechanisms.

正如我们所看到的，虽然自动分配也考虑了非线性模型，但对于大多数关系来说，线性模型已经足够，除了收入，它是销售单位和单位价格的乘积。

步骤2：将因果模型拟合到数据

在为每个节点分配模型后，我们需要学习模型的参数：

gcm.fit(scm, data_2021)

Fitting causal mechanism of node Operational Cost: 100%|██████████| 8/8 [00:00<00:00, 365.79it/s]

fit 方法学习每个节点中生成模型的参数。在我们继续之前，让我们快速看一下因果机制的性能以及它们如何捕捉分布：

print(gcm.evaluate_causal_model(scm, data_2021, compare_mechanism_baselines=True, evaluate_invertibility_assumptions=False, evaluate_causal_structure=False))

Evaluating causal mechanisms...: 100%|██████████| 8/8 [00:00<00:00, 882.76it/s]

Evaluated the performance of the causal mechanisms and the overall average KL divergence between generated and observed distribution. The results are as follows:

==== Evaluation of Causal Mechanisms ====
The used evaluation metrics are:
- KL divergence (only for root-nodes): Evaluates the divergence between the generated and the observed distribution.
- Mean Squared Error (MSE): Evaluates the average squared differences between the observed values and the conditional expectation of the causal mechanisms.
- Normalized MSE (NMSE): The MSE normalized by the standard deviation for better comparison.
- R2 coefficient: Indicates how much variance is explained by the conditional expectations of the mechanisms. Note, however, that this can be misleading for nonlinear relationships.
- F1 score (only for categorical non-root nodes): The harmonic mean of the precision and recall indicating the goodness of the underlying classifier model.
- (normalized) Continuous Ranked Probability Score (CRPS): The CRPS generalizes the Mean Absolute Percentage Error to probabilistic predictions. This gives insights into the accuracy and calibration of the causal mechanisms.
NOTE: Every metric focuses on different aspects and they might not consistently indicate a good or bad performance.
We will mostly utilize the CRPS for comparing and interpreting the performance of the mechanisms, since this captures the most important properties for the causal model.

--- Node Shopping Event?
- The KL divergence between generated and observed distribution is 0.019221919686426836.
The estimated KL divergence indicates an overall very good representation of the data distribution.

--- Node Unit Price
- The MSE is 156.48090806251736.
- The NMSE is 0.6938977880013996.
- The R2 coefficient is 0.35194776992616694.
- The normalized CRPS is 0.12553014444452665.
The estimated CRPS indicates a very good model performance.
The mechanism is better or equally good than all 7 baseline mechanisms.

--- Node Ad Spend
- The MSE is 16677.202023167338.
- The NMSE is 0.48344956888514795.
- The R2 coefficient is 0.7512082042758019.
- The normalized CRPS is 0.2720127266162416.
The estimated CRPS indicates a good model performance.
The mechanism is better or equally good than all 7 baseline mechanisms.

--- Node Page Views
- The MSE is 77900.05479452056.
- The NMSE is 0.3462130891886136.
- The R2 coefficient is 0.7335844848896803.
- The normalized CRPS is 0.1803592381314227.
The estimated CRPS indicates a very good model performance.
The mechanism is better or equally good than all 7 baseline mechanisms.

--- Node Sold Units
- The MSE is 8758.161643835618.
- The NMSE is 0.1340557695877285.
- The R2 coefficient is 0.981600440084566.
- The normalized CRPS is 0.056745468190872575.
The estimated CRPS indicates a very good model performance.
The mechanism is better or equally good than all 7 baseline mechanisms.

--- Node Revenue
- The MSE is 1.7763093127296757e-19.
- The NMSE is 6.786229331465976e-16.
- The R2 coefficient is 1.0.
- The normalized CRPS is 1.4574679362932044e-16.
The estimated CRPS indicates a very good model performance.
The mechanism is better or equally good than all 7 baseline mechanisms.

--- Node Operational Cost
- The MSE is 38.48242630536858.
- The NMSE is 1.820517232232272e-05.
- The R2 coefficient is 0.9999999996455899.
- The normalized CRPS is 1.001979239428077e-05.
The estimated CRPS indicates a very good model performance.
The mechanism is better or equally good than all 7 baseline mechanisms.

--- Node Profit
- The MSE is 1.5832322135199285e-18.
- The NMSE is 4.723810955181931e-15.
- The R2 coefficient is 1.0.
- The normalized CRPS is 3.157782102773924e-16.
The estimated CRPS indicates a very good model performance.
The mechanism is better or equally good than all 7 baseline mechanisms.

==== Evaluation of Generated Distribution ====
The overall average KL divergence between the generated and observed distribution is 1.0102049246719438
The estimated KL divergence indicates some mismatches between the distributions.

==== NOTE ====
Always double check the made model assumptions with respect to the graph structure and choice of causal mechanisms.
All these evaluations give some insight into the goodness of the causal model, but should not be overinterpreted, since some causal relationships can be intrinsically hard to model. Furthermore, many algorithms are fairly robust against misspecifications or poor performances of causal mechanisms.

拟合的因果机制相当好地代表了数据生成过程，尽管存在一些小的不准确性。然而，考虑到样本量较小以及许多节点的信噪比较低，这是可以预期的。最重要的是，所有基线机制的表现都没有更好，这表明我们的模型选择是合适的。基于评估，我们也不拒绝给定的因果图。

基线模型的选择也可以进行配置。更多详情，请查看相应的evaluate_causal_model文档。

步骤3：回答因果问题

生成新样本

既然我们已经了解了数据生成过程，我们也可以生成新的样本：

gcm.draw_samples(scm, num_samples=10)

	购物活动？	单价	广告支出	页面浏览量	销售单位	收入	运营成本	利润
0	假	$999.00	$1,226.62	11761	2355	$2,352,645.00	$1,678,734.40	$673,910.60
1	假	$999.00	$1,452.27	11680	2309	$2,306,691.00	$1,655,963.89	$650,727.11
2	假	$999.00	$1,258.09	11849	2357	$2,354,643.00	$1,679,769.27	$674,873.73
3	假	$999.00	$1,392.70	11637	2335	$2,332,665.00	$1,668,898.80	$663,766.20
4	假	$999.00	$1,217.63	11713	2311	$2,308,689.00	$1,656,722.94	$651,966.06
5	假	$999.00	$1,100.55	11720	2333	$2,330,667.00	$1,667,603.33	$663,063.67
6	假	$989.76	$1,240.77	11710	2394	$2,369,495.96	$1,698,243.13	$671,252.83
7	假	$999.00	$1,173.21	11444	2709	$2,706,291.00	$1,855,673.43	$850,617.57
8	假	$999.00	$1,326.60	11658	2350	$2,347,650.00	$1,676,334.74	$671,315.26
9	假	$999.00	$1,409.23	11845	2372	$2,369,628.00	$1,687,412.42	$682,215.58

我们从学习到的因果关系中抽取了10个样本。

影响利润差异的关键因素是什么？

此时，我们想要了解哪些因素推动了利润的变化。让我们首先更仔细地看一下利润随时间的变化。为此，我们绘制了2021年利润随时间的变化图，其中生成的图表在Y轴上显示利润（以美元为单位），在X轴上显示时间。

data_2021['Profit'].plot(ylabel='Profit in $', figsize=(15,5), rot=45)

<Axes: xlabel='Date', ylabel='Profit in $'>

我们看到全年利润有一些显著的波动。我们可以通过查看标准差来进一步量化这一点：

data_2021['Profit'].std()

$\displaystyle 259247.66010978$

估计的标准偏差约为259247美元，这是相当显著的。查看因果图，我们可以看到收入和运营成本对利润有直接影响，但它们中哪一个对方差的贡献最大？为了找出这一点，我们可以利用直接箭头强度算法，该算法量化了图中特定箭头的因果影响：

import numpy as np

# Note: The percentage conversion only makes sense for purely positive attributions.
def convert_to_percentage(value_dictionary):
    total_absolute_sum = np.sum([abs(v) for v in value_dictionary.values()])
    return {k: abs(v) / total_absolute_sum * 100 for k, v in value_dictionary.items()}


arrow_strengths = gcm.arrow_strength(scm, target_node='Profit')

plot(causal_graph,
     causal_strengths=convert_to_percentage(arrow_strengths),
     figure_size=[15, 10])

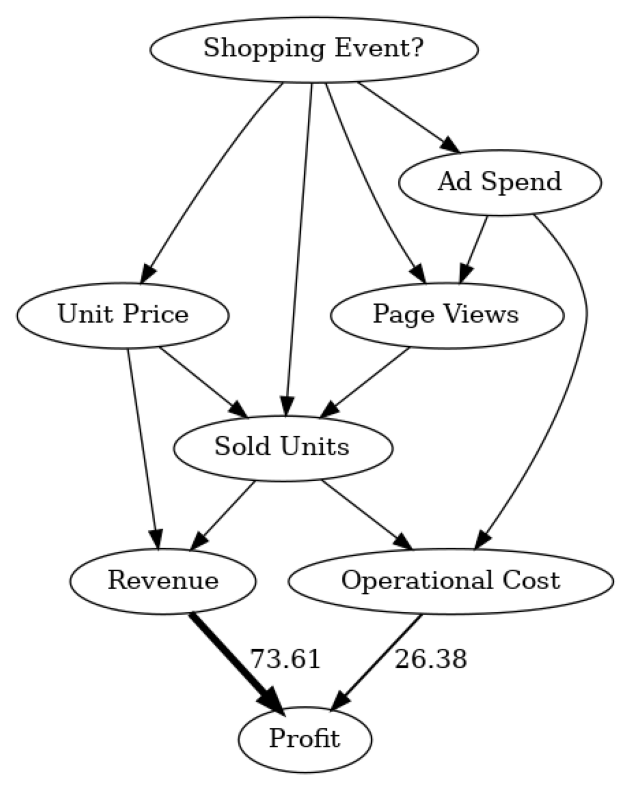
在这个因果图中，我们可以看到每个节点对利润方差的贡献有多大。为了简化，贡献被转换为百分比。由于利润本身只是收入和运营成本之间的差额，我们不期望有更多因素影响方差。正如我们所看到的，收入的影响比运营成本更大。这是有道理的，因为收入通常比运营成本变化更大，这是由于对销售单位数量的更强依赖性。请注意，直接箭头强度方法也支持使用其他类型的度量，例如KL散度。

虽然直接影响有助于理解哪些直接父节点对利润的方差影响最大，但这主要证实了我们之前的信念。然而，哪个因素最终应对这种高方差负责的问题仍然不清楚。例如，收入本身基于销售单位和单位价格。尽管我们可以递归地将直接箭头强度应用于所有节点，但我们无法正确加权地了解上游节点对方差的影响。

哪些重要的因果因素导致了利润的差异？为了找出这一点，我们可以使用内在因果贡献方法，该方法通过仅考虑节点新添加的信息，而不是从其父节点继承的信息，将利润的差异归因于因果图中的上游节点。例如，一个节点如果只是其父节点的重新缩放版本，则不会有任何内在贡献。更多详情请参见相应的研究论文。

让我们将方法应用于数据：

iccs = gcm.intrinsic_causal_influence(scm, target_node='Profit', num_samples_randomization=500)

Evaluating set functions...: 100%|██████████| 120/120 [02:37<00:00,  1.31s/it]

from dowhy.utils import bar_plot

bar_plot(convert_to_percentage(iccs), ylabel='Variance attribution in %')

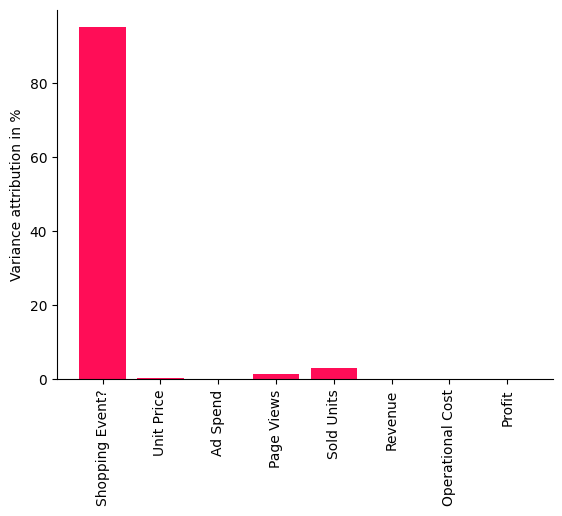
此条形图中显示的分数是百分比，表示每个节点对利润的方差贡献了多少——不继承因果图中其父节点的方差。正如我们清楚地看到的，购物事件对利润方差的影响最大。这是有道理的，因为在促销期间（如黑色星期五或Prime Day）销售受到很大影响，从而影响整体利润。令人惊讶的是，我们还发现诸如销售单位数量或页面浏览量等因素的影响相当小，即利润的大方差几乎可以完全由购物事件解释。让我们通过标记有购物事件的日子来直观地检查这一点。为此，我们再次使用pandas的绘图函数，但在图中用红色垂直线标记所有发生购物事件的点：

import matplotlib.pyplot as plt

data_2021['Profit'].plot(ylabel='Profit in $', figsize=(15,5), rot=45)
plt.vlines(np.arange(0, data_2021.shape[0])[data_2021['Shopping Event?']], data_2021['Profit'].min(), data_2021['Profit'].max(), linewidth=10, alpha=0.3, color='r')

<matplotlib.collections.LineCollection at 0x7ff10016d460>

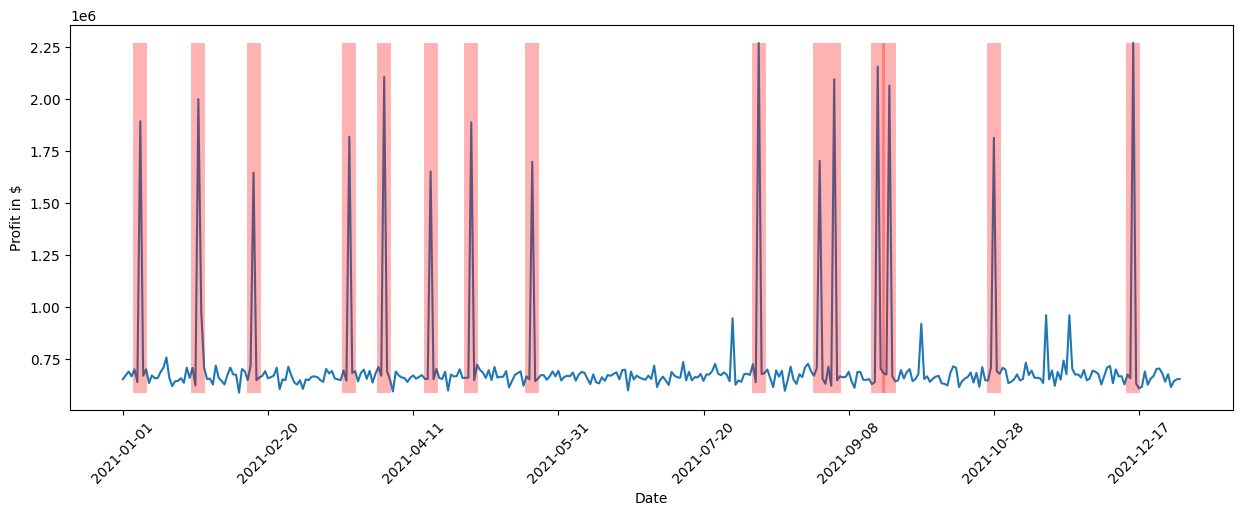
我们清楚地看到，购物事件与利润的高峰期相吻合。虽然我们可以通过查看各种不同的关系或使用领域知识来手动调查这一点，但随着系统复杂性的增加，任务变得更加困难。通过几行代码，我们从DoWhy中获得了这些见解。

解释某一天利润下降的关键因素是什么？

在利润方面取得成功的一年之后，新技术进入市场，因此我们希望保持利润并通过销售更多设备来减少过剩库存。为了增加需求，我们在2022年初将零售价格降低了10%。根据之前的分析，我们知道价格下降10%将大致增加需求13.75%，这是一个轻微的盈余。根据需求价格弹性模型，我们预计销售单位数量将增加约37.5%。让我们通过加载2022年第一天的数据并计算该天两年销售单位数量的比例来看看这是否属实：

first_day_2022 = pd.read_csv('2022 First Day.csv', index_col='Date')
(first_day_2022['Sold Units'][0] / data_2021['Sold Units'][0] - 1) * 100

$\displaystyle 18.9469141130773$

令人惊讶的是，我们只增加了约19%的销售单位数量。鉴于收入远低于预期，这肯定会影响利润。让我们与去年同期进行比较：

(1 - first_day_2022['Profit'][0] / data_2021['Profit'][0]) * 100

$\displaystyle 8.57891513840979$

事实上，利润下降了约8.5%。为什么会出现这种情况，尽管我们预期由于价格下降需求会大幅增加？让我们来调查一下这里发生了什么。

为了找出导致利润下降的原因，我们可以利用DoWhy的异常归因功能。在这里，我们只需要指定我们感兴趣的目标节点（利润）和我们想要分析的异常样本（2022年的第一天）。然后，这些结果会绘制在一个条形图中，显示每个节点在给定异常样本中的归因分数：

attributions = gcm.attribute_anomalies(scm, target_node='Profit', anomaly_samples=first_day_2022)

bar_plot({k: v[0] for k, v in attributions.items()}, ylabel='Anomaly attribution score')

Evaluating set functions...: 100%|██████████| 125/125 [00:03<00:00, 38.58it/s]

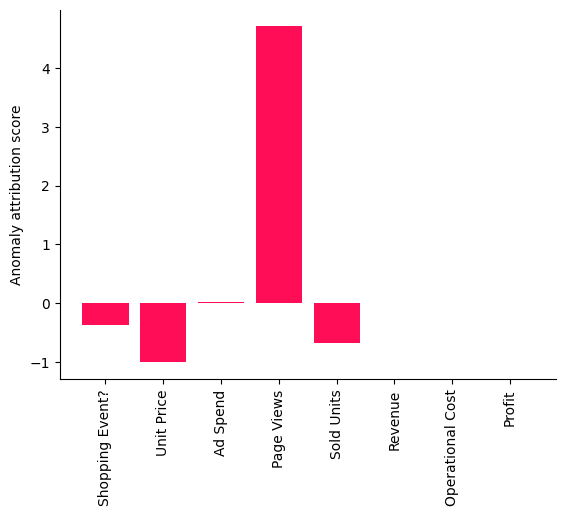
正归因分数意味着相应的节点对观察到的异常有贡献，在我们的案例中是利润的下降。节点的负分数表示该节点的观察值实际上减少了异常的可能性（例如，由于价格下降导致的需求增加应该会增加利润）。关于分数解释的更多细节可以在相应的研究论文中找到。有趣的是，页面浏览量作为解释当天利润下降的一个因素在所示的条形图中突出显示。

虽然这种方法为我们提供了特定模型和参数的点估计，我们还可以使用DoWhy的置信区间功能，该功能结合了拟合模型参数和算法近似的不确定性：

gcm.config.disable_progress_bars()  # We turn off the progress bars here to reduce the number of outputs.

median_attributions, confidence_intervals, = gcm.confidence_intervals(
    gcm.fit_and_compute(gcm.attribute_anomalies,
                        scm,
                        bootstrap_training_data=data_2021,
                        target_node='Profit',
                        anomaly_samples=first_day_2022),
    num_bootstrap_resamples=10)

bar_plot(median_attributions, confidence_intervals, 'Anomaly attribution score')

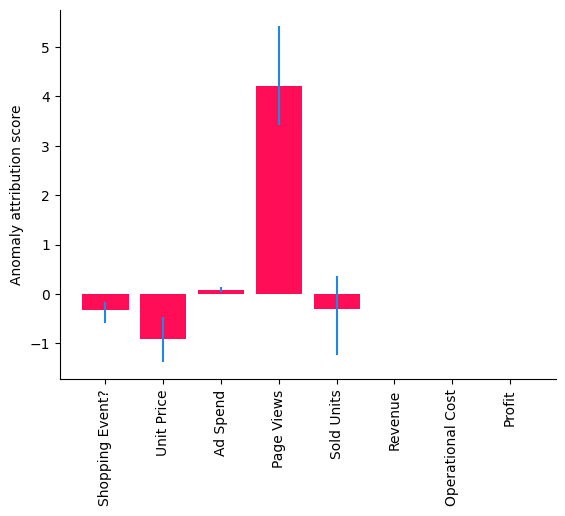
注意，在这个条形图中，我们看到在较小数据集上多次运行的中位数归因，每次运行都会重新拟合模型并重新评估归因。我们得到了与之前相似的图景，但“销售单位”归因的置信区间也包含零，这意味着其贡献不显著。但一些重要问题仍然存在：这是否只是巧合，如果不是，我们系统中的哪一部分发生了变化？为了找出答案，我们需要收集更多的数据。

请注意，结果会根据所选数据的不同而有所差异，因为它们是特定于样本的。在其他日期，其他因素可能相关。此外，请注意分析（包括置信区间）始终依赖于所做的建模假设。换句话说，如果模型发生变化或拟合不佳，也会预期得到不同的结果。

2022年第一季度利润下降的原因是什么？

虽然之前的分析基于单一观察，让我们看看这是否只是巧合，或者这是一个持续存在的问题。在准备季度业务报告时，我们有一些来自前三个月的数据。我们首先检查2022年第一季度的利润是否平均比2021年有所下降。与之前类似，我们可以通过计算2022年和2021年第一季度平均利润的比例来完成这一点：

data_first_quarter_2021 = data_2021[data_2021.index <= '2021-03-31']
data_first_quarter_2022 = pd.read_csv("2022 First Quarter.csv", index_col='Date')

(1 - data_first_quarter_2022['Profit'].mean() / data_first_quarter_2021['Profit'].mean()) * 100

$\displaystyle 13.0494881794224$

确实，2022年第一季度的利润下降是持续的。那么，这背后的根本原因是什么？让我们应用分布变化方法来识别系统中发生变化的部分：

median_attributions, confidence_intervals = gcm.confidence_intervals(
    lambda: gcm.distribution_change(scm,
                                    data_first_quarter_2021,
                                    data_first_quarter_2022,
                                    target_node='Profit',
                                    # Here, we are intersted in explaining the differences in the mean.
                                    difference_estimation_func=lambda x, y: np.mean(y) - np.mean(x))
)

bar_plot(median_attributions, confidence_intervals, 'Profit change attribution in $')

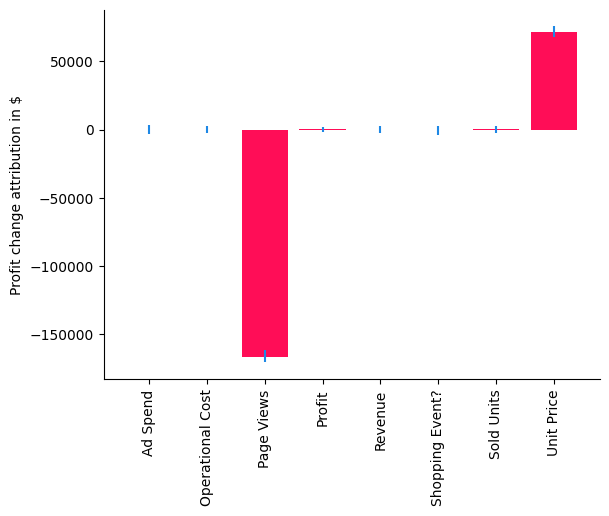
在我们的案例中，分布变化方法解释了利润平均值的变化，即负值表示节点对平均值有减少的贡献，正值表示有增加的贡献。通过使用条形图，我们现在可以清楚地看到，由于销售单位的增加，单价的变化实际上对预期利润有轻微的正面贡献，但问题似乎来自于页面浏览量，其值为负。虽然我们已经在2022年初理解这是下降的主要驱动因素，但我们现在已经隔离并确认页面浏览量也发生了变化。让我们与前一年的平均页面浏览量进行比较。

(1 - data_first_quarter_2022['Page Views'].mean() / data_first_quarter_2021['Page Views'].mean()) * 100

$\displaystyle 14.347627108364$

确实，页面浏览量下降了约14%。由于我们已经排除了所有其他潜在因素，现在我们可以更深入地研究页面浏览量，看看发生了什么。这是一个假设的情景，但我们可以想象，这可能是由于搜索算法的变化，导致该产品在搜索结果中的排名降低，从而减少了访问产品页面的客户数量。知道了这一点，我们现在可以开始缓解这个问题。

数据生成过程

虽然无法重现完全相同的数据，但以下数据集生成器应能提供非常相似类型的数据，并具有各种可调整的参数：

from dowhy.datasets import sales_dataset

data_2021 = sales_dataset(start_date="2021-01-01", end_date="2021-12-31")
data_2022 = sales_dataset(start_date="2022-01-01", end_date="2022-12-31", change_of_price=0.9)