注意
用于GeoPandas的PySAL分层分类方案#
 PySAL 是一个 `空间分析库 <>`__,它封装了用于各个领域的快速空间算法。这些领域包括探索性空间数据分析、空间不平等分析、网络上的空间分析、空间动态分析等。
PySAL 是一个 `空间分析库 <>`__,它封装了用于各个领域的快速空间算法。这些领域包括探索性空间数据分析、空间不平等分析、网络上的空间分析、空间动态分析等。
在使用一组颜色绘制度量时,它在Geopandas中被内部使用。根据不同的分类方案,有许多方法可以将数据分类到不同的区间中。
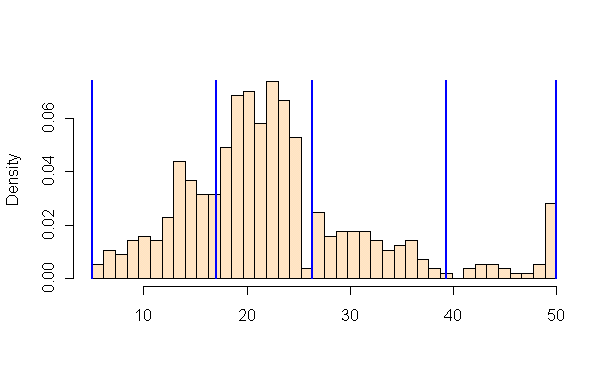
例如,如果我们有20个国家,其平均年温度在5C到25C之间,我们可以通过以下方式将它们分类为4个区间:
分位数
将行分成相等的部分,每个箱子5个国家。
等间隔
将度量的区间分成相等的部分,每个区间5C。
自然断点(Fischer Jenks)
该算法尝试将行分割成自然发生的簇。每个箱中的数量将取决于观察值在区间上的位置。
[1]:
import geopandas as gpd
import matplotlib.pyplot as plt
[2]:
# We use a PySAL example shapefile
import libpysal as ps
pth = ps.examples.get_path("columbus.shp")
tracts = gpd.GeoDataFrame.from_file(pth)
print("Observations, Attributes:", tracts.shape)
tracts.head()
Observations, Attributes: (49, 21)
[2]:
| 面积 | 周长 | COLUMBUS_ | COLUMBUS_I | POLYID | 邻接 | HOVAL | INC | 犯罪 | 开放 | ... | DISCBD | X | Y | NSA | NSB | 东西 | CP | 千 | 邻接编号 | 几何 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.309441 | 2.440629 | 2 | 5 | 1 | 5 | 80.467003 | 19.531 | 15.725980 | 2.850747 | ... | 5.03 | 38.799999 | 44.070000 | 1.0 | 1.0 | 1.0 | 0.0 | 1000.0 | 1005.0 | 多边形 ((8.62413 14.23698, 8.55970 14.74245, ... |
| 1 | 0.259329 | 2.236939 | 3 | 1 | 2 | 1 | 44.567001 | 21.232 | 18.801754 | 5.296720 | ... | 4.27 | 35.619999 | 42.380001 | 1.0 | 1.0 | 0.0 | 0.0 | 1000.0 | 1001.0 | 多边形 ((8.25279 14.23694, 8.28276 14.22994, ... |
| 2 | 0.192468 | 2.187547 | 4 | 6 | 3 | 6 | 26.350000 | 15.956 | 30.626781 | 4.534649 | ... | 3.89 | 39.820000 | 41.180000 | 1.0 | 1.0 | 1.0 | 0.0 | 1000.0 | 1006.0 | 多边形 ((8.65331 14.00809, 8.81814 14.00205, ... |
| 3 | 0.083841 | 1.427635 | 5 | 2 | 4 | 2 | 33.200001 | 4.477 | 32.387760 | 0.394427 | ... | 3.70 | 36.500000 | 40.520000 | 1.0 | 1.0 | 0.0 | 0.0 | 1000.0 | 1002.0 | 多边形 ((8.45950 13.82035, 8.47341 13.83227, ... |
| 4 | 0.488888 | 2.997133 | 6 | 7 | 5 | 7 | 23.225000 | 11.252 | 50.731510 | 0.405664 | ... | 2.83 | 40.009998 | 38.000000 | 1.0 | 1.0 | 1.0 | 0.0 | 1000.0 | 1007.0 | 多边形 ((8.68527 13.63952, 8.67758 13.72221, ... |
5 行 × 21 列
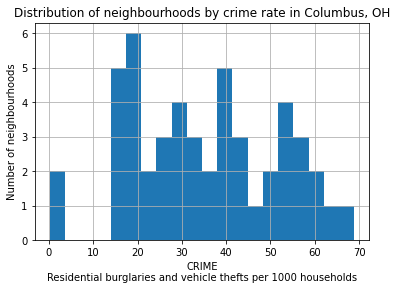
绘制犯罪变量#
在这个例子中,我们查看了俄亥俄州哥伦布市的邻里级别统计数据。我们想了解犯罪率变量在城市中的分布情况。
来自shapefile的元数据: >犯罪: 每千户家庭的住宅盗窃和车辆盗窃
[3]:
# Let's take a look at how the CRIME variable is distributed with a histogram
tracts["CRIME"].hist(bins=20)
plt.xlabel("CRIME\nResidential burglaries and vehicle thefts per 1000 households")
plt.ylabel("Number of neighbourhoods")
plt.title("Distribution of neighbourhoods by crime rate in Columbus, OH")
plt.show()
现在让我们看看没有分类方案的情况:
[4]:
tracts.plot(column="CRIME", cmap="OrRd", edgecolor="k", legend=True)
[4]:
<AxesSubplot:>
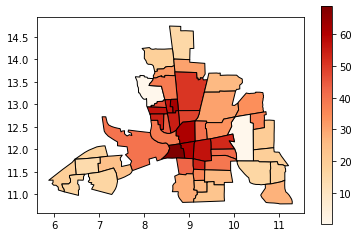
所有的49个社区沿着白色到深红色的渐变着色,但人眼在比较彼此距离较远的形状颜色时可能会感到困难。在这种情况下,特别难以对用米色着色的外围地区进行排名。
相反,我们将在颜色区间中对它们进行分类。
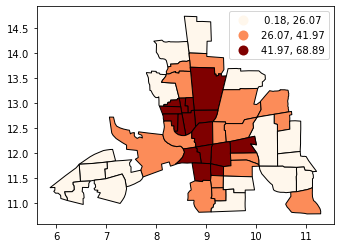
按分位数分类#
分位数将创建吸引人的地图,使每个类别中有相等数量的观察值:如果您有30个县和6个数据类别,则每个类别中将有5个县。分位数的问题是,您可能会得到数值范围非常不同的类别(例如,1-4,4-9,9-250)。
[5]:
# Splitting the data in three shows some spatial clustering around the center
tracts.plot(
column="CRIME", scheme="quantiles", k=3, cmap="OrRd", edgecolor="k", legend=True
)
[5]:
<AxesSubplot:>
[6]:
# We can also see where the top and bottom halves are located
tracts.plot(
column="CRIME", scheme="quantiles", k=2, cmap="OrRd", edgecolor="k", legend=True
)
[6]:
<AxesSubplot:>
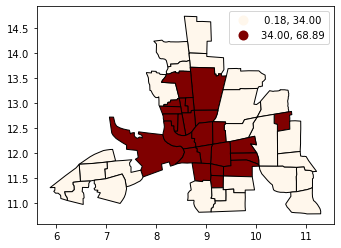
按等间隔分类#
EQUAL INTERVAL 将数据分为相等大小的类别(例如,0-10,10-20,20-30等),并且在数据通常分布在整个范围时效果最佳。注意:如果数据倾斜到一端或有一两个非常大的离群值,请避免使用相等区间。
[7]:
tracts.plot(
column="CRIME",
scheme="equal_interval",
k=4,
cmap="OrRd",
edgecolor="k",
legend=True,
)
[7]:
<AxesSubplot:>
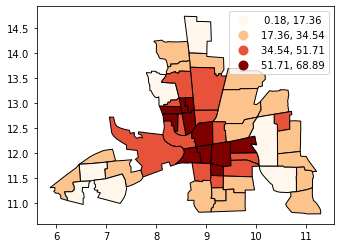
[8]:
# No legend here as we'd be out of space
tracts.plot(column="CRIME", scheme="equal_interval", k=12, cmap="OrRd", edgecolor="k")
[8]:
<AxesSubplot:>
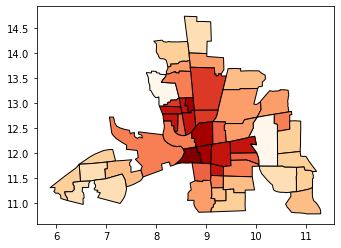
通过自然断点分类#
NATURAL BREAKS是一种“最优”分类方案,找到将使类内方差最小化和类间差异最大化的类分界线。此方法的一个缺点是每个数据集生成一个唯一的分类解决方案,如果您需要跨地图进行比较,例如在地图集或系列中(例如,1980年、1990年、2000年的每张地图各一张),您可能希望使用一个可以应用于所有地图的单一方案。
[9]:
# Compare this to the previous 3-bin figure with quantiles
tracts.plot(
column="CRIME",
scheme="natural_breaks",
k=3,
cmap="OrRd",
edgecolor="k",
legend=True,
)
[9]:
<AxesSubplot:>
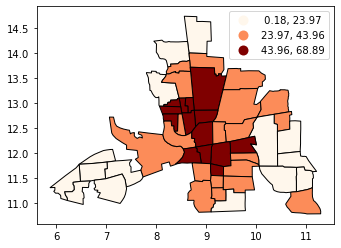
PySAL中的其他分类方案#
Geopandas仅包含在PySAL中找到的最常用分类器。为了使用其他分类器,您需要将它们作为额外的列添加到您的GeoDataFrame中。
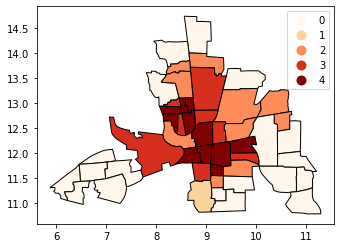
max-p 算法基于一组区域、每个区域的属性矩阵和一个最低约束条件,内生地确定区域的数量(p)。最低约束条件定义了每个区域内变量必须达到的最小边界;例如,一个约束可能是每个区域必须有的最少人口。max-p 进一步对区域内的区域强制执行连通性约束。
[10]:
def max_p(values, k):
"""
Given a list of values and `k` bins,
returns a list of their Maximum P bin number.
"""
from mapclassify import MaxP
binning = MaxP(values, k=k)
return binning.yb
tracts["Max_P"] = max_p(tracts["CRIME"].values, k=5)
tracts.head()
[10]:
| 面积 | 周长 | COLUMBUS_ | COLUMBUS_I | POLYID | 邻域 | HOVAL | INC | 犯罪 | 开放 | ... | X | Y | NSA | NSB | 东西 | CP | 千 | NEIGNO | 几何 | Max_P | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.309441 | 2.440629 | 2 | 5 | 1 | 5 | 80.467003 | 19.531 | 15.725980 | 2.850747 | ... | 38.799999 | 44.070000 | 1.0 | 1.0 | 1.0 | 0.0 | 1000.0 | 1005.0 | 多边形 ((8.62413 14.23698, 8.55970 14.74245, ... | 0 |
| 1 | 0.259329 | 2.236939 | 3 | 1 | 2 | 1 | 44.567001 | 21.232 | 18.801754 | 5.296720 | ... | 35.619999 | 42.380001 | 1.0 | 1.0 | 0.0 | 0.0 | 1000.0 | 1001.0 | POLYGON ((8.25279 14.23694, 8.28276 14.22994, ... | 0 |
| 2 | 0.192468 | 2.187547 | 4 | 6 | 3 | 6 | 26.350000 | 15.956 | 30.626781 | 4.534649 | ... | 39.820000 | 41.180000 | 1.0 | 1.0 | 1.0 | 0.0 | 1000.0 | 1006.0 | 多边形 ((8.65331 14.00809, 8.81814 14.00205, ... | 2 |
| 3 | 0.083841 | 1.427635 | 5 | 2 | 4 | 2 | 33.200001 | 4.477 | 32.387760 | 0.394427 | ... | 36.500000 | 40.520000 | 1.0 | 1.0 | 0.0 | 0.0 | 1000.0 | 1002.0 | POLYGON ((8.45950 13.82035, 8.47341 13.83227, ... | 2 |
| 4 | 0.488888 | 2.997133 | 6 | 7 | 5 | 7 | 23.225000 | 11.252 | 50.731510 | 0.405664 | ... | 40.009998 | 38.000000 | 1.0 | 1.0 | 1.0 | 0.0 | 1000.0 | 1007.0 | 多边形 ((8.68527 13.63952, 8.67758 13.72221, ... | 3 |
5 行 × 22 列
[11]:
tracts.plot(column="Max_P", cmap="OrRd", edgecolor="k", categorical=True, legend=True)
[11]:
<AxesSubplot:>
[ ]: