qml.fourier¶
概述¶
该模块包含用于分析量子电路的傅里叶表示的函数。
函数¶
|
计算简单量子电路的傅里叶表示的频谱,忽略经典预处理。 |
|
计算一个 \(2\pi\) 周期函数的前 \(2d+1\) 个傅里叶系数,其中 \(d\) 是傅里叶频谱中所需的最高频率(度数)。 |
|
提取输入编码门对量子电路的整体傅里叶表示贡献的频率。 |
|
连接属于同一输入的两个频率集。 |
|
计算量子电路的傅里叶表示的频谱,包括经典预处理。 |
|
沿着单个参数方向重构期望值 QNode。 |
可视化¶
可以在 fourier.visualize 子模块中找到可视化傅里叶表示的工具。这需要安装 matplotlib 包。
|
将一组傅里叶系数绘制为条形图。 |
|
绘制一组傅里叶系数列表的箱型图。 |
|
在复平面上绘制一组或多组系数的列表,适用于一维或二维函数。 |
|
在径向图上以箱线图的形式绘制一组傅里叶系数的列表。 |
|
将一组傅里叶系数的列表绘制为小提琴图。 |
量子电路的傅里叶表示¶
考虑一个依赖于参数向量 \(x\) 且长度为 \(N\) 的量子电路。该电路涉及某些单位操作的应用 \(U(x)\),然后测量一个可观察量 \(\hat{O}\)。从解析上看,期望值为
该输出仅仅是一个函数 \(f(x) = \langle \psi(x) \vert \hat{O} \vert \psi (x)\rangle\)。值得注意的是,它是参数的周期函数,因此可以表示为多维傅里叶级数:
其中 \(n_i\) 是整数值频率,\(\Omega_i\) 是可用整数频率的集合,而\(c_{n_1,\ldots,n_N}\) 是傅里叶系数。
作为一个简单的例子,考虑下面的 simple_circuit,它是一个单一参数的函数。
import pennylane as qml
from pennylane import numpy as np
dev = qml.device('default.qubit', wires=2)
@qml.qnode(dev)
def simple_circuit(x):
qml.RX(x[0], wires=0)
qml.RY(x[0], wires=1)
qml.CNOT(wires=[1, 0])
return qml.expval(qml.PauliZ(0))
我们可以从数学上计算出这个函数的期望值为 \(\langle Z \rangle = 0.5 + 0.5 \cos(2x)\)。因此,这个函数的傅里叶系数为 \(c_0 = 0.5\),\(c_1 = c^*_{-1} = 0\),和 \(c_2 = c^*_{-2} = 0.25\)。
PennyLane fourier 模块使得计算傅里叶系数 \(c_{n_1,\dots, n_N}\) 的值成为可能。系数的知识,进而非零系数的频率谱,对于量子电路的表达能力研究至关重要,如在 Schuld,
Sweke 和 Meyer (2020) 以及 Vidal 和
Theis, 2019 中描述的那样——可用于量子模型的系数越多,该模型能够表示的函数类就越大,潜在地为量子机器学习应用提供更大的效用。
计算电路支持的频率¶
对于某些电路,频谱 \(\Omega_j\) 的信息可以仅通过编码对应输入 \(x_j\) 的门的结构推导出来(例如,参见 Schuld, Sweke, and Meyer (2020))。更具体地说,如果所有输入编码门的形式为 \(e^{-ix_j G}\),其中 \(G\) 是一个“生成”该操作的厄米算子,我们可以推导出可以理论上出现在 \(\Omega_j\) 中的最大频率集合。根据电路中的非输入编码门,这些理论上支持的频率中可能会有一些最终具有消失的傅里叶系数,\(\Omega_j\) 实际上会变得更小。然而,基于输入编码策略的估计仍然可以帮助理解一种类型的 ansatz 的潜在表达能力。
可以使用circuit_spectrum()函数计算理论上支持的频率。为了标记哪些门编码输入(例如,哪些仅用于可训练参数),我们必须给输入编码门一个id:
import pennylane as qml
dev = qml.device('default.qubit', wires=2)
@qml.qnode(dev)
def simple_circuit_marked(x):
qml.RX(x[0], wires=0, id="x")
qml.RY(x[0], wires=1, id="x")
qml.CNOT(wires=[1, 0])
return qml.expval(qml.PauliZ(0))
我们可以计算输入编码门支持的频率,如下所示:
>>> from pennylane.fourier import circuit_spectrum
>>> freqs = circuit_spectrum(simple_circuit_marked)([0.1])
>>> for k, v in freqs.items():
>>> print(k, ":", v)
x : [-2.0, -1.0, 0.0, 1.0, 2.0]
注意
某些编码门类型可能会产生非整数值的频率。在这种情况下,circuit_spectrum() 函数计算形式为 傅里叶和 的频率集 \(\Omega_j\)
与 \(\omega \in \mathbb{R}\) 一样。与其他任何函数一样,这样的和可以转化为一个适当的傅里叶级数,但从非整数值到整数值频率的映射并不总是简单。
计算傅里叶系数¶
为了更准确地描述量子电路的傅里叶级数表示,我们必须计算傅里叶系数 \(c_{n_1,\ldots,n_N}\)。这通过在 coefficients() 函数中使用数值方法来完成:
>>> from pennylane.fourier import coefficients
>>> coeffs = coefficients(simple_circuit, 1, 2)
>>> print(np.round(coeffs, decimals=4))
[0.5 +0.j 0. -0.j 0.25+0.j 0.25+0.j 0. -0.j]
coefficients() 函数的输入是
一个函数或包含变分电路的QNode,用于计算傅里叶系数,
输入向量的长度,并且
用于计算系数的最大频率(也称为度)。
在内部,系数的计算使用了NumPy的 离散傅里叶变换 函数。因此,输出中系数的顺序遵循标准输出顺序,即 \([c_0, c_1, c_2, c_{-2}, c_{-1}]\),对于多维情况也是如此。这里使用的归一化约定对应于 norm="forward" 选项,即,对于大小为 \(N\) 的数组,傅里叶变换的结果会重新缩放为 \(1/N\),而逆傅里叶变换则保持不变。
有关系数计算的更多细节和示例,请参见coefficients()的文档。
傅里叶系数可视化¶
傅里叶模块的一个关键应用是分析量子电路家族的表达能力。量子电路的傅里叶表示中的频率集合可以用来表征参数化电路所产生的函数类。例如,如果一个嵌入导致一个具有少量低阶频率的傅里叶表示,那么使用该嵌入的量子电路只能表达相对简单的周期函数。
傅里叶模块包含多种方法,用于可视化单个电路的傅里叶级数表示的系数,以及针对参数化电路系列的傅里叶系数分布。
注意
傅里叶系数的可视化需要 matplotlib 库。因此,可视化函数包含在子模块 pennylane.fourier.visualize 中。这些可视化函数的结构是接受 matplotlib 轴作为参数,以便额外的配置(例如添加标题、保存等)可以在函数外部进行。然而,许多图表需要特定数量的子图。下面的示例演示了每个函数应该如何创建子图。
可视化一组系数¶
虽然所有可用于可视化多组傅里叶系数的函数都可以用于单组,但用于此目的的主要工具是bar()函数。使用我们在之前示例中获得的系数,
>>> from pennylane.fourier.visualize import *
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(2, 1, sharex=True, sharey=True) # Set up the axes
>>> bar(coeffs, 1, ax)
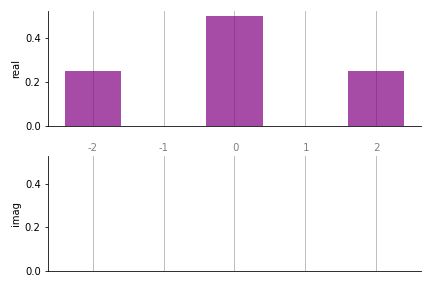
在条形图中,真实系数显示在顶部面板,复数系数显示在底部。x轴上的标签表示系数频率(对于较大的图,有时通过将 show_freqs=False 传递给绘图函数来去除这些标签是方便的)。
以下是一个更复杂的示例,演示了一些可用的额外定制选项:
from functools import partial
weights = np.array([[0.1, 0.2, 0.3], [0.4, 0.5, 0.6]])
@qml.qnode(dev)
def circuit_with_weights(w, x):
qml.RX(x[0], wires=0)
qml.RY(x[1], wires=1)
qml.CNOT(wires=[1, 0])
qml.Rot(*w[0], wires=0)
qml.Rot(*w[1], wires=1)
qml.CNOT(wires=[1, 0])
qml.RX(x[0], wires=0)
qml.RY(x[1], wires=1)
qml.CNOT(wires=[1, 0])
return qml.expval(qml.PauliZ(0))
coeffs = coefficients(partial(circuit_with_weights, weights), 2, 2)
# Number of inputs is now 2; pass custom colours as well
fig, ax = plt.subplots(2, 1, sharex=True, sharey=True, figsize=(15, 4))
bar(coeffs, 2, ax, colour_dict={"real" : "red", "imag" : "blue"})
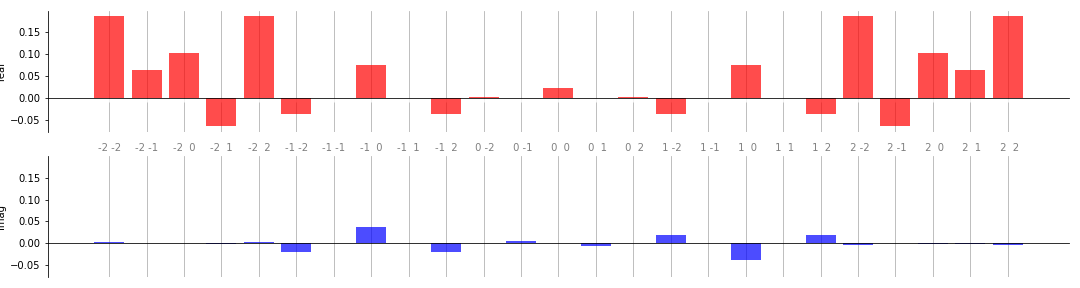
可视化多个系数集¶
假设我们不想可视化固定的weights 参数在circuit_with_weights中的傅里叶系数,而是希望在随机采样权重时观察傅里叶系数的分布。对于每个weights样本,我们会获得一组不同的系数:
coeffs = []
for _ in range(100):
weights = np.random.normal(0, 1, size=(2, 3))
c = coefficients(partial(circuit_with_weights, weights), 2, degree=2)
coeffs.append(np.round(c, decimals=8))
绘制分布的一种选择是 violin():
fig, ax = plt.subplots(2, 1, sharey=True, figsize=(15, 4))
violin(coeffs, 2, ax, show_freqs=True)
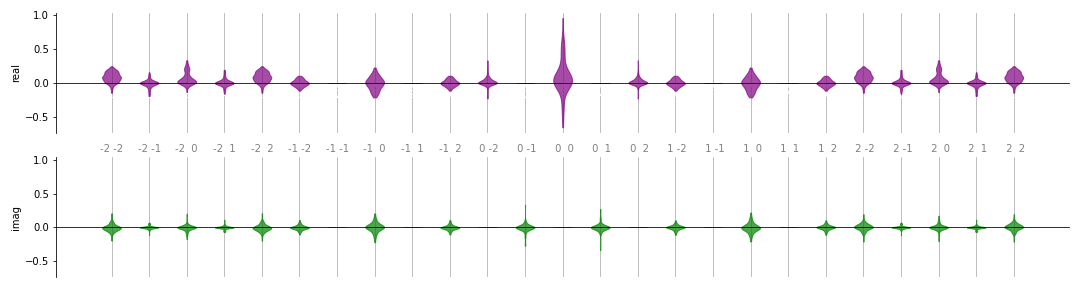
一个类似的选项是 box(),它生成相同格式的图,但使用箱形图。
可以使用radial_box()函数获得不同的视图。这个“卷起”系数到一个极坐标网格上。让我们用它来可视化与上面相同的一组系数:
# The subplot axes must be *polar* for the radial plots
fig, ax = plt.subplots(
1, 2, sharex=True, sharey=True,
subplot_kw=dict(polar=True),
figsize=(15, 8)
)
radial_box(coeffs, 2, ax, show_freqs=True, show_fliers=False)
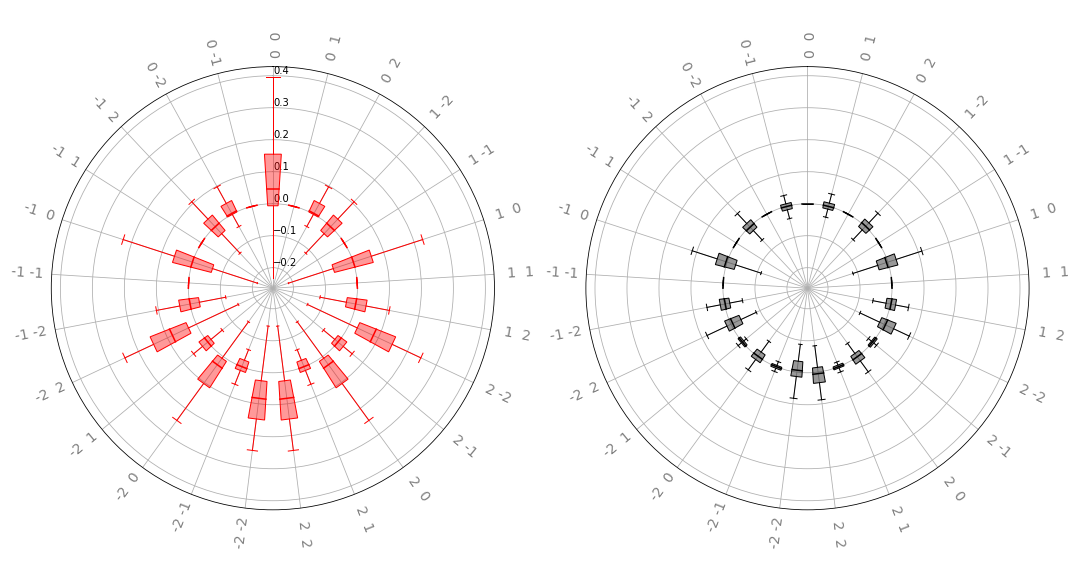
左侧图显示了分布的实部,而右侧图显示了分布的虚部,基于参数化量子电路的傅里叶系数。“轮子”上的标签代表特定频率;我们看到这与之前找到的系数一致。注意系数 \(c_0\) 出现在每个图的顶部中间;负频率从该点逆时针延伸,正频率顺时针增加。这样的图可以更紧凑地表示大量频率,而不是上面讨论的线性小提琴图和箱线图。然而,对于大量频率,建议通过设置 show_freqs=False 禁用频率标记,并隐藏箱线图的离群点,如上所述。
最后,对于1维或2维函数的特殊情况,我们可以使用
panel() 函数在复平面上绘制采样的傅里叶系数集合的分布。
# Need a grid large enough to hold all coefficients up to frequency 2
fig, ax = plt.subplots(5, 5, figsize=(12, 10), sharex=True, sharey=True)
panel(coeffs, 2, ax)
