通用混合模型
作者: Jacob Schreiber 联系方式: jmschreiber91@gmail.com
通常情况下,您拥有的数据并不能用单一的基础分布来解释。这通常是因为数据集中存在多种现象,每种现象都有其自身的基础分布。如果我们想要尝试恢复这些基础分布,就需要一个具有多个组件的模型。例如传感器读数的情况:大多数时候传感器显示无信号,但有时会检测到某些现象。若将这两种现象建模为单一分布会显得不合理,因为读数实际上来自两个截然不同的现象。
针对存在多个潜在分布的问题,一种解决方案是使用混合分布而非单一分布,这种模型通常被称为混合模型。这类组合模型通过一组更简单的分布构建出更复杂的概率分布。其中一种常见类型称为高斯混合模型,由高斯分布组成,但从数学角度而言,这些分布并不需要全部都是高斯分布。实际上,这些分布甚至不需要是简单的概率分布。
在本教程中,我们将探讨如何在pomegranate中进行混合建模,与scikit-learn的高斯混合模型实现进行对比,并探索利用概率建模可以实现的更复杂混合模型类型。
[1]:
%pylab inline
import seaborn; seaborn.set_style('whitegrid')
import torch
from pomegranate.gmm import GeneralMixtureModel
from pomegranate.distributions import *
numpy.random.seed(0)
numpy.set_printoptions(suppress=True)
%load_ext watermark
%watermark -m -n -p numpy,scipy,torch,pomegranate
Populating the interactive namespace from numpy and matplotlib
numpy : 1.23.4
scipy : 1.9.3
torch : 1.13.0
pomegranate: 1.0.0
Compiler : GCC 11.2.0
OS : Linux
Release : 4.15.0-208-generic
Machine : x86_64
Processor : x86_64
CPU cores : 8
Architecture: 64bit
一个简单的示例:高斯混合模型
让我们从一个简单的例子开始。假设我们有一个如下所示的数据集,它不是由单个数据簇组成,而是由多个数据簇构成。看起来pomegranate中实现的任何简单分布都无法完全捕捉数据中的模式。
[2]:
numpy.random.seed(0)
X = numpy.concatenate([numpy.random.normal((7, 2), 1, size=(100, 2)),
numpy.random.normal((2, 3), 1, size=(150, 2)),
numpy.random.normal((7, 7), 1, size=(100, 2))]).astype('float32')
plt.figure(figsize=(6, 5))
plt.scatter(X[:,0], X[:,1])
plt.axis(False)
plt.show()
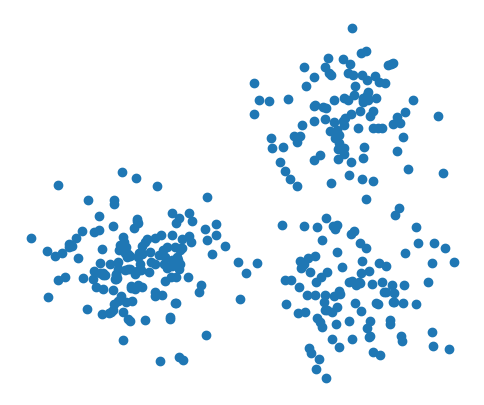
我们清楚地看到这些数据由三个簇组成。因此,与其试图寻找一个能描述该数据的复杂单一分布,我们可以将其描述为三个高斯分布的混合。就像我们可以使用fit方法初始化基本分布一样,我们也可以用该方法初始化混合模型,只需额外传入要使用的分布类型和组件数量。
[3]:
model = GeneralMixtureModel([Normal(), Normal(), Normal()], verbose=True).fit(X)
[1] Improvement: 0.216064453125, Time: 0.001145s
[2] Improvement: 0.0286865234375, Time: 0.0008411s
现在我们可以比较使用单一高斯分布与使用三个高斯模型混合时的概率密度。
[4]:
x = numpy.arange(-1, 10.1, .1)
y = numpy.arange(-1, 10.1, .1)
xx, yy = numpy.meshgrid(x, y)
x_ = numpy.array(list(zip(xx.flatten(), yy.flatten())))
p1 = Normal().fit(X).probability(x_).reshape(len(x), len(y))
p2 = model.probability(x_).reshape(len(x), len(y))
plt.figure(figsize=(10, 4))
plt.subplot(121)
plt.title("Single Gaussian", fontsize=12)
plt.contourf(xx, yy, p1, cmap='Blues')
plt.scatter(X[:,0], X[:,1], s=10)
plt.axis(False)
plt.subplot(122)
plt.title("Gaussian Mixture", fontsize=12)
plt.contourf(xx, yy, p2, cmap='Blues')
plt.scatter(X[:,0], X[:,1], s=10)
plt.axis(False)
plt.show()

不出所料,混合模型似乎能更好地捕捉数据的结构。单一高斯分布的效果非常差,其最高密度区域(最深的蓝色椭圆)内几乎没有实际数据点。相比之下,混合密度中最深的区域对应着聚类中数据点最集中的位置。
初始化与拟合
混合模型的初始化与概率分布类似:您可以传入已初始化的值,也可以不传入。如果您已经拥有概率分布,并且可选地已经知道哪些分布生成了数据的先验值,您可以将这些传入初始化并直接使用模型。
[5]:
d1 = Exponential([1.3, 3.3])
d2 = Exponential([2.2, 0.4])
model = GeneralMixtureModel([d1, d2], priors=[0.2, 0.8])
或者,如果您不知道具体的值,可以传入未初始化的分布然后进行拟合。
[6]:
d1 = Exponential()
d2 = Exponential()
X2 = torch.abs(torch.randn(15, 3))
model = GeneralMixtureModel([d1, d2], verbose=True).fit(X2)
[1] Improvement: 0.8422355651855469, Time: 0.0007176s
[2] Improvement: 0.23958969116210938, Time: 0.0005503s
[3] Improvement: 0.11565399169921875, Time: 0.0005138s
[4] Improvement: 0.07136917114257812, Time: 0.0004883s
你可以查看学习到的先验概率。
[7]:
model.priors
[7]:
Parameter containing:
tensor([0.8565, 0.1435])
训练完成后,您可以检查分布对象。
[8]:
d1.scales, d2.scales
[8]:
(Parameter containing:
tensor([0.9047, 0.9780, 0.7445]),
Parameter containing:
tensor([0.7281, 0.3527, 0.9284]))
概率与对数概率
Because mixture models themselves are technically probability distributions, it should be unsurprising that the calculation of probabilities and log probabilities are identical to that of probability distributions.
[9]:
model.log_probability(X2)
[9]:
tensor([-1.9188, -3.7001, -2.8847, -3.1817, -1.6772, -1.8678, -3.8099, -2.6887,
-3.4597, -2.5457, -1.5600, -0.9176, -1.4670, -2.0735, -3.8544])
[10]:
d1.log_probability(X2), d2.log_probability(X2)
[10]:
(tensor([-1.8586, -3.6041, -2.8660, -3.0401, -1.5696, -1.8315, -3.6627, -2.6193,
-3.3195, -2.6105, -1.8031, -1.0723, -1.7300, -2.1385, -3.7464]),
tensor([-2.3815, -4.6215, -3.0040, -5.5725, -2.8109, -2.1167, -6.7331, -3.2486,
-5.7406, -2.2277, -0.7321, -0.2995, -0.5996, -1.7543, -4.9963]))
[11]:
model.probability(X2)
[11]:
tensor([0.1468, 0.0247, 0.0559, 0.0415, 0.1869, 0.1545, 0.0222, 0.0680, 0.0314,
0.0784, 0.2101, 0.3995, 0.2306, 0.1257, 0.0212])
[12]:
d1.probability(X2), d2.probability(X2)
[12]:
(tensor([0.1559, 0.0272, 0.0569, 0.0478, 0.2081, 0.1602, 0.0257, 0.0729, 0.0362,
0.0735, 0.1648, 0.3422, 0.1773, 0.1178, 0.0236]),
tensor([0.0924, 0.0098, 0.0496, 0.0038, 0.0602, 0.1204, 0.0012, 0.0388, 0.0032,
0.1078, 0.4809, 0.7412, 0.5490, 0.1730, 0.0068]))
预测
混合模型作为聚类方法的一个关键用途是,它们可以预测哪个成分更适合每个数据点。这些方法与scikit-learn中的方法类似。首先,如果只想预测每个点的聚类标签,可以使用predict方法。让我们以高斯混合模型为例来说明。
[13]:
model = GeneralMixtureModel([Normal(), Normal(), Normal()], verbose=True).fit(X)
model.predict(X)
[1] Improvement: 0.216064453125, Time: 0.0007911s
[2] Improvement: 0.0286865234375, Time: 0.001209s
[13]:
tensor([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2])
如果您对基础概率感兴趣,即在概率分布下乘以先验并归一化的似然值(有时称为责任矩阵),您可以使用predict_proba来获取这些概率。
[14]:
model.predict_proba(X)[::15]
[14]:
tensor([[3.2331e-10, 1.0000e+00, 5.0365e-06],
[1.3677e-06, 9.9998e-01, 2.1502e-05],
[5.2814e-05, 9.9995e-01, 1.1250e-06],
[3.7857e-05, 9.9834e-01, 1.6255e-03],
[1.1822e-07, 1.0000e+00, 1.1827e-08],
[8.1322e-06, 9.8747e-01, 1.2524e-02],
[3.6977e-06, 1.0000e+00, 5.8392e-09],
[9.9969e-01, 3.0660e-04, 1.0668e-06],
[1.0000e+00, 2.7696e-07, 2.4643e-11],
[9.9968e-01, 3.2161e-04, 1.4796e-12],
[1.0000e+00, 6.9959e-09, 8.9382e-10],
[9.9966e-01, 3.3986e-04, 1.9472e-09],
[9.9987e-01, 1.2673e-04, 1.1254e-07],
[9.9992e-01, 7.5676e-05, 2.5076e-08],
[9.9969e-01, 3.0740e-04, 3.1747e-06],
[1.0000e+00, 2.4480e-08, 1.8340e-10],
[9.9986e-01, 1.2941e-04, 7.4965e-06],
[4.5694e-15, 3.9609e-07, 1.0000e+00],
[2.0310e-08, 1.0201e-02, 9.8980e-01],
[9.1368e-08, 1.3950e-01, 8.6050e-01],
[9.5965e-08, 1.5413e-05, 9.9998e-01],
[1.2553e-08, 1.0525e-04, 9.9989e-01],
[6.6068e-06, 9.7937e-03, 9.9020e-01],
[5.7233e-13, 1.8398e-06, 1.0000e+00]])
如果您想更深入地了解,可以使用predict_log_proba方法获取对数概率——这是为了数值稳定性而进行所有计算的空间。
[15]:
model.predict_log_proba(X)[::15]
[15]:
tensor([[-2.1852e+01, -4.7684e-06, -1.2199e+01],
[-1.3502e+01, -2.2650e-05, -1.0747e+01],
[-9.8487e+00, -5.3883e-05, -1.3698e+01],
[-1.0182e+01, -1.6646e-03, -6.4219e+00],
[-1.5951e+01, 0.0000e+00, -1.8253e+01],
[-1.1720e+01, -1.2612e-02, -4.3801e+00],
[-1.2508e+01, -3.8147e-06, -1.8959e+01],
[-3.0780e-04, -8.0900e+00, -1.3751e+01],
[-2.3842e-07, -1.5099e+01, -2.4427e+01],
[-3.2187e-04, -8.0422e+00, -2.7239e+01],
[ 0.0000e+00, -1.8778e+01, -2.0836e+01],
[-3.3998e-04, -7.9870e+00, -2.0057e+01],
[-1.2684e-04, -8.9735e+00, -1.6000e+01],
[-7.5579e-05, -9.4890e+00, -1.7501e+01],
[-3.1066e-04, -8.0874e+00, -1.2660e+01],
[ 0.0000e+00, -1.7525e+01, -2.2419e+01],
[-1.3685e-04, -8.9525e+00, -1.1801e+01],
[-3.3019e+01, -1.4742e+01, -4.7684e-07],
[-1.7712e+01, -4.5853e+00, -1.0253e-02],
[-1.6208e+01, -1.9697e+00, -1.5024e-01],
[-1.6159e+01, -1.1080e+01, -1.5259e-05],
[-1.8193e+01, -9.1592e+00, -1.0514e-04],
[-1.1927e+01, -4.6260e+00, -9.8486e-03],
[-2.8189e+01, -1.3206e+01, -1.6689e-06]])
零膨胀混合模型
查看零膨胀分布的一种常见方式是将其视为混合分布,其中一个分量是狄拉克δ分布(其概率质量完全集中在零上),另一个分量可以是任意其他分布。之所以显式建模零膨胀现象,是因为有时数据中的零值并非来自被建模的主要对象。虽然pomegranate已直接实现了零膨胀分布,但也可以手动实现如下:
[16]:
p = numpy.array([30, 1, 3, 7, 8, 7, 4, 3, 2, 1, 2, 1, 1, 1])
X = numpy.random.choice(len(p), size=(500, 1), p=p/p.sum())
[17]:
d = Poisson().fit(X)
d.lambdas
[17]:
Parameter containing:
tensor([3.3220])
[18]:
model = GeneralMixtureModel([DiracDelta([1]), Poisson([1])], verbose=True).fit(X)
model.distributions[1].lambdas
[1] Improvement: 1369.84814453125, Time: 0.0006914s
[2] Improvement: 89.228271484375, Time: 0.0006466s
[3] Improvement: 0.164306640625, Time: 0.000586s
[4] Improvement: 0.0001220703125, Time: 0.0006366s
[18]:
Parameter containing:
tensor([5])
[19]:
x = numpy.arange(0, len(p)+0.1, 0.1)
y1 = d.probability(x.reshape(-1, 1))
y2 = model.distributions[1].probability(x.reshape(-1, 1))
plt.figure(figsize=(6, 3))
plt.hist(X[:,0], density=True, bins=numpy.arange(0, len(p), 1))
plt.plot(x, y1, label="Poisson")
plt.plot(x, y2, label="Poisson in Mixture")
plt.legend(loc=(1.05, 0.4))
plt.tight_layout()
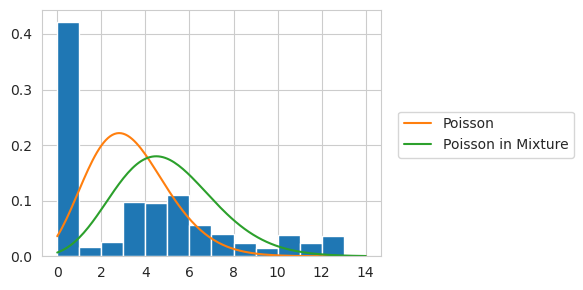
或者,我们可以使用ZeroInflated包装器来实现这一点。
[20]:
d0 = Poisson()
d = ZeroInflated(d0).fit(X)
y3 = d0.probability(x.reshape(-1, 1))
plt.figure(figsize=(6, 3))
plt.hist(X[:,0], density=True, bins=numpy.arange(0, len(p), 1))
plt.plot(x, y1, label="Poisson")
plt.plot(x, y2, label="Poisson in Mixture")
plt.plot(x, y3, label="Poisson in ZIP")
plt.legend(loc=(1.05, 0.4))
plt.tight_layout()

ZeroInflated包装器以混合模型实现所不具备的方式扩展到多元分布。简单来说,单独使用DiracDelta会给所有含有一个或多个非零值的样本赋予零概率。由于我们希望每个特征能独立评分(即矩阵中所有零值都有一定概率属于DiracDelta分量),我们需要稍微修改内部机制。以下是使用该机制的效果。
[21]:
p = numpy.array([30, 1, 3, 7, 8, 7, 4, 3, 2, 1, 2, 1, 1, 1])
X = numpy.random.choice(len(p), size=(500, 3), p=p/p.sum())
d = Poisson().fit(X)
model = GeneralMixtureModel([DiracDelta([1, 1, 1]), Poisson([1.0, 1.0, 1.0])]).fit(X)
model.distributions[1].lambdas
ZIP = ZeroInflated(Poisson()).fit(X)
d.lambdas, model.distributions[1].lambdas, ZIP.distribution.lambdas
[21]:
(Parameter containing:
tensor([3.3160, 3.1280, 3.1860]),
Parameter containing:
tensor([3.6519, 3.4448, 3.5087]),
Parameter containing:
tensor([5.7558, 5.3920, 5.3447]))