GLM: 线性回归#

本教程改编自 Thomas Wiecki 的博客文章 “推断按钮：使用 PyMC 简化贝叶斯 GLM” 。

虽然贝叶斯方法相对于频率方法的理论优势在其他地方已有广泛讨论（见下方的进一步阅读），但阻碍其更广泛采用的主要障碍是可用性。这有点讽刺，因为贝叶斯统计的美在于其通用性。频率统计涉及为特定应用提出特定的检验统计量，而在贝叶斯方法中，你可以根据认为合适的方式精确定义模型，并点击推断按钮(TM)（即运行神奇的 MCMC 采样算法）。

在过去的几十年里，一些优秀的贝叶斯软件包相继问世，包括 JAGS、BUGS 和 Stan，然而它们都是为那些非常清楚自己想构建什么模型的统计学家编写的。

不幸的是，“绝大多数统计分析不是由统计学家进行的” – 所以我们真正需要的是为科学家而非统计学家设计的工具。PyMC 使得为手头的应用构建统计模型变得简单，而不必关心各种拟合算法的实现方式。

线性回归#

在这个例子中，我们将从最简单的 GLM – 线性回归开始。通常，频率学派认为线性回归为：

\[ Y = X\beta + \epsilon \]

其中 \(Y\) 是我们想要预测的输出（或因变量），\(X\) 是我们的预测变量（或自变量），\(\beta\) 是我们想要估计的模型系数（或参数）。\(\epsilon\) 是一个误差项，假设它服从正态分布。

然后，我们可以使用普通最小二乘法 (OLS) 或最大似然估计来找到最佳拟合的 \(\beta\)。

概率重表述#

贝叶斯方法采用概率的视角来观察世界，并用概率分布来表达这个模型。我们上述的线性回归可以重新表述为：

\[ Y \sim \mathcal{N}(X \beta, \sigma^2) \]

换句话说，我们将 \(Y\) 视为一个随机变量（或随机向量），其中每个元素（数据点）都按照正态分布分布。这个正态分布的均值由我们的线性预测器提供，方差为 \(\sigma^2\)。

虽然这本质上是相同的模型，但贝叶斯估计有两个关键优势：

先验：我们可以通过对参数施加先验来量化我们可能拥有的任何先验知识。例如，如果我们认为 \(\sigma\) 可能很小，我们会选择一个在低值上具有更多概率质量的先验。
量化不确定性：我们得到的不是上述的单个 \(\beta\) 估计，而是一完整的后验分布，表明不同 \(\beta\) 值的可能性。例如，随着数据点的减少，我们对 \(\beta\) 的不确定性将非常高，这样我们得到的后验分布将会非常宽。

PyMC中的贝叶斯广义线性模型#

要开始在PyMC中构建广义线性模型，首先让我们导入所需的模块。

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import xarray as xr

from pymc import HalfCauchy, Model, Normal, sample

print(f"Running on PyMC v{pm.__version__}")

Running on PyMC v5.3.0

RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)

%config InlineBackend.figure_format = 'retina'
az.style.use("arviz-darkgrid")

生成数据#

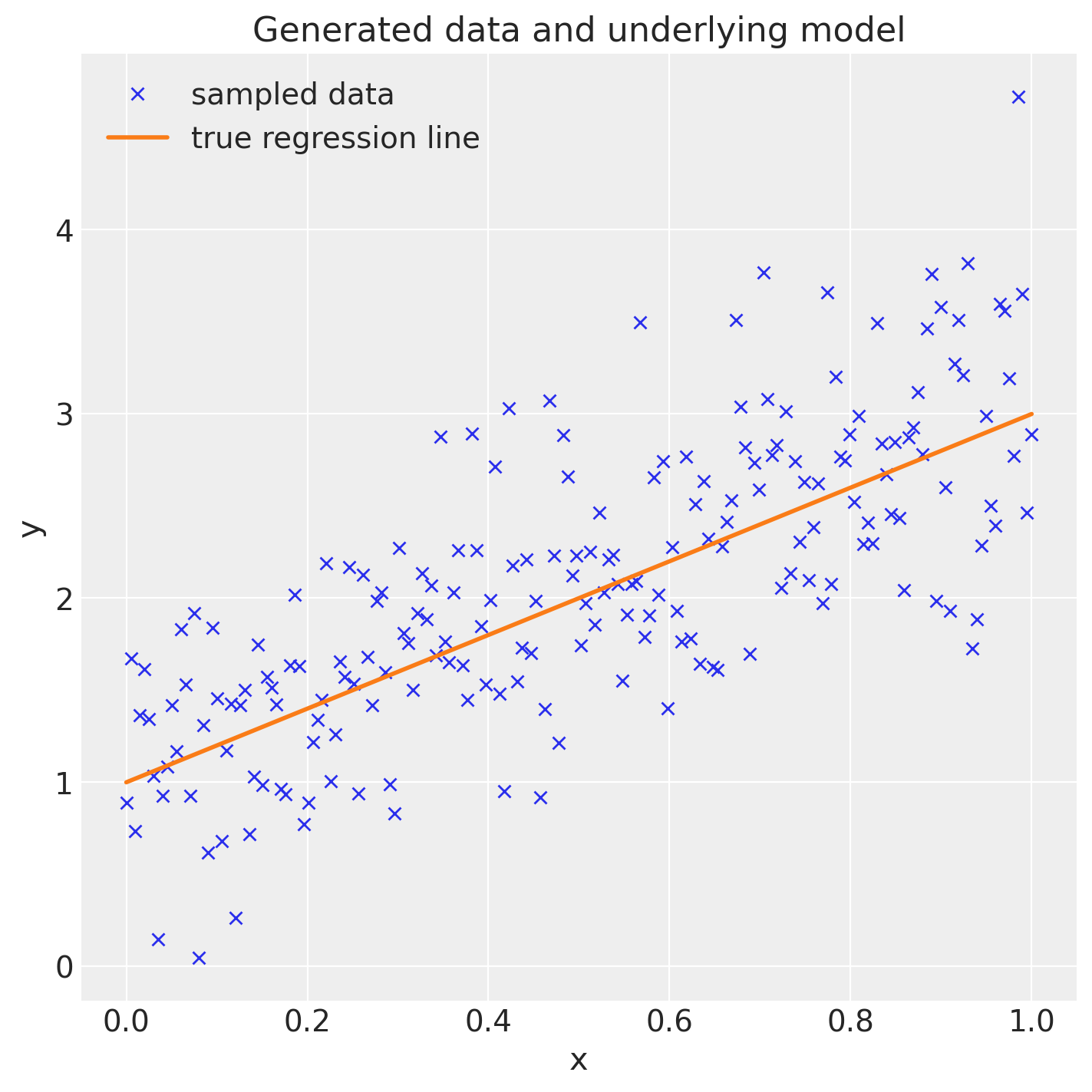
本质上，我们正在创建一个通过截距和斜率定义的回归线，并通过从均值设置为回归线的正态分布中抽样来添加数据点。

size = 200
true_intercept = 1
true_slope = 2

x = np.linspace(0, 1, size)
# y = a + b*x
true_regression_line = true_intercept + true_slope * x
# 添加噪声
y = true_regression_line + rng.normal(scale=0.5, size=size)

data = pd.DataFrame(dict(x=x, y=y))

fig = plt.figure(figsize=(7, 7))
ax = fig.add_subplot(111, xlabel="x", ylabel="y", title="Generated data and underlying model")
ax.plot(x, y, "x", label="sampled data")
ax.plot(x, true_regression_line, label="true regression line", lw=2.0)
plt.legend(loc=0);

../../_images/a75c1a386ad41bb2e448b9773a3f4d580b2cf105c21c59c4dccf48ac8eae1cf2.png

估计模型#

让我们为这些数据拟合一个贝叶斯线性回归模型。在PyMC中，模型规格在一个with表达式中进行，这称为上下文管理器。默认情况下，模型使用NUTS采样器进行拟合，从而产生一个样本轨迹，代表潜在模型参数的边际后验分布。

with Model() as model:  # 在PyMC中，模型规范被包裹在一个with语句中。
    # 定义先验
    sigma = HalfCauchy("sigma", beta=10)
    intercept = Normal("Intercept", 0, sigma=20)
    slope = Normal("slope", 0, sigma=20)

    # 定义可能性
    likelihood = Normal("y", mu=intercept + slope * x, sigma=sigma, observed=y)

    # 推断！
    # 使用NUTS采样方法抽取3000个后验样本
    idata = sample(3000)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [sigma, Intercept, slope]

100.00% [16000/16000 00:04<00:00 Sampling 4 chains, 0 divergences]

Sampling 4 chains for 1_000 tune and 3_000 draw iterations (4_000 + 12_000 draws total) took 25 seconds.

这对了解概率编程的人来说应该是相当清晰的。然而，非统计学家会知道这一切的作用吗？而且，回想一下，这只是一个非常简单的模型，在R中只需一行代码。拥有多个潜在的转换自变量、交互项或连接函数也会使这变得更加复杂且容易出错。

为了更简单，bambi库使用公式线性模型说明符来创建设计矩阵。bambi随后为每个系数添加随机变量和适当的似然函数到模型中。

如果未安装bambi，可以使用pip install bambi进行安装。

import sys

try:
    import bambi as bmb
except ImportError:
    !{sys.executable} -m pip install --upgrade bambi
    import bambi as bmb

model = bmb.Model("y ~ x", data)
idata = model.fit(draws=3000)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [y_sigma, Intercept, x]

100.00% [16000/16000 00:03<00:00 Sampling 4 chains, 0 divergences]

Sampling 4 chains for 1_000 tune and 3_000 draw iterations (4_000 + 12_000 draws total) took 22 seconds.

更简洁，但这段代码与之前的规范执行相同的功能（如果需要，我们也可以更改先验和其他所有内容）。bambi解析formulae模型字符串，为每个回归变量添加随机变量（在这种情况下是Intercept和斜率x），添加一个似然（默认情况下选择正态分布），以及所有其他变量（sigma）。最后，bambi通过使用statsmodels估计一个频率线性模型来初始化参数，以获得一个良好的起始点。

如果您不熟悉R的语法，'y ~ x'指定我们有一个输出变量y，我们希望将其估计为x的线性函数。

分析模型#

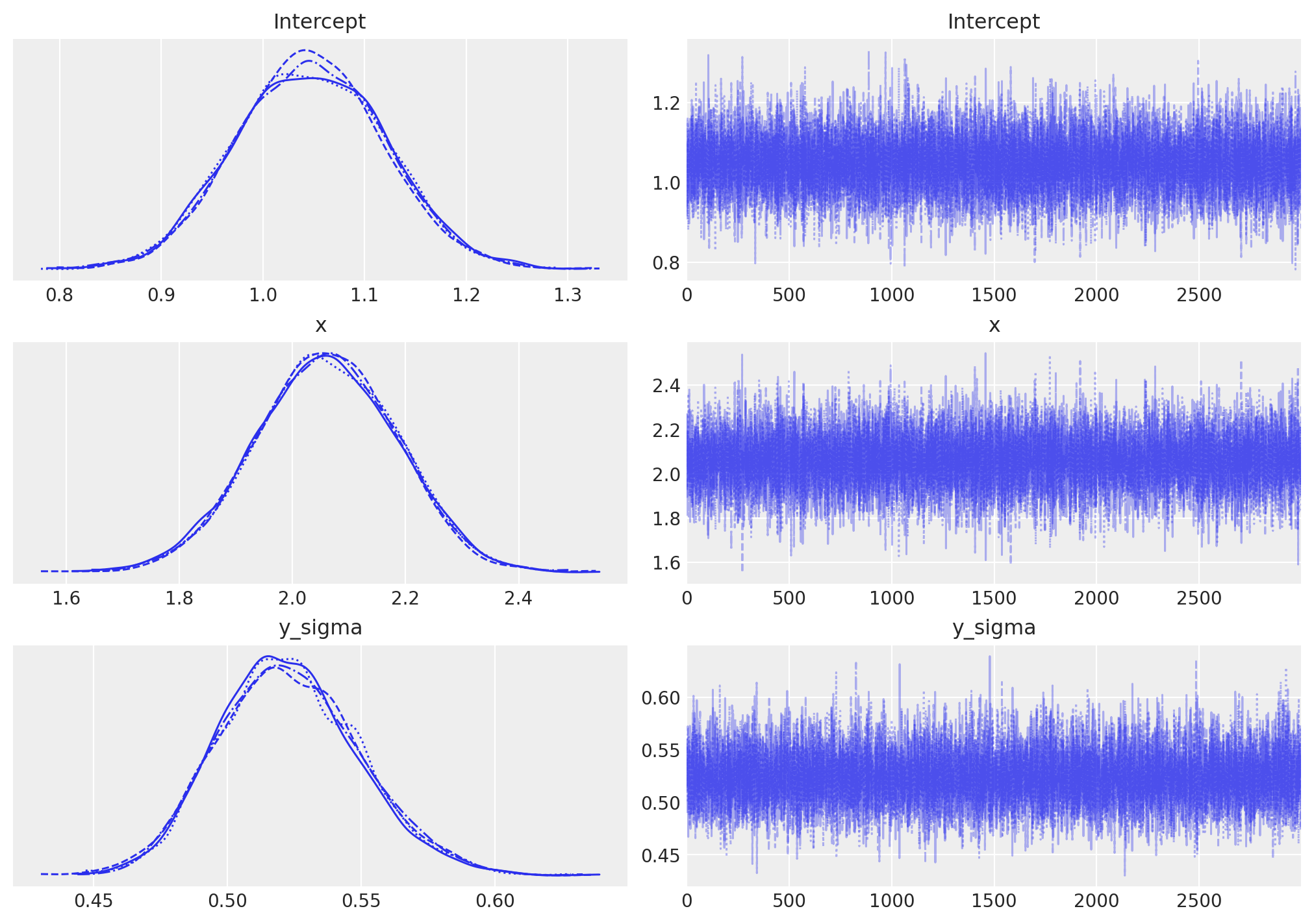
贝叶斯推断不仅仅给我们一个最佳拟合线（如最大似然估计所做），而是一个 plausible 参数的完整后验分布。让我们绘制参数的后验分布和我们抽取的个体样本。

az.plot_trace(idata, figsize=(10, 7));

../../_images/85d194a454f46fb9aa88777ac7cdfd117dc73acd83730f572756220066cafa3b.png

左侧显示了我们的边际后验 - 对于 x 轴上的每个参数值，我们在 y 轴上获得一个概率，告诉我们该参数值的可能性。

这里有几点值得注意。首先，我们对单个参数的采样链（左侧）似乎是同质和稳定的（没有大的漂移或其他奇怪的模式）。

其次，每个变量的最大后验估计（左侧分布的峰值）非常接近用于生成数据的真实参数（x 是回归系数，sigma 是我们正态分布的标准差）。

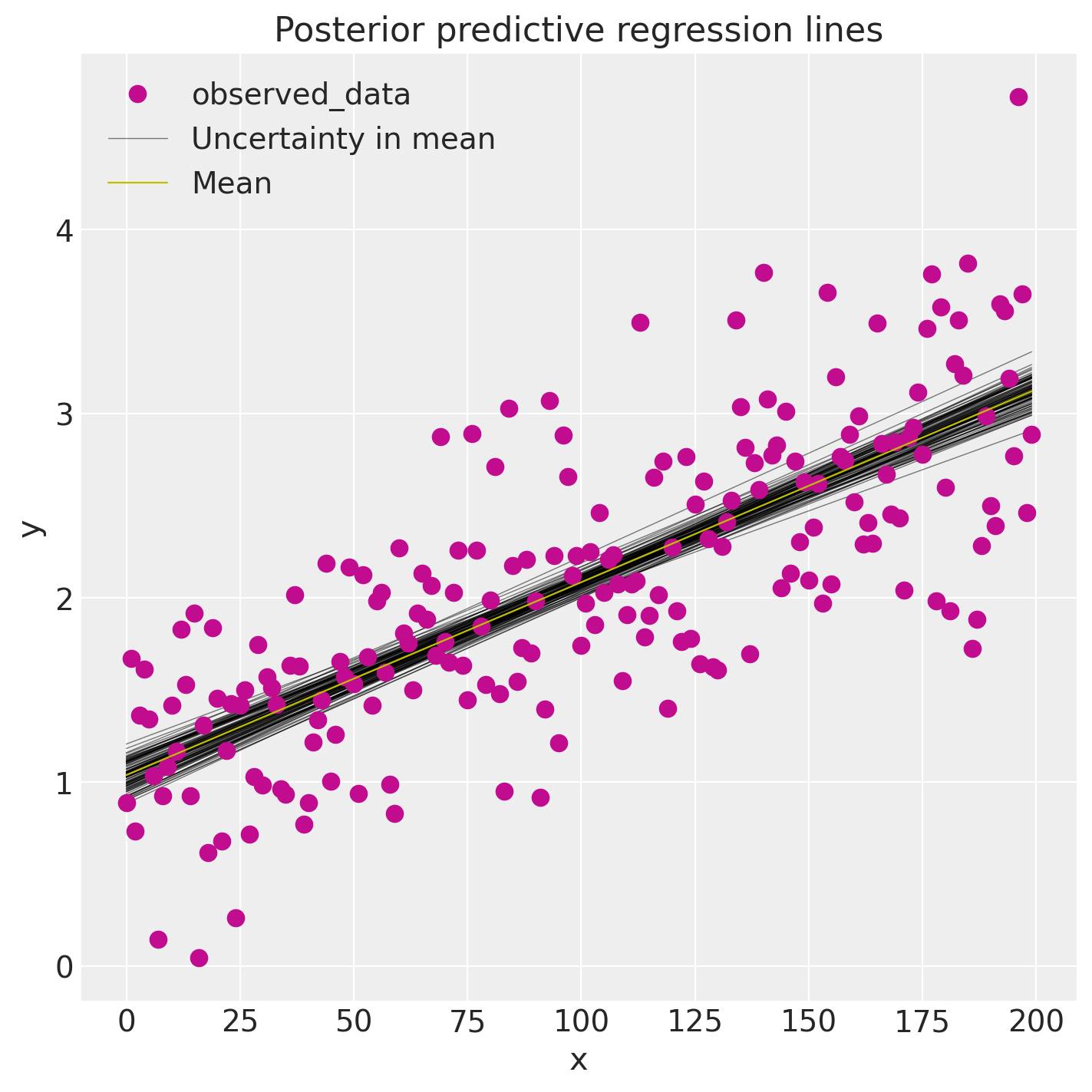
在广义线性模型中，我们并不仅仅拥有一条最佳拟合的回归线，而是许多回归线。后验预测图从后验分布中提取多个样本（截距和斜率），并为每个样本绘制一条回归线。我们可以直接使用后验样本手动生成这些回归线。

idata.posterior["y_model"] = idata.posterior["Intercept"] + idata.posterior["x"] * xr.DataArray(x)

_, ax = plt.subplots(figsize=(7, 7))
az.plot_lm(idata=idata, y="y", num_samples=100, axes=ax, y_model="y_model")
ax.set_title("Posterior predictive regression lines")
ax.set_xlabel("x");

/Users/ngeoffre/opt/anaconda3/envs/bmcp5/lib/python3.11/site-packages/arviz/plots/lmplot.py:211: UserWarning: posterior_predictive not found in idata
  warnings.warn("posterior_predictive not found in idata", UserWarning)

../../_images/7f580c1fbe39913bda784e9da7ad9fe37980faca2b2eb14a4ac25034e5ed2a16.png

正如你所看到的，我们估计的回归线与真实的回归线非常相似。但由于我们只有有限的数据，我们的估计存在不确定性，这里通过线的变动性来表示。

摘要#

可用性当前是贝叶斯统计广泛应用的一大障碍。
Bambi 允许使用从 R 中借来的便捷语法进行广义线性模型（GLM）规范。然后可以使用 pymc 进行推断。
后验预测图使我们能够评估拟合及其不确定性。

深入阅读#

为了提供更多背景，这里有一些关于贝叶斯统计的优秀资源：

由约翰·克鲁什克编写的优秀书籍《贝叶斯数据分析》。
安德鲁·盖尔曼的博客

作者：托马斯·维基

%load_ext watermark

%watermark -n -u -v -iv -w -p pytensor

Last updated: Thu Jun 01 2023

Python implementation: CPython
Python version       : 3.11.3
IPython version      : 8.13.2

pytensor: 2.11.1

xarray    : 2023.5.0
matplotlib: 3.7.1
arviz     : 0.15.1
numpy     : 1.24.3
sys       : 3.11.3 | packaged by conda-forge | (main, Apr  6 2023, 09:05:00) [Clang 14.0.6 ]
pymc      : 5.3.0
bambi     : 0.10.0
pandas    : 2.0.1

Watermark: 2.4.2