ot.lp

原始线性规划OT问题的求解器。

函数

ot.lp.center_ot_dual(alpha0, beta0, a=None, b=None)[源]

中心双重OT潜力相对于它们的权重

这个函数的主要思想是寻找独特的对偶势，使其确保某种中心化/公平性。主要思想是找到能够使源和目标的最终目标值相同的对偶势（更多细节请见下文）。这将在多次调用OT求解器时，伴随小的变化时保持稳定性。

基本上，我们为潜在的目标添加了另一个约束，这不会改变目标值，但会确保唯一性。约束如下：

\[\alpha^T \mathbf{a} = \beta^T \mathbf{b}\]

除了OT问题约束之外。

因为 \(\sum_i a_i=\sum_j b_j\) 这个可以通过在 \(\alpha_0\) 和 \(\beta_0\) 上加/减一个常数来解决。

\[ \begin{align}\begin{aligned}c &= \frac{\beta_0^T \mathbf{b} - \alpha_0^T \mathbf{a}}{\mathbf{1}^T \mathbf{b} + \mathbf{1}^T \mathbf{a}}\\\alpha &= \alpha_0 + c\\\beta &= \beta_0 + c\end{aligned}\end{align} \]
Parameters:

  • alpha0 ((ns,) numpy.ndarray, float64) – 源双重势能

  • beta0 ((nt,) numpy.ndarray, float64) – 目标双重势能

  • a ((ns,) numpy.ndarray, float64) – 源直方图（如果列表为空则为均匀权重）

  • b ((nt,) numpy.ndarray, float64) – 目标直方图（如果为空列表，则为均匀权重）

Returns:

  • alpha ((ns,) numpy.ndarray, float64) – 源中心的双重势能

  • beta ((nt,) numpy.ndarray, float64) – 目标中心的双重势能

ot.lp.check_number_threads(numThreads)[源]

检查请求的线程数量是否具有有效值。

Parameters:

numThreads (int 或 str) – 请求的线程数，必须是一个严格的正整数或者“max”或 None

Returns:

numThreads – 修正后的线程数量

Return type:

int

ot.lp.emd(a, b, M, numItermax=100000, log=False, center_dual=True, numThreads=1, check_marginals=True)[源]

解决地球搬运工距离问题并返回OT矩阵

\[ \begin{align}\begin{aligned}\gamma = \mathop{\arg \min}_\gamma \quad \langle \gamma, \mathbf{M} \rangle_F\\\text{s.t.} \ \gamma \mathbf{1} = \mathbf{a}\\ \gamma^T \mathbf{1} = \mathbf{b}\\ \gamma \geq 0\end{aligned}\end{align} \]

其中 :

  • \(\mathbf{M}\) 是度量成本矩阵

  • \(\mathbf{a}\) 和 \(\mathbf{b}\) 是样本权重

警告

请注意，\(\mathbf{M}\) 矩阵在numpy中需要是C顺序的 numpy.array，格式为float64。如果不是这种格式，将会被转换。

注意

此函数与后端兼容，可用于所有兼容后端的数组。但该算法使用C++ CPU后端，这可能导致在GPU数组上产生复制开销。

注意

该函数将把计算得到的运输计划转换为提供的输入的数据类型，优先级如下：\(\mathbf{a}\)，然后是\(\mathbf{b}\)，最后是\(\mathbf{M}\)，如果没有提供边际。转换为整数张量可能会导致精度损失。如果不希望出现这种行为，请确保提供浮点输入。

注意

如果向量 \(\mathbf{a}\) 和 \(\mathbf{b}\) 的和不相等，将会引发错误。

采用了在 [1] 中提议的算法。

Parameters:

  • a ((ns,) 数组类似, 浮点数) – 源直方图（如果空列表，则均匀权重）

  • b ((nt,) 数组类似, 浮点数) – 目标直方图（如果空列表，均匀权重）

  • M（(ns,nt) 类似数组, 浮动）– 损失矩阵（以float64类型的numpy c-顺序数组）

  • numItermax (int, 可选 (默认=100000)) – 在优化算法未收敛的情况下，停止优化前的最大迭代次数。

  • log (bool, 可选 (默认=False)) – 如果为真，返回一个包含成本和对偶变量的字典。否则仅返回最优运输矩阵。

  • center_dual (布尔值, 可选 (默认为True)) – 如果为True，使用函数 ot.lp.center_ot_dual()对双重潜力进行中心化。

  • numThreads (int 或 "max", 可选 (默认=1, 即不使用OpenMP)) – 如果使用OpenMP编译，则选择并行化的线程数。“max”选择可能的最高数量。

  • check_marginals (bool, optional (default=True)) – 如果为 True，将检查边际质量是否相等。如果为 False，跳过检查。

Returns:

  • gamma (类似数组，形状为 (ns, nt)) – 给定参数的最优运输矩阵

  • log (字典，可选) – 如果输入日志为真，将返回一个包含成本、对偶变量和退出状态的字典

示例

简单的例子，显而易见的解决方案。函数 emd 接受列表并自动转换为 numpy 数组

>>> import ot
>>> a=[.5,.5]
>>> b=[.5,.5]
>>> M=[[0.,1.],[1.,0.]]
>>> ot.emd(a, b, M)
array([[0.5, 0. ],
       [0. , 0.5]])

参考文献

另请参见

ot.bregman.sinkhorn

熵正则化最优传输

ot.optim.cg

通用正则化OT

ot.lp.emd2(a, b, M, processes=1, numItermax=100000, log=False, return_matrix=False, center_dual=True, numThreads=1, check_marginals=True)[源]

解决地球搬运工距离问题并返回损失

\[ \begin{align}\begin{aligned}\min_\gamma \quad \langle \gamma, \mathbf{M} \rangle_F\\s.t. \ \gamma \mathbf{1} = \mathbf{a}\\ \gamma^T \mathbf{1} = \mathbf{b}\\ \gamma \geq 0\end{aligned}\end{align} \]

其中 :

  • \(\mathbf{M}\) 是度量成本矩阵

  • \(\mathbf{a}\) 和 \(\mathbf{b}\) 是样本权重

注意

此函数与后端兼容，可用于所有兼容后端的数组。但该算法使用C++ CPU后端，这可能导致在GPU数组上产生复制开销。

注意

该函数将计算的运输计划和运输损失转换为提供的输入的数据类型，优先级如下：\(\mathbf{a}\)，然后 \(\mathbf{b}\)，最后在未提供边际值的情况下为 \(\mathbf{M}\)。转换为整数张量可能会导致精度的丢失。如果不希望出现这种情况，请确保提供浮点输入。

注意

如果向量 \(\mathbf{a}\) 和 \(\mathbf{b}\) 的和不相等，将会引发错误。

采用了在 [1] 中提议的算法。

Parameters:

  • a ((ns,) 数组类型, 浮动64) – 源直方图（如果是空列表则均匀权重）

  • b ((nt,) 数组样式, 浮动64) – 目标直方图（如果空列表，则为均匀权重）

  • M ((ns,nt) 数组类似, float64) – 损失矩阵（用于类型为float64的numpy c-order数组）

  • 进程 (int, 可选 (默认为1)) – 用于多重emd计算的进程数量（已弃用）

  • numItermax (int, 可选 (默认=100000)) – 在优化算法未收敛的情况下，停止优化前的最大迭代次数。

  • log (boolean, optional (default=False)) – 如果为 True，返回包含双重变量的字典。否则，仅返回最优运输成本。

  • return_matrix (boolean, 可选 (默认=False)) – 如果为真，则返回日志中的最佳运输矩阵。

  • center_dual (布尔值, 可选 (默认为True)) – 如果为True，使用函数 ot.lp.center_ot_dual()对双重潜力进行中心化。

  • numThreads (int 或 "max", 可选 (默认=1, 即不使用OpenMP)) – 如果使用OpenMP编译，则选择并行化的线程数。“max”选择可能的最高数量。

  • check_marginals (bool, optional (default=True)) – 如果为 True，将检查边际质量是否相等。如果为 False，跳过检查。

Returns:

  • W (float, array-like) – 给定参数的最优运输损失

  • log (dict) – 如果输入日志为真，则包含对偶变量和退出状态的字典

示例

简单的例子，显而易见的解决方案。函数 emd 接受列表并自动转换为 numpy 数组

>>> import ot
>>> a=[.5,.5]
>>> b=[.5,.5]
>>> M=[[0.,1.],[1.,0.]]
>>> ot.emd2(a,b,M)
0.0

参考文献

另请参见

ot.bregman.sinkhorn

熵正则化最优传输

ot.optim.cg

通用正则化OT

ot.lp.estimate_dual_null_weights(alpha0, beta0, a, b, M)[源]

估计0权重双潜力的可行值

可行值计算效率高但相对粗糙。

警告

这个函数是必要的，因为emd_c中的C++求解器会丢弃权重为零的分布中的所有样本。这意味着虽然原始变量（运输矩阵）是精确的，但求解器只会返回权重不同于零的样本上的可行对偶势能。

首先我们计算约束违规：

\[\mathbf{V} = \alpha + \beta^T - \mathbf{M}\]

接下来我们计算每行的最大违规金额 (\(\alpha\)) 和列 (\(beta\))

\[ \begin{align}\begin{aligned}\mathbf{v^a}_i = \max_j \mathbf{V}_{i,j}\\\mathbf{v^b}_j = \max_i \mathbf{V}_{i,j}\end{aligned}\end{align} \]

最后，如果违反了约束条件，我们将权重为0的对偶潜力进行更新

\[ \begin{align}\begin{aligned}\alpha_i = \alpha_i - \mathbf{v^a}_i \quad \text{ 如果 } \mathbf{a}_i=0 \text{ 并且 } \mathbf{v^a}_i>0\\\beta_j = \beta_j - \mathbf{v^b}_j \quad \text{ 如果 } \mathbf{b}_j=0 \text{ 并且 } \mathbf{v^b}_j > 0\end{aligned}\end{align} \]

最后，双重潜力通过函数 ot.lp.center_ot_dual()进行中心化。

请注意，所有这些更新并不会改变解的目标值，而是提供不违反约束的对偶势。

Parameters:

  • alpha0 ((ns,) numpy.ndarray, float64) – 源双潜能

  • beta0 ((nt,) numpy.ndarray, float64) – 目标对偶势

  • alpha0 – 源双重势能

  • beta0 – 目标双潜力

  • a ((ns,) numpy.ndarray, float64) – 源分布（如果空列表则均匀权重）

  • b ((nt,) numpy.ndarray, float64) – 目标分布（如果是空列表则为均匀权重）

  • M ((ns,nt) numpy.ndarray, float64) – 损失矩阵（按c顺序的类型为float64的数组）

Returns:

  • alpha ((ns,) numpy.ndarray, float64) – 源校正双重势能

  • beta ((nt,) numpy.ndarray, float64) – 目标校正双重势能

ot.lp.free_support_barycenter(measures_locations, measures_weights, X_init, b=None, weights=None, numItermax=100, stopThr=1e-07, verbose=False, log=None, numThreads=1)[源]

解决自由支撑（重心的位置被优化，而不是权重）Wasserstein 重心问题（即 2-Wasserstein 距离的加权 Frechet 均值），正式定义为：

\[\min_\mathbf{X} \quad \sum_{i=1}^N w_i W_2^2(\mathbf{b}, \mathbf{X}, \mathbf{a}_i, \mathbf{X}_i)\]

其中 :

  • \(w \in \mathbb{(0, 1)}^{N}\) 是 barycenter 权重，其总和为 1

  • measure_weights 表示 \(\mathbf{a}_i \in \mathbb{R}^{k_i}\): 经验度量权重（在单纯形上）

  • measures_locations 指的是 \(\mathbf{X}_i \in \mathbb{R}^{k_i, d}\): 经验测量原子的位置

  • \(\mathbf{b} \in \mathbb{R}^{k}\) 是所需的重心权重向量

这个问题在[20]（算法 2）中被考虑。以下代码有两个不同之处：

  • 我们不对权重进行优化

  • 我们不进行位置更新的线搜索，我们使用即 \(\theta = 1\) 在 [20]（算法 2）中。这可以看作是在连续设置中 [43] 提出的固定点算法的离散实现。

Parameters:

  • measures_locations (列表 的 N (k_i,d) 数组类型) – 测量支持于 \(k_i\) 位置的离散支持，在一个 d 维空间中 (\(k_i\) 对于列表的每个元素可以是不同的)

  • measures_weights (列表 的 N (k_i,) 类数组) – Numpy 数组，其中每个 numpy 数组具有 \(k_i\) 个非负值，总和为一，代表每个离散输入度量的权重

  • X_init ((k,d) 数组类型) – 重心的支持位置（在 k 个原子上）的初始化

  • b ((k,) 类似数组) – 重心权重的初始化（非负数，总和为1）

  • 权重 ((N,) 类数组) – 重心系数的初始化（非负，和为1）

  • numItermax (int, 可选) – 最大迭代次数

  • stopThr (float, 可选) – 错误的停止阈值 (>0)

  • verbose (bool, 可选) – 在迭代过程中打印信息

  • log (bool, 可选) – 如果为真，则记录日志

  • numThreads (int 或 "max", 可选 (默认=1, 即不使用OpenMP)) – 如果使用OpenMP编译，则选择并行化的线程数。“max”选择可能的最高数量。

Returns:

X – 重心的支持位置（在k个原子上）

Return type:

(k,d) 类似数组

参考文献

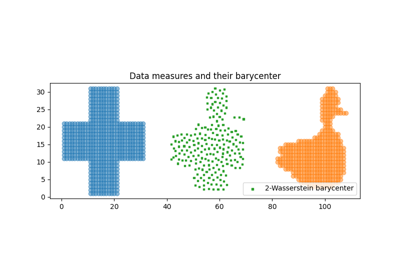
使用ot.lp.free_support_barycenter

分布的2D自由支撑Wasserstein重心

分布的2D自由支持Wasserstein重心
ot.lp.generalized_free_support_barycenter(X_list, a_list, P_list, n_samples_bary, Y_init=None, b=None, weights=None, numItermax=100, stopThr=1e-07, verbose=False, log=None, numThreads=1, eps=0)[源]

解决自由支持广义沃瑟斯坦重心问题：寻找一个重心（一个具有固定数量均匀权重的离散测度），其相应的投影符合输入测度。更正式地说：

\[\min_\gamma \quad \sum_{i=1}^p w_i W_2^2(\nu_i, \mathbf{P}_i\#\gamma)\]

其中 :

  • \(\gamma = \sum_{l=1}^n b_l\delta_{y_l}\) 是期望的重心，其中每个 \(y_l \in \mathbb{R}^d\)

  • \(\mathbf{b} \in \mathbb{R}^{n}\) 是重心所需的权重向量

  • 输入度量为 \(\nu_i = \sum_{j=1}^{k_i}a_{i,j}\delta_{x_{i,j}}\)

  • 各个\(\mathbf{a}_i \in \mathbb{R}^{k_i}\) 是相应的经验测量权重（在简单形上）

  • 每个\(\mathbf{X}_i \in \mathbb{R}^{k_i, d_i}\)是各自经验度量原子的位置

  • \(w = (w_1, \cdots w_p)\) 是重心系数（在单纯形上）

  • 每个 \(\mathbf{P}_i \in \mathbb{R}^{d, d_i}\)，并且 \(P_i\#\nu_i = \sum_{j=1}^{k_i}a_{i,j}\delta_{P_ix_{i,j}}\)

如[42]所示， 这个问题可以重写为一个Wasserstein Barycenter问题， 我们使用自由支持方法[20] （算法2）来解决。

Parameters:

  • X_list (列表 of p (k_i,d_i) 类数组) – 输入测量的离散支持：每个支持包含\(k_i\)个位置，位于一个d_i维空间中 (\(k_i\)可以对列表中的每个元素不同)

  • a_list (列表 的 p (k_i,) 数组类似) – 测量权重：每个元素是单纯形上的一个向量 (k_i)

  • P_list (列表 of p (d_i,d) 数组类似) – 每个 \(P_i\) 是一个线性映射 \(\mathbb{R}^{d} \rightarrow \mathbb{R}^{d_i}\)

  • n_samples_bary (int) – 重心点的数量

  • Y_init ((n_samples_bary,d) array-like) – 重心的支持位置初始化（在 k 原子上）

  • b ((n_samples_bary,) array-like) – 重心测量的权重初始化（在简单形体上）

  • weights ((p,) array-like) – 重心系数的初始化（在单纯形上）

  • numItermax (int, 可选) – 最大迭代次数

  • stopThr (float, 可选) – 错误的停止阈值 (>0)

  • verbose (bool, 可选) – 在迭代过程中打印信息

  • log (bool, 可选) – 如果为真，则记录日志

  • numThreads (int 或 "max", 可选 (默认=1, 即不使用OpenMP)) – 如果使用OpenMP编译，则选择并行化的线程数。“max”选择可能的最高数量。

  • eps (变量矩阵反演的稳定性系数 ) – 如果 \(\mathbf{P}_i^T\) 矩阵无法生成 \(\mathbb{R}^d\)，则该问题是未定义的，矩阵反演将失败。在这种情况下，可以设置 eps=1e-8 并仍然得到一个解（这可能意义不大）

Returns:

Y – 重心的支持位置（在 n_samples_bary 原子上）

Return type:

(n_samples_bary,d) 类数组

参考文献

使用 ot.lp.generalized_free_support_barycenter 的示例

广义沃萨斯坦质心演示

广义瓦瑟斯坦重心演示
ot.lp.barycenter(A, M, weights=None, verbose=False, log=False, solver='highs-ipm')[源]

计算分布 A 的 Wasserstein 重心

该函数解决以下优化问题 [16]：

\[\mathbf{a} = arg\min_\mathbf{a} \sum_i W_{1}(\mathbf{a},\mathbf{a}_i)\]

其中 :

  • \(W_1(\cdot,\cdot)\) 是 Wasserstein 距离（见 ot.emd.sinkhorn）

  • \(\mathbf{a}_i\) 是矩阵 \(\mathbf{A}\) 列中的训练分布

线性程序是使用scipy.optimize中的内部点求解器解决的。 如果安装了cvxopt求解器，它可以使用cvxopt

注意，这个问题在内存和计算时间上无法很好地扩展。

Parameters:

  • A (np.ndarray (d,n)) – n个大小为d的训练分布a_i

  • M (np.ndarray (d,d)) – OT的损失矩阵

  • reg (float) – 正则化项 >0

  • weights (np.ndarray (n,)) – 每个直方图 a_i 在简单形上的权重（重心坐标）

  • verbose (bool, 可选) – 在迭代过程中打印信息

  • log (bool, 可选) – 如果为真，则记录日志

  • solver (string, optional) – 使用的求解器，默认值为‘interior-point’，使用来自 scipy.optimize 的 lp 求解器。None，或 ‘glpk’ 或 ‘mosek’ 使用来自 cvxopt 的求解器。

Returns:

  • a ((d,) ndarray) – Wasserstein 重心

  • log (dict) – 仅在参数中 log==True 时返回日志字典

参考文献

ot.lp.binary_search_circle(u_values, v_values, u_weights=None, v_weights=None, p=1, Lm=10, Lp=10, tm=-1, tp=1, eps=1e-06, require_sort=True, log=False)[源]

使用在[44]中提出的二分搜索算法计算圆上的Wasserstein距离。样本需要在\(S^1\cong [0,1[\)中。如果它们在\(\mathbb{R}\)上，将取模1的值。如果值在\(S^1\subset\mathbb{R}^2\)上，需要先使用例如atan2函数找到坐标。

\[W_p^p(u,v) = \inf_{\theta\in\mathbb{R}}\int_0^1 |F_u^{-1}(q) - (F_v-\theta)^{-1}(q)|^p\ \mathrm{d}q\]

其中：

  • \(F_u\) 和 \(F_v\) 分别是 \(u\) 和 \(v\) 的累积分布函数

对于值 \(x=(x_1,x_2)\in S^1\)，需要首先获取它们的坐标，方法是

\[u = \frac{\pi + \mathrm{atan2}(-x_2,-x_1)}{2\pi}\]

使用例如 ot.utils.get_coordinate_circle(x)

该函数在后台运行，但不支持tensorflow和jax。

Parameters:

  • u_values (ndarray, shape (n, ...)) – 源域中的样本（坐标在 [0,1[）

  • v_values (ndarray, shape (n, ...)) – 目标领域中的样本（坐标在 [0,1[ 上）

  • u_weights (ndarray, shape (n, ...), optional) – 源领域中的样本权重

  • v_weights (ndarray, shape (n, ...), 可选) – 目标域中的样本权重

  • p (float, 可选 (默认=1)) – 用于计算Wasserstein距离的功率p

  • Lm (int, 可选) – 下界 dC

  • Lp (int, 可选) – 上限 dC

  • tm (float, 可选) – 下限 theta

  • tp (float, 可选) – 上界 theta

  • eps (float, 可选) – 停止条件

  • require_sort (bool, 可选) – 如果为 True，则对值进行排序。

  • log (bool, 可选) – 如果为 True，还返回最优的 theta

Returns:

  • loss (float) – 与最优运输相关的成本

  • log (dict, optional) – 仅在参数中log==True时返回的日志字典

示例

>>> u = np.array([[0.2,0.5,0.8]])%1
>>> v = np.array([[0.4,0.5,0.7]])%1
>>> binary_search_circle(u.T, v.T, p=1)
array([0.1])

参考文献

ot.lp.dmmot_monge_1dgrid_loss(A, verbose=False, log=False)[源]

计算分布A的离散多边际最优运输。

该函数作用于支持为实数的实线上的分布。

该算法同时解决原始和对偶d-MMOT程序，以生成最优运输计划以及总（最小）成本。成本是一个基础成本，解决方案与所需的Monge成本无关。

该算法接受 \(d\) 分布（即直方图） \(a_{1}, \ldots, a_{d} \in \mathbb{R}_{+}^{n}\)，且所有 \(j \in[d]\) 的 \(e^{\prime} a_{j}=1\)。尽管算法声明所有直方图具有相同数量的箱子，但该算法可以轻松适应接受 \(a_{i} \in \mathbb{R}_{+}^{n_{i}}\) 作为输入，其中 \(n_{i} \neq n_{j}\) [50]。

该函数解决以下优化问题[51]：

\[\begin{split}\begin{align}\begin{aligned} \underset{\gamma\in\mathbb{R}^{n^{d}}_{+}} {\textrm{min}} \sum_{i_1,\ldots,i_d} c(i_1,\ldots, i_d)\, \gamma(i_1,\ldots,i_d) \quad \textrm{s.t.} \sum_{i_2,\ldots,i_d} \gamma(i_1,\ldots,i_d) &= a_1(i_i), (\forall i_1\in[n])\\ \qquad\vdots\\ \sum_{i_1,\ldots,i_{d-1}} \gamma(i_1,\ldots,i_d) &= a_{d}(i_{d}), (\forall i_d\in[n]). \end{aligned} \end{align}\end{split}\]
Parameters:

  • A (nx.ndarray, shape (dim, n_hists)) – 输入的ndarray，包含d维中n个bins的分布。

  • verbose (bool, 可选) – 如果为真，执行过程中打印调试信息。默认=False。

  • log (bool, 可选) – 如果为 True，则记录日志。默认值为 False。

Returns:

  • obj (float) – 在解处评估的原始目标函数的值。

  • log (dict) – 包含离散mmot问题日志的字典： - ‘A’: 一个将索引元组映射到相应原始变量的字典。元组是算法中设置为其最小值的条目的索引。 - ‘primal objective’: 一个浮点数，在解处评估的目标函数的值。 - ‘dual’: 一个数组列表，输入数组对应的对偶变量。列表的第i个元素是对应于输入数组第i个维度的对偶变量。 - ‘dual objective’: 一个浮点数，在解处评估的对偶目标函数的值。

参考文献

另请参见

ot.lp.dmmot_monge_1dgrid_optimize

优化d维地球

移动器

ot.lp.dmmot_monge_1dgrid_optimize(A, niters=100, lr_init=1e-05, lr_decay=0.995, print_rate=100, verbose=False, log=False)[源]

使用梯度下降法最小化d维EMD。

离散多边际最优运输 (d-MMOT)：设 \(a_1, \ldots, a_d\in\mathbb{R}^n_{+}\) 为离散概率分布。这里，d-MMOT 是线性规划，

\[\begin{split}\begin{align}\begin{aligned} \underset{x\in\mathbb{R}^{n^{d}}_{+}} {\textrm{最小化}} \sum_{i_1,\ldots,i_d} c(i_1,\ldots, i_d)\, x(i_1,\ldots,i_d) \quad \textrm{满足} \sum_{i_2,\ldots,i_d} x(i_1,\ldots,i_d) &= a_1(i_i), (\forall i_1\in[n])\\ \qquad\vdots\\ \sum_{i_1,\ldots,i_{d-1}} x(i_1,\ldots,i_d) &= a_{d}(i_{d}), (\forall i_d\in[n]). \end{aligned} \end{align}\end{split}\]

d-MMOT问题的对偶线性规划是：

\[\underset{z_j\in\mathbb{R}^n, j\in[d]}{\textrm{最大化}}\qquad\sum_{j} a_j'z_j\qquad \textrm{限制条件}\qquad z_{1}(i_1)+\cdots+z_{d}(i_{d}) \leq c(i_1,\ldots,i_{d}),\]

约束中的索引包括所有 \(i_j\in[n]\)， :math: jin[d]。用 \(\phi(a_1,\ldots,a_d)\) 表示 d-MMOT 问题中线性规划的最优目标值。设 \(z^*\) 为对偶问题的最优解。然后，

\[\begin{split}\begin{align} \nabla \phi(a_1,\ldots,a_{d}) &= z^*, ~~\text{对于任何 $t\in \mathbb{R}$,}~~ \phi(a_1,a_2,\ldots,a_{d}) = \sum_{j}a_j' (z_j^* + t\, \eta), \nonumber \\ \text{其中 } \eta &:= (z_1^{*}(n)\,e, z^*_1(n)\,e, \cdots, z^*_{d}(n)\,e) \end{align}\end{split}\]

使用这些算法自然提供的双变量在 ot.lp.dmmot_monge_1dgrid_loss 中，梯度步骤使每个输入分布移动，以最小化它们的 d-mmot 距离。

Parameters:

  • A (nx.ndarray, shape (dim, n_hists)) – 输入的ndarray，包含d维中n个bins的分布。

  • niters (int, 可选 (默认=100)) – 优化算法的最大迭代次数。

  • lr_init (float, 可选 (默认=1e-5)) – 优化算法的初始学习率（步长）。

  • lr_decay (float, 可选 (默认=0.995)) – 每次迭代中的学习率衰减率。

  • print_rate (int, 可选 (默认=100)) – 在优化算法过程中打印目标值和梯度范数的频率。

  • verbose (bool, 可选) – 如果为真，执行过程中打印调试信息。默认=False。

  • log (bool, 可选) – 如果为 True，则记录日志。默认值为 False。

Returns:

  • a (ndarray列表，每个形状为 (n,)) – 作为 n 个近似重心的最佳解决方案列表，每个重心长度为 vecsize。

  • log (字典) – 仅在参数中 log==True 时返回日志字典

参考文献

另请参见

ot.lp.dmmot_monge_1dgrid_loss

d-维地球搬运工求解器

ot.lp.emd(a, b, M, numItermax=100000, log=False, center_dual=True, numThreads=1, check_marginals=True)[源]

解决地球搬运工距离问题并返回OT矩阵

\[ \begin{align}\begin{aligned}\gamma = \mathop{\arg \min}_\gamma \quad \langle \gamma, \mathbf{M} \rangle_F\\\text{s.t.} \ \gamma \mathbf{1} = \mathbf{a}\\ \gamma^T \mathbf{1} = \mathbf{b}\\ \gamma \geq 0\end{aligned}\end{align} \]

其中 :

  • \(\mathbf{M}\) 是度量成本矩阵

  • \(\mathbf{a}\) 和 \(\mathbf{b}\) 是样本权重

警告

请注意，\(\mathbf{M}\) 矩阵在numpy中需要是C顺序的 numpy.array，格式为float64。如果不是这种格式，将会被转换。

注意

此函数与后端兼容，可用于所有兼容后端的数组。但该算法使用C++ CPU后端，这可能导致在GPU数组上产生复制开销。

注意

该函数将把计算得到的运输计划转换为提供的输入的数据类型，优先级如下：\(\mathbf{a}\)，然后是\(\mathbf{b}\)，最后是\(\mathbf{M}\)，如果没有提供边际。转换为整数张量可能会导致精度损失。如果不希望出现这种行为，请确保提供浮点输入。

注意

如果向量 \(\mathbf{a}\) 和 \(\mathbf{b}\) 的和不相等，将会引发错误。

采用了在 [1] 中提议的算法。

Parameters:

  • a ((ns,) 数组类似, 浮点数) – 源直方图（如果空列表，则均匀权重）

  • b ((nt,) 数组类似, 浮点数) – 目标直方图（如果空列表，均匀权重）

  • M（(ns,nt) 类似数组, 浮动）– 损失矩阵（以float64类型的numpy c-顺序数组）

  • numItermax (int, 可选 (默认=100000)) – 在优化算法未收敛的情况下，停止优化前的最大迭代次数。

  • log (bool, 可选 (默认=False)) – 如果为真，返回一个包含成本和对偶变量的字典。否则仅返回最优运输矩阵。

  • center_dual (布尔值, 可选 (默认为True)) – 如果为True，使用函数 ot.lp.center_ot_dual()对双重潜力进行中心化。

  • numThreads (int 或 "max", 可选 (默认=1, 即不使用OpenMP)) – 如果使用OpenMP编译，则选择并行化的线程数。“max”选择可能的最高数量。

  • check_marginals (bool, optional (default=True)) – 如果为 True，将检查边际质量是否相等。如果为 False，跳过检查。

Returns:

  • gamma (类似数组，形状为 (ns, nt)) – 给定参数的最优运输矩阵

  • log (字典，可选) – 如果输入日志为真，将返回一个包含成本、对偶变量和退出状态的字典

示例

简单的例子，显而易见的解决方案。函数 emd 接受列表并自动转换为 numpy 数组

>>> import ot
>>> a=[.5,.5]
>>> b=[.5,.5]
>>> M=[[0.,1.],[1.,0.]]
>>> ot.emd(a, b, M)
array([[0.5, 0. ],
       [0. , 0.5]])

参考文献

另请参见

ot.bregman.sinkhorn

熵正则化最优传输

ot.optim.cg

通用正则化OT

ot.lp.emd2(a, b, M, processes=1, numItermax=100000, log=False, return_matrix=False, center_dual=True, numThreads=1, check_marginals=True)[源]

解决地球搬运工距离问题并返回损失

\[ \begin{align}\begin{aligned}\min_\gamma \quad \langle \gamma, \mathbf{M} \rangle_F\\s.t. \ \gamma \mathbf{1} = \mathbf{a}\\ \gamma^T \mathbf{1} = \mathbf{b}\\ \gamma \geq 0\end{aligned}\end{align} \]

其中 :

  • \(\mathbf{M}\) 是度量成本矩阵

  • \(\mathbf{a}\) 和 \(\mathbf{b}\) 是样本权重

注意

此函数与后端兼容，可用于所有兼容后端的数组。但该算法使用C++ CPU后端，这可能导致在GPU数组上产生复制开销。

注意

该函数将计算的运输计划和运输损失转换为提供的输入的数据类型，优先级如下：\(\mathbf{a}\)，然后 \(\mathbf{b}\)，最后在未提供边际值的情况下为 \(\mathbf{M}\)。转换为整数张量可能会导致精度的丢失。如果不希望出现这种情况，请确保提供浮点输入。

注意

如果向量 \(\mathbf{a}\) 和 \(\mathbf{b}\) 的和不相等，将会引发错误。

采用了在 [1] 中提议的算法。

Parameters:

  • a ((ns,) 数组类型, 浮动64) – 源直方图（如果是空列表则均匀权重）

  • b ((nt,) 数组样式, 浮动64) – 目标直方图（如果空列表，则为均匀权重）

  • M ((ns,nt) 数组类似, float64) – 损失矩阵（用于类型为float64的numpy c-order数组）

  • 进程 (int, 可选 (默认为1)) – 用于多重emd计算的进程数量（已弃用）

  • numItermax (int, 可选 (默认=100000)) – 在优化算法未收敛的情况下，停止优化前的最大迭代次数。

  • log (boolean, optional (default=False)) – 如果为 True，返回包含双重变量的字典。否则，仅返回最优运输成本。

  • return_matrix (boolean, 可选 (默认=False)) – 如果为真，则返回日志中的最佳运输矩阵。

  • center_dual (布尔值, 可选 (默认为True)) – 如果为True，使用函数 ot.lp.center_ot_dual()对双重潜力进行中心化。

  • numThreads (int 或 "max", 可选 (默认=1, 即不使用OpenMP)) – 如果使用OpenMP编译，则选择并行化的线程数。“max”选择可能的最高数量。

  • check_marginals (bool, optional (default=True)) – 如果为 True，将检查边际质量是否相等。如果为 False，跳过检查。

Returns:

  • W (float, array-like) – 给定参数的最优运输损失

  • log (dict) – 如果输入日志为真，则包含对偶变量和退出状态的字典

示例

简单的例子，显而易见的解决方案。函数 emd 接受列表并自动转换为 numpy 数组

>>> import ot
>>> a=[.5,.5]
>>> b=[.5,.5]
>>> M=[[0.,1.],[1.,0.]]
>>> ot.emd2(a,b,M)
0.0

参考文献

另请参见

ot.bregman.sinkhorn

熵正则化最优传输

ot.optim.cg

通用正则化OT

ot.lp.emd2_1d(x_a, x_b, a=None, b=None, metric='sqeuclidean', p=1.0, dense=True, log=False)[源]

解决一维测量之间的地球搬运工距离问题并返回损失

\[ \begin{align}\begin{aligned}\gamma = arg\min_\gamma \sum_i \sum_j \gamma_{ij} d(x_a[i], x_b[j])\\s.t. \gamma 1 = a, \gamma^T 1= b, \gamma\geq 0\end{aligned}\end{align} \]

其中 :

  • d 是该度量

  • x_a 和 x_b 是样本

  • a 和 b 是样本权重

该实现仅支持形式为 \(d(x, y) = |x - y|^p\) 的度量。

使用在 [1]_ 中详细描述的算法

Parameters:

  • x_a ((ns,) 或 (ns, 1) ndarray, float64) – 源 Dirac 位置（在实线上的位置）

  • x_b ((nt,) 或 (ns, 1) ndarray, float64) – 目标 Dirac 位置（在实数线上）

  • a ((ns,) ndarray, float64, 可选) – 源直方图（默认为均匀权重）

  • b ((nt,) ndarray, float64, 可选) – 目标直方图（默认为均匀权重）

  • 度量 (str, 可选 (默认='sqeuclidean')) – 要使用的度量。仅适用于字符串 ‘sqeuclidean’, ‘minkowski’, ‘cityblock’ 或 ‘euclidean’.

  • p (float, 可选 (默认为1.0)) – 如果 metric=’minkowski’，则应用的 p-norm

  • dense (boolean, optional (default=True)) – 如果为 True，则返回数学:gamma，以形状为 (ns, nt) 的稠密 ndarray 形式。否则返回使用 scipy 的 coo_matrix 格式的稀疏表示。仅在 log 设置为 True 时使用。由于实现细节，当将 dense 设置为 False 时，此函数运行得更快。

  • log (boolean, optional (default=False)) – 如果为True，返回一个包含运输矩阵的字典。否则仅返回损失。

Returns:

  • loss (float) – 与最优运输相关的成本

  • log (dict) – 如果输入日志为True，则包含给定参数的最优运输矩阵的字典

示例

简单的例子，解决方案明显。函数 emd2_1d 接受列表并执行自动转换为 numpy 数组

>>> import ot
>>> a=[.5, .5]
>>> b=[.5, .5]
>>> x_a = [2., 0.]
>>> x_b = [0., 3.]
>>> ot.emd2_1d(x_a, x_b, a, b)
0.5
>>> ot.emd2_1d(x_a, x_b)
0.5

参考文献

另请参见

ot.lp.emd2

多维分布的EMD

ot.lp.emd_1d

一维分布的EMD（返回运输矩阵而不是成本）

ot.lp.emd_1d(x_a, x_b, a=None, b=None, metric='sqeuclidean', p=1.0, dense=True, log=False, check_marginals=True)[源]

解决一维测量之间的地球搬运者距离问题并返回OT矩阵

\[ \begin{align}\begin{aligned}\gamma = arg\min_\gamma \sum_i \sum_j \gamma_{ij} d(x_a[i], x_b[j])\\s.t. \gamma 1 = a, \gamma^T 1= b, \gamma\geq 0\end{aligned}\end{align} \]

其中 :

  • d 是该度量

  • x_a 和 x_b 是样本

  • a 和 b 是样本权重

该实现仅支持形式为 \(d(x, y) = |x - y|^p\) 的度量。

使用在 [1]_ 中详细描述的算法

Parameters:

  • x_a ((ns,) 或 (ns, 1) ndarray, float64) – 源 Dirac 位置（在实线上的位置）

  • x_b ((nt,) 或 (ns, 1) ndarray, float64) – 目标 Dirac 位置（在实数线上）

  • a ((ns,) ndarray, float64, 可选) – 源直方图（默认为均匀权重）

  • b ((nt,) ndarray, float64, 可选) – 目标直方图（默认为均匀权重）

  • 度量 (str, 可选 (默认='sqeuclidean')) – 要使用的度量。仅适用于字符串 ‘sqeuclidean’, ‘minkowski’, ‘cityblock’ 或 ‘euclidean’.

  • p (float, 可选 (默认为1.0)) – 如果 metric=’minkowski’，则应用的 p-norm

  • dense (boolean, 可选 (默认=True)) – 如果为True，则返回形状为 (ns, nt) 的密集 ndarray，值为 math:gamma。否则返回使用 scipy 的 coo_matrix 格式的稀疏表示。由于实现细节，当使用 ‘sqeuclidean’、‘minkowski’、‘cityblock’ 或 ‘euclidean’ 距离度量时，此函数运行得更快。

  • log (布尔值, 可选 (默认=False)) – 如果为True，将返回一个包含成本的字典。否则仅返回最优运输矩阵。

  • check_marginals (bool, optional (default=True)) – 如果为 True，将检查边际质量是否相等。如果为 False，跳过检查。

Returns:

  • gamma ((ns, nt) ndarray) – 给定参数的最优运输矩阵

  • log (dict) – 如果输入的 log 为 True，则返回一个包含成本的字典

示例

简单的示例，显而易见的解决方案。函数 emd_1d 接受列表并进行自动转换为 numpy 数组

>>> import ot
>>> a=[.5, .5]
>>> b=[.5, .5]
>>> x_a = [2., 0.]
>>> x_b = [0., 3.]
>>> ot.emd_1d(x_a, x_b, a, b)
array([[0. , 0.5],
       [0.5, 0. ]])
>>> ot.emd_1d(x_a, x_b)
array([[0. , 0.5],
       [0.5, 0. ]])

参考文献

另请参见

ot.lp.emd

多维分布的EMD

ot.lp.emd2_1d

一维分布的EMD（返回成本而不是运输矩阵）

ot.lp.emd_1d_sorted(u_weights, v_weights, u, v, metric='sqeuclidean', p=1.0)

解决排序的一维测量之间的地球搬运工距离问题，并返回OT矩阵及相关成本

Parameters:

  • u_weights ((ns,) ndarray, float64) – 源直方图

  • v_weights ((nt,) ndarray, float64) – 目标直方图

  • u ((ns,) ndarray, float64) – 源dirac位置（在实线上）

  • v ((nt,) ndarray, float64) – 目标 Dirac 位置（在实数线上）

  • 度量 (str, 可选 (默认='sqeuclidean')) – 要使用的度量。仅适用于字符串 ‘sqeuclidean’, ‘minkowski’, ‘cityblock’ 或 ‘euclidean’.

  • p (float, 可选 (默认为1.0)) – 如果 metric=’minkowski’，则应用的 p-norm

Returns:

  • gamma ((n, ) ndarray, float64) – 最优运输矩阵中的值

  • indices ((n, 2) ndarray, int64) – 存储在gamma中的最优运输矩阵值的索引

  • cost – 与最优运输相关的费用

ot.lp.free_support_barycenter(measures_locations, measures_weights, X_init, b=None, weights=None, numItermax=100, stopThr=1e-07, verbose=False, log=None, numThreads=1)[源]

解决自由支撑（重心的位置被优化，而不是权重）Wasserstein 重心问题（即 2-Wasserstein 距离的加权 Frechet 均值），正式定义为：

\[\min_\mathbf{X} \quad \sum_{i=1}^N w_i W_2^2(\mathbf{b}, \mathbf{X}, \mathbf{a}_i, \mathbf{X}_i)\]

其中 :

  • \(w \in \mathbb{(0, 1)}^{N}\) 是 barycenter 权重，其总和为 1

  • measure_weights 表示 \(\mathbf{a}_i \in \mathbb{R}^{k_i}\): 经验度量权重（在单纯形上）

  • measures_locations 指的是 \(\mathbf{X}_i \in \mathbb{R}^{k_i, d}\): 经验测量原子的位置

  • \(\mathbf{b} \in \mathbb{R}^{k}\) 是所需的重心权重向量

这个问题在[20]（算法 2）中被考虑。以下代码有两个不同之处：

  • 我们不对权重进行优化

  • 我们不进行位置更新的线搜索，我们使用即 \(\theta = 1\) 在 [20]（算法 2）中。这可以看作是在连续设置中 [43] 提出的固定点算法的离散实现。

Parameters:

  • measures_locations (列表 的 N (k_i,d) 数组类型) – 测量支持于 \(k_i\) 位置的离散支持，在一个 d 维空间中 (\(k_i\) 对于列表的每个元素可以是不同的)

  • measures_weights (列表 的 N (k_i,) 类数组) – Numpy 数组，其中每个 numpy 数组具有 \(k_i\) 个非负值，总和为一，代表每个离散输入度量的权重

  • X_init ((k,d) 数组类型) – 重心的支持位置（在 k 个原子上）的初始化

  • b ((k,) 类似数组) – 重心权重的初始化（非负数，总和为1）

  • 权重 ((N,) 类数组) – 重心系数的初始化（非负，和为1）

  • numItermax (int, 可选) – 最大迭代次数

  • stopThr (float, 可选) – 错误的停止阈值 (>0)

  • verbose (bool, 可选) – 在迭代过程中打印信息

  • log (bool, 可选) – 如果为真，则记录日志

  • numThreads (int 或 "max", 可选 (默认=1, 即不使用OpenMP)) – 如果使用OpenMP编译，则选择并行化的线程数。“max”选择可能的最高数量。

Returns:

X – 重心的支持位置（在k个原子上）

Return type:

(k,d) 类似数组

参考文献

ot.lp.generalized_free_support_barycenter(X_list, a_list, P_list, n_samples_bary, Y_init=None, b=None, weights=None, numItermax=100, stopThr=1e-07, verbose=False, log=None, numThreads=1, eps=0)[源]

解决自由支持广义沃瑟斯坦重心问题：寻找一个重心（一个具有固定数量均匀权重的离散测度），其相应的投影符合输入测度。更正式地说：

\[\min_\gamma \quad \sum_{i=1}^p w_i W_2^2(\nu_i, \mathbf{P}_i\#\gamma)\]

其中 :

  • \(\gamma = \sum_{l=1}^n b_l\delta_{y_l}\) 是期望的重心，其中每个 \(y_l \in \mathbb{R}^d\)

  • \(\mathbf{b} \in \mathbb{R}^{n}\) 是重心所需的权重向量

  • 输入度量为 \(\nu_i = \sum_{j=1}^{k_i}a_{i,j}\delta_{x_{i,j}}\)

  • 各个\(\mathbf{a}_i \in \mathbb{R}^{k_i}\) 是相应的经验测量权重（在简单形上）

  • 每个\(\mathbf{X}_i \in \mathbb{R}^{k_i, d_i}\)是各自经验度量原子的位置

  • \(w = (w_1, \cdots w_p)\) 是重心系数（在单纯形上）

  • 每个 \(\mathbf{P}_i \in \mathbb{R}^{d, d_i}\)，并且 \(P_i\#\nu_i = \sum_{j=1}^{k_i}a_{i,j}\delta_{P_ix_{i,j}}\)

正如[42]所示，这个问题可以被重写为Wasserstein Barycenter问题，我们使用自由支撑方法[20]（算法2）来解决。

Parameters:

  • X_list (列表 of p (k_i,d_i) 类数组) – 输入测量的离散支持：每个支持包含\(k_i\)个位置，位于一个d_i维空间中 (\(k_i\)可以对列表中的每个元素不同)

  • a_list (列表 的 p (k_i,) 数组类似) – 测量权重：每个元素是单纯形上的一个向量 (k_i)

  • P_list (列表 of p (d_i,d) 数组类似) – 每个 \(P_i\) 是一个线性映射 \(\mathbb{R}^{d} \rightarrow \mathbb{R}^{d_i}\)

  • n_samples_bary (int) – 重心点的数量

  • Y_init ((n_samples_bary,d) array-like) – 重心的支持位置初始化（在 k 原子上）

  • b ((n_samples_bary,) array-like) – 重心测量的权重初始化（在简单形体上）

  • weights ((p,) array-like) – 重心系数的初始化（在单纯形上）

  • numItermax (int, 可选) – 最大迭代次数

  • stopThr (float, 可选) – 错误的停止阈值 (>0)

  • verbose (bool, 可选) – 在迭代过程中打印信息

  • log (bool, 可选) – 如果为真，则记录日志

  • numThreads (int 或 "max", 可选 (默认=1, 即不使用OpenMP)) – 如果使用OpenMP编译，则选择并行化的线程数。“max”选择可能的最高数量。

  • eps (变量矩阵反演的稳定性系数 ) – 如果 \(\mathbf{P}_i^T\) 矩阵无法生成 \(\mathbb{R}^d\)，则该问题是未定义的，矩阵反演将失败。在这种情况下，可以设置 eps=1e-8 并仍然得到一个解（这可能意义不大）

Returns:

Y – 重心的支持位置（在 n_samples_bary 原子上）

Return type:

(n_samples_bary,d) 类数组

参考文献

ot.lp.semidiscrete_wasserstein2_unif_circle(u_values, u_weights=None)[源]

计算样本与均匀分布之间的闭式形式的2-Wasserstein距离，位于 \(S^1\) 样本需要在 \(S^1\cong [0,1[\)。如果它们在 \(\mathbb{R}\) 中， 则取模1的值。 如果值位于 \(S^1\subset\mathbb{R}^2\)，则需要首先使用例如 atan2 函数找到坐标。

\[W_2^2(\mu_n, \nu) = \sum_{i=1}^n \alpha_i x_i^2 - \left(\sum_{i=1}^n \alpha_i x_i\right)^2 + \sum_{i=1}^n \alpha_i x_i \left(1-\alpha_i-2\sum_{k=1}^{i-1}\alpha_k\right) + \frac{1}{12}\]

其中：

  • \(\nu=\mathrm{Unif}(S^1)\) 和 \(\mu_n = \sum_{i=1}^n \alpha_i \delta_{x_i}\)

对于值 \(x=(x_1,x_2)\in S^1\)，需要首先获取它们的坐标，方法是

\[u = \frac{\pi + \mathrm{atan2}(-x_2,-x_1)}{2\pi},\]

使用例如 ot.utils.get_coordinate_circle(x)

Parameters:

  • u_values (ndarray, shape (n, ...)) – 样本

  • u_weights (ndarray, shape (n, ...), optional) – 源领域中的样本权重

Returns:

loss – 与最佳运输相关的成本

Return type:

float

示例

>>> x0 = np.array([[0], [0.2], [0.4]])
>>> semidiscrete_wasserstein2_unif_circle(x0)
array([0.02111111])

参考文献

ot.lp.wasserstein_1d(u_values, v_values, u_weights=None, v_weights=None, p=1, require_sort=True)[源]

计算两个（批处理的）经验分布之间的1维OT损失[15]

它正式地是p-Wasserstein距离的p次方。我们通过首先构建各个分位数函数，然后对它们进行积分，以向量化的方式进行。

当后端与numpy不同，并且需要对样本位置或权重进行梯度计算时，应优先使用此函数而不是 emd_1d。

Parameters:

  • u_values (数组类型, 形状 (n, ...)) – 第一个经验分布的位置

  • v_values (类数组, 形状 (m, ...)) – 第二个经验分布的位置

  • u_weights (类似数组, 形状 (n, ...), 可选) – 第一组经验分布的权重，如果为 None，则使用均匀权重

  • v_weights (array-like, 形状 (m, ...), 可选) – 第二个经验分布的权重，如果为 None 则使用均匀权重

  • p (int, 可选) – 使用的基础度量的阶数，应该至少为 1（见 [2, 第 2 章]，默认为 1

  • require_sort (bool, optional) – 对分布原子的位置信息进行排序，如果为 False，我们将认为它们在传递给函数之前已经被排序，默认值为 True

Returns:

cost – 批量化的EMD

Return type:

浮点数/类似数组，形状 (…)

参考文献

ot.lp.wasserstein_circle(u_values, v_values, u_weights=None, v_weights=None, p=1, Lm=10, Lp=10, tm=-1, tp=1, eps=1e-06, require_sort=True)[源]

使用[45]计算圆上的Wasserstein距离，当p=1时使用，其他情况下使用[44]提出的二分查找算法。样本需要在\(S^1\cong [0,1[\)中。如果它们在\(\mathbb{R}\)上，则取模1的值。如果值在\(S^1\subset\mathbb{R}^2\)上，则需要首先使用例如atan2函数找到坐标。

返回的总损失：

\[OT_{loss} = \inf_{\theta\in\mathbb{R}}\int_0^1 |cdf_u^{-1}(q) - (cdf_v-\theta)^{-1}(q)|^p\ \mathrm{d}q\]

对于 p=1, [45]

\[W_1(u,v) = \int_0^1 |F_u(t)-F_v(t)-LevMed(F_u-F_v)|\ \mathrm{d}t\]

对于值 \(x=(x_1,x_2)\in S^1\)，需要首先获取它们的坐标，方法是

\[u = \frac{\pi + \mathrm{atan2}(-x_2,-x_1)}{2\pi}\]

使用例如 ot.utils.get_coordinate_circle(x)

该函数在后台运行，但不支持tensorflow和jax。

Parameters:

  • u_values (ndarray, shape (n, ...)) – 源域中的样本（坐标在 [0,1[）

  • v_values (ndarray, shape (n, ...)) – 目标领域中的样本（坐标在 [0,1[ 上）

  • u_weights (ndarray, shape (n, ...), optional) – 源领域中的样本权重

  • v_weights (ndarray, shape (n, ...), 可选) – 目标域中的样本权重

  • p (float, 可选 (默认=1)) – 用于计算Wasserstein距离的功率p

  • Lm (int, 可选) – 下界 dC。对于 p>1。

  • Lp (int, 可选) – 上限 dC。对于 p>1。

  • tm (float, 可选) – 下界theta。对于 p>1。

  • tp (float, 可选) – 上界 theta。对于 p>1。

  • eps (float, 可选) – 停止条件。对于 p>1。

  • require_sort (bool, 可选) – 如果为 True，则对值进行排序。

Returns:

loss – 与最佳运输相关的成本

Return type:

float

示例

>>> u = np.array([[0.2,0.5,0.8]])%1
>>> v = np.array([[0.4,0.5,0.7]])%1
>>> wasserstein_circle(u.T, v.T)
array([0.1])

参考文献