statsmodels.tsa.seasonal.MSTL¶

class statsmodels.tsa.seasonal.MSTL(endog, periods=None, windows=None, lmbda=None, iterate=2, stl_kwargs=None)[source]¶

使用LOESS进行多季节性的季节趋势分解。

在版本0.14.0中添加。

Parameters:¶

endogarray_like

要分解的数据。必须可以压缩到1维。

periods{int, array_like, None}, optional

季节成分的周期性。如果为None且endog是pandas Series或DataFrame，则尝试从endog中确定。如果endog是ndarray，则必须提供周期。

windows{int, array_like, None}, optional

每个对应周期的季节平滑器的长度。 必须是奇数整数，通常应大于等于7（默认）。如果为None，则使用默认值，该值由7 + 4 * np.arange(1, n + 1, 1)确定，其中n是季节成分的数量。

lmbda{float, str, None}, optional

应用于endog的Box-Cox变换的lambda参数，在分解之前。如果为None，则不应用变换。如果为“auto”，将估计一个值，该值最大化对数似然函数。

iterateint, optional

用于细化季节性成分的迭代次数。

stl_kwargs: dict, optional

传递给STL的参数。

另请参阅

statsmodels.tsa.seasonal.STL

参考文献

[1]

K. Bandura, R.J. Hyndman, 和 C. Bergmeir (2021) MSTL: 一种用于具有多季节模式的时间序列的季节性趋势分解算法。arXiv 预印本 arXiv:2107.13462。

示例

首先创建一个具有每小时频率和多个季节性成分的玩具数据集。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> import pandas as pd
>>> pd.plotting.register_matplotlib_converters()
>>> np.random.seed(0)
>>> t = np.arange(1, 1000)
>>> trend = 0.0001 * t ** 2 + 100
>>> daily_seasonality = 5 * np.sin(2 * np.pi * t / 24)
>>> weekly_seasonality = 10 * np.sin(2 * np.pi * t / (24 * 7))
>>> noise = np.random.randn(len(t))
>>> y = trend + daily_seasonality + weekly_seasonality + noise
>>> index = pd.date_range(start='2000-01-01', periods=len(t), freq='h')
>>> data = pd.DataFrame(data=y, index=index)

使用MSTL将时间序列分解为两个季节性成分，周期分别为24（每日季节性）和24*7（每周季节性）。

>>> from statsmodels.tsa.seasonal import MSTL
>>> res = MSTL(data, periods=(24, 24*7)).fit()
>>> res.plot()
>>> plt.tight_layout()
>>> plt.show()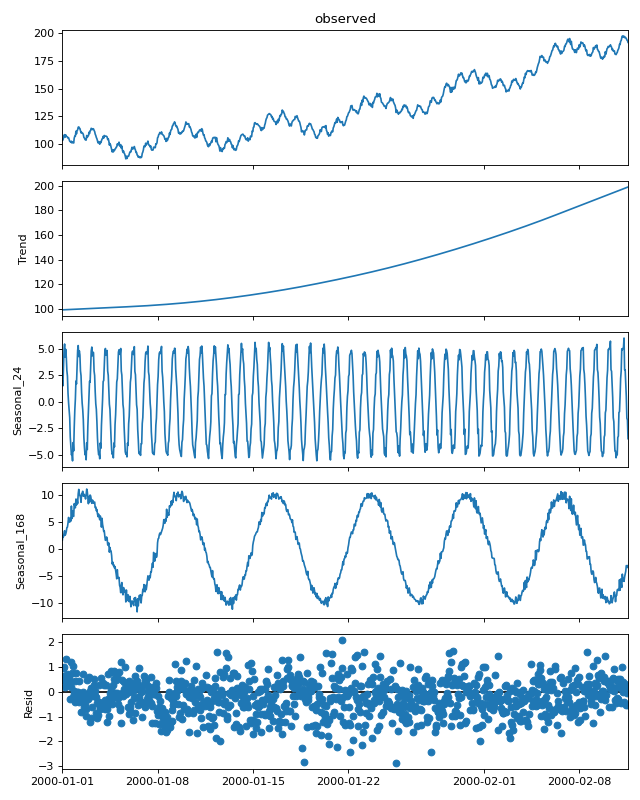

(源代码, png, 高分辨率png, pdf)

方法

fit()

估计一个趋势分量、多个季节性分量和一个残差分量。