相关工作¶

乍看之下，Triton可能只是又一个用于深度神经网络的领域特定语言。本节的目的是将Triton置于语境中，并强调其与该领域两种主流方法——多面体编译和调度语言——的区别。

多面体编译¶

传统编译器通常依赖中间表示形式，如LLVM-IR [LATTNER2004]，这些表示使用(非)条件分支编码控制流信息。这种相对低级的格式使得静态分析输入程序的运行时行为(例如缓存未命中)变得困难，也难以通过使用分块[WOLFE1989]、融合[DARTE1999]和交换[ALLEN1984]等技术自动优化循环。为解决这个问题，多面体编译器[ANCOURT1991]依赖具有静态可预测控制流的程序表示，从而能够针对数据局部性和并行性进行激进的编译时程序转换。尽管这一策略已被许多面向DNN的语言和编译器采用，如Tiramisu[BAGHDADI2021]、Tensor Comprehensions[VASILACHE2018]、Diesel[ELANGO2018]以及MLIR中的Affine方言[LATTNER2019]，但它也存在一些局限性，这些将在本节后面描述。

程序表示¶

多面体编译是一个广阔的研究领域。在本节中，我们仅概述该主题的最基本方面，但对底层坚实数学基础感兴趣的读者可以参考关于线性和整数规划的丰富文献。

for(int i = 0; i < 3; i++)
for(int j = i; j < 5; j++)
  A[i][j] = 0;

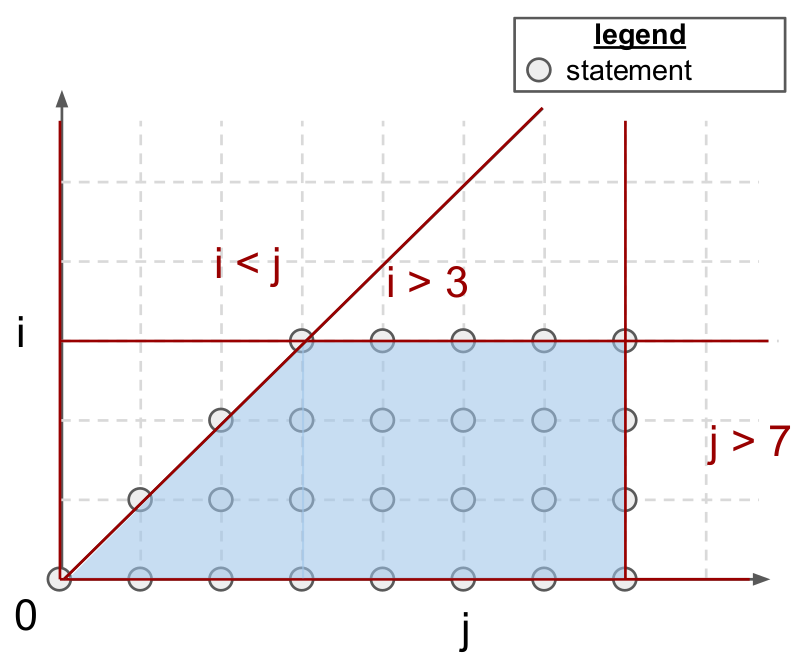
多面体编译器专注于一类通常被称为静态控制部分(SCoP)的程序，即连续语句的最大集合，其中条件语句和循环边界是周围循环索引和全局不变参数的仿射函数。如上所示，这种格式的程序总是导致迭代域受仿射不等式(即多面体)的限制。这些多面体也可以用代数方式定义；对于上述示例：

\[\begin{split}\mathcal{P} = \{ i, j \in \mathbb{Z}^2 ~|~ \begin{pmatrix} 1 & 0 \\ -1 & 0 \\ -1 & 1 \\ 0 & -1 \\ \end{pmatrix} \begin{pmatrix} i \\ j \end{pmatrix} + \begin{pmatrix} 0 \\ 2 \\ 0 \\ 4 \end{pmatrix} \geq 0 \}\end{split}\]

集合\(\mathcal{P}\)中的每个点\((i, j)\)代表一个多面体语句，即满足以下条件的程序语句：(1) 不会引发控制流副作用（例如for、if、break）；(2) 数组访问中仅包含循环索引和全局参数的仿射函数。为了便于别名分析，数组访问还会通过所谓的访问函数进行数学抽象。换句话说，A[i][j]本质上就是A[f(i,j)]，其中访问函数\(f\)定义为：

\[\begin{split}f(i, j) = \begin{pmatrix} 1 & 0\\ 0 & 1\\ \end{pmatrix} \begin{pmatrix} i\\ j \end{pmatrix} = (i, j)\end{split}\]

请注意，SCoP的迭代域并不指定其语句的执行顺序。实际上，这个迭代域可以通过许多不同的合法顺序（即调度）来遍历。从形式上看，调度被定义为循环索引\(\mathbf{x}\)和全局不变参数\(\mathbf{g}\)的一个p维仿射变换\(\Theta\)：

\[\begin{split}\Theta_S(\mathbf{x}) = T_S \begin{pmatrix} \vec{x}\\ \vec{g}\\ 1 \end{pmatrix} \qquad T_S \in \mathbb{Z} ^{p \times (\text{dim}(\mathbf{x}) + \text{dim}(\mathbf{g}) + 1)}\end{split}\]

其中\(\Theta_S(\mathbf{x})\)是一个p维向量，表示在遍历环绕\(S\)的循环嵌套时从最慢增长到最快增长的索引（从左到右）。对于上面显示的代码，可以通过以下方式检索由C语言中循环嵌套定义的原始调度：

\[\begin{split}\Theta_S(\mathbf{x}) = \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ \end{pmatrix} \begin{pmatrix} i & j \end{pmatrix}^T = \begin{pmatrix} i & j \end{pmatrix}^T\end{split}\]

其中\(i\)和\(j\)分别是循环嵌套中增长最慢和最快的索引。如果\(T_S\)是一个向量(或张量)，那么\(\Theta_S\)被称为一维(或多维)的。

优势¶

适合多面体编译的程序可以进行激进的转换和优化。这些转换中的大多数实际上归结为生成调度和迭代域，从而实现促进并行性和空间/时间数据局部性的循环转换（例如融合、交换、分块、并行化）。

多面体编译器还可以自动执行复杂的验证过程，以确保其输入程序的语义在整个优化阶段得到保留。需要注意的是，多面体优化器与更标准的优化技术并不冲突。事实上，这些系统通常被实现为一组LLVM pass，可以在更传统的编译技术之前运行[GROSSER2012]。

总而言之，多面体机制在适用场景下极其强大。它已被证明能够支持大多数常见的循环变换，并且确实在密集矩阵乘法等任务上实现了与最先进GPU库相媲美的性能[ELANGO2018]。此外，该机制完全自动化，除了需要类似C语言的源代码外，不需要程序员提供任何额外提示。

限制¶

遗憾的是，多面体编译器存在两个主要限制，阻碍了其作为神经网络代码生成的通用方法被广泛采用。

首先，可能的程序转换集合\(\Omega = \{ \Theta_S ~|~ S \in \text{program} \}\)非常庞大，并且随着程序中语句数量的增加以及其迭代域大小的增长而扩大。验证每个转换的合法性可能还需要解决复杂的整数线性规划问题，这使得多面体编译在计算上非常昂贵。更糟糕的是，硬件属性（例如缓存大小、SM数量）和上下文特征（例如输入张量形状）也必须由该框架考虑在内，从而导致昂贵的自动调优过程[SATO2019]。

其次，多面体框架的通用性不强；SCoPs相对常见[GIRBAL2006]，但要求循环边界和数组下标必须是循环索引的仿射函数，这通常只出现在规则密集的计算中。因此，该框架尚未成功应用于稀疏或甚至结构化稀疏的神经网络，而这些网络在过去几年中的重要性迅速上升。

另一方面，本论文所倡导的块状程序表示法在范围上限制较少，并且可以通过标准数据流分析实现接近峰值性能。

调度语言¶

关注点分离 [DIJKSTRA82] 是计算机科学中一个众所周知的设计原则：程序应该被分解成模块化的抽象层，将算法的语义与其实现细节分离开来。像Halide和TVM这样的系统将这一理念更进一步，通过使用调度语言在语法层面强制执行这种分离。这种方法的好处在矩阵乘法的情况下尤为明显，如下所示，算法的定义（第1-7行）与其实现（第8-16行）完全分离，这意味着两者可以独立维护、优化和分发。

// algorithm
Var x("x"), y("y");
Func matmul("matmul");
RDom k(0, matrix_size);
RVar ki;
matmul(x, y) = 0.0f;
matmul(x, y) += A(k, y) * B(x, k);
// schedule
Var xi("xi"), xo("xo"), yo("yo"), yi("yo"), yii("yii"), xii("xii");
matmul.vectorize(x, 8);
matmul.update(0)
    .split(x, x, xi, block_size).split(xi, xi, xii, 8)
    .split(y, y, yi, block_size).split(yi, yi, yii, 4)
    .split(k, k, ki, block_size)
    .reorder(xii, yii, xi, ki, yi, k, x, y)
    .parallel(y).vectorize(xii).unroll(xi).unroll(yii);

然而，生成的代码可能不完全具备可移植性，因为调度方案有时依赖于并非广泛可用的执行模型（例如SPMD）或硬件内置功能（例如矩阵乘积累加）。这个问题可以通过自动调度机制[MULLAPUDI2016]来缓解。

优势¶

这种方法的主要优势是它允许程序员只需编写一次算法，而将性能优化作为单独的任务来处理。这使得可以手动指定那些多面体编译器无法通过静态数据流分析自动找出的优化方案。

调度语言无疑是神经网络代码生成中最流行的方法之一。用于此目的的最流行系统可能是TVM，它在各种平台上提供良好的性能以及内置的自动调度机制。

限制¶

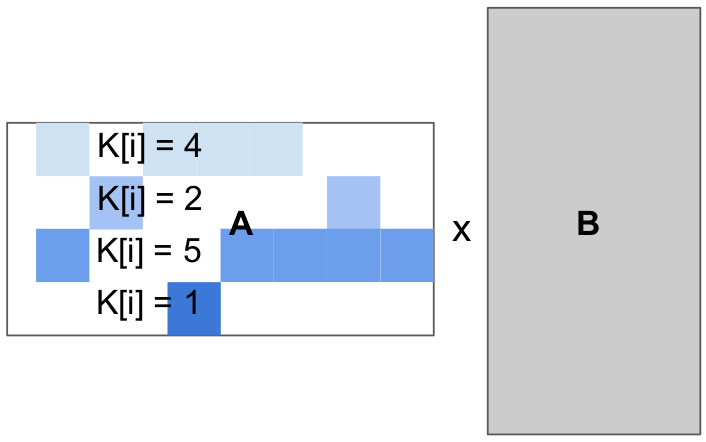
这种开发便捷性是有代价的。首先，在适用情况下（例如使用相同分块大小的V100/A100张量核心时），遵循这种范式的现有系统通常明显比Triton慢。我确实认为这不是调度语言的根本问题——从某种意义上说，通过更多努力可能可以解决——但这可能意味着这些系统更难设计。更重要的是，现有调度语言生成的循环边界和增量无法依赖外围循环索引，至少会对可能的调度方案施加严重限制——甚至可能导致系统完全失效。这对于稀疏计算来说是个问题，因为其迭代空间可能是不规则的。

for(int i = 0; i < 4; i++)
for(int j = 0; j < 4; j++)
  float acc = 0;
  for(int k = 0; k < K[i]; k++)
    acc += A[i][col[i, k]] * B[k][j]
  C[i][j] = acc;