GraphBLAS 入门指南

本入门指南涵盖：

• 什么是图？

• 存储图的常见方法

• 使用线性代数的Pagerank

• 半环简介

• SSSP 在 python-graphblas 中

• 摘要

什么是图？

图是由一组节点（也称为顶点）通过边连接而成的。

当边具有关联的方向（即箭头）时，图是有向的。

下图是一个任务图，意味着后续任务只有在所有先前的依赖项完成后才能开始。

当边没有定义方向时，图是无向的。

在以下社交网络中，假设友谊是相互的，因此在表示友谊作为边时，方向是不必要的。

请注意，图并不是完全连接的。图中所有节点并不需要从任何其他节点可达。

边可以有关联的权重。权重的含义取决于图的性质。对于道路网络，它可能表示基于道路长度和公布的速度限制的旅行时间。

此图展示了图中可能出现的复杂性。自环边的起点和终点是同一个节点。

存储图的常见方法

存储图的最常见方式是作为边列表，包含(start_node, end_node, weight)。

下面的图表及其边列表如下所示。

(0, 1, 5.6)
(0, 2, 2.3)
(0, 3, 4.6)
(1, 2, 1.9)
(1, 3, 6.2)
(2, 3, 3.0)
(3, 4, 1.4)
(4, 5, 4.4)
(4, 6, 1.0)
(5, 6, 2.8)

请注意，每条边只列出一次。边列表需要指明这些边是有向边还是无向边。

虽然边列表易于创建，但它们在性能上并不理想。查找连接到节点3的所有边需要对列表进行完整扫描。因此，存在其他格式可以使常见操作更加高效。

例如，networkx 使用字典的字典来存储图，这样可以方便地查询每个节点的出边。在无向图的情况下，这需要双倍的内存使用，但可以使图算法运行得更快。

# networkx-style storage of an undirected graph
G = {
    0: {1: {"weight": 5.6}, 2: {"weight": 2.3}, 3: {"weight": 4.6}},
    1: {0: {"weight": 5.6}, 2: {"weight": 1.9}, 3: {"weight": 6.2}},
    2: {0: {"weight": 2.3}, 1: {"weight": 1.9}, 3: {"weight": 3.0}},
    3: {0: {"weight": 4.6}, 1: {"weight": 6.2}, 2: {"weight": 3.0}, 4: {"weight": 1.4}},
    4: {3: {"weight": 1.4}, 5: {"weight": 4.4}, 6: {"weight": 1.0}},
    5: {4: {"weight": 4.4}, 6: {"weight": 2.8}},
    6: {4: {"weight": 1.0}, 5: {"weight": 2.8}},
}

存储图的另一种方式是作为邻接矩阵。每个节点在矩阵中既是一行也是一列。矩阵中的单元格填充了边的权重（如果存在）。这自然形成了一个稀疏的方阵。

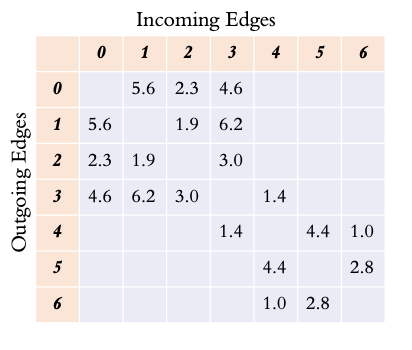
沿着行读取时，显示的是出边，而沿着列读取时，显示的是节点的入边。

在无向图的情况下，图是对称的，因此对于这个例子，属性可能不明显。

虽然邻接矩阵在概念上是一种很好的工作格式，但将完整矩阵存储为二维密集数组会非常低效。相反，存在一些格式可以有效地仅存储存在的值。

存在多种格式用于高效地仅存储当前值。示例包括压缩稀疏行（CSR）以及超稀疏CSR格式（也称为双压缩稀疏行）。这些格式在按行迭代稀疏矩阵时非常有效。也存在类似的面向列的格式。

使用线性代数的Pagerank

一旦我们进入使用稀疏矩阵存储图的领域，自然的问题是线性代数领域是否可以用来对图表示做任何有用的事情。

让我们来看一个关于Pagerank的激励性例子，这是网络搜索领域中最著名的图分析指标之一。

Pagerank 获取给定节点的权重，并以迭代方式将其分配给每个连接的节点，直到过程收敛。每个节点的最终值是 pagerank，通常表示该节点在整个图中的重要性。

这是networkx pagerank算法的简化版本。最外层的for循环用于算法的整体收敛。两个内层的for循环遍历每个节点的每条边。由于Python处理for循环的方式，这相当慢。

for _ in range(max_iter):
    xlast = x
    x = dict.fromkeys(xlast.keys(), 0)
    for n in x:
        for _, nbr, wt in W.edges(n, data=weight):
            x[nbr] += alpha * xlast[n] * wt
    # check convergence, l1 norm
    err = sum(abs(x[n] - xlast[n]) for n in x)
    if err < N * tol:
        return x
raise nx.PowerIterationFailedConvergence(max_iter)

Pagerank 使用线性代数有一个非常自然的表示。内部的 for 循环只是简单地执行矩阵与向量的乘法。

这是使用scipy.sparse矩阵和向量的相同算法。它既更易于阅读，也更快，因为矩阵乘法可以分派给scipy。

for _ in range(max_iter):
    xlast = x
    x = alpha * (x @ A)
    # check convergence, l1 norm
    err = np.absolute(x - xlast).sum()
    if err < N * tol:
        return dict(zip(nodelist, map(float, x)))
raise nx.PowerIterationFailedConvergence(max_iter)

半环简介

使用稀疏向量表示每个节点的当前值，并使用稀疏邻接矩阵表示图的边，向量-矩阵乘法相当于执行广度优先搜索（BFS）的一步。

每个节点的值乘以每条边的权重，然后这些新值由接收节点相加。通过这种方式，初始节点的值首先传播到一跳邻居，然后传播到两跳邻居，依此类推。

这种将值传播给邻居的想法是许多图算法的基础。然而，与使用标准的矩阵乘法运算符（将元素相乘并相加结果）不同，其他运算符以相同的方式使用。这些被称为半环。

执行矩阵乘法的“标准”方法是使用plus_times半环。

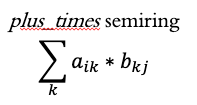
另一种半环是min_plus半环。

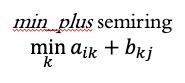
从概念上讲，min_plus 半环取一个节点的值，将其加到边的权重上，并在接收节点收集值时，取最小的值。

为什么这有用？

因为使用min_plus半环进行重复的BFS将使用线性代数计算单源最短路径（SSSP）算法。

在python-graphblas中的SSSP

以下是用于计算从节点0开始的单源最短路径的python-graphblas算法。

from graphblas import op, semiring, Matrix, Vector

# Create the graph and starting vector
start_node = 0
G = Matrix.from_coo(
    [0, 0, 1, 1, 2],
    [1, 2, 2, 3, 3],
    [2.0, 5.0, 1.5, 4.25, 0.5],
    nrows=4,
    ncols=4
)
v = Vector.from_coo([start_node], [0.0], size=4)

# Compute SSSP
while True:
    w = v.dup()

    # Perform a BFS step using min_plus semiring
    # Accumulate into v using the `min` function
    v(op.min) << semiring.min_plus(v @ G)

    # The algorithm is converged once v stops changing
    if v.isequal(w):
        break

结果发现从节点0到节点3的最短路径长度为4.0，该路径经过节点1和节点2。虽然这不是最直接的路径，但它是最短的。

存在其他算法用于在回溯到源节点时识别每个节点的父节点，但此算法仅计算最短路径长度。

摘要

本入门教程简要介绍了图，将图表示为稀疏邻接矩阵，并展示了线性代数可以通过扩展半环的概念来计算图算法。

这是一个相对较新的研究领域，因此每年都有许多学术论文和演讲发表。 Graphblas.org 仍然是了解该领域最新发展的最佳来源。

许多人将从用GraphBLAS编写的更快图算法中受益，但对于那些想要探索GraphBLAS全部功能的人来说，亲自动手编写代码是无可替代的。阅读用户指南以了解更多信息。