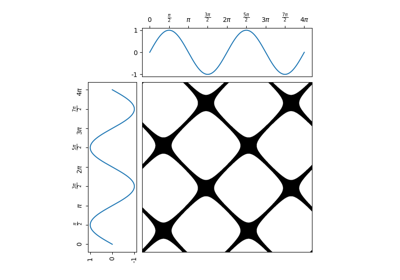
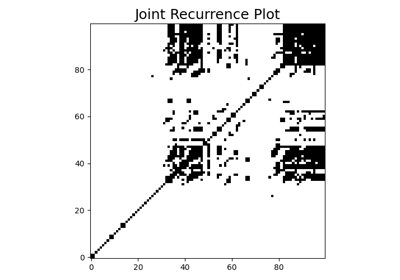
pyts.image.递归图

class pyts.image.RecurrencePlot(dimension=1, time_delay=1, threshold=None, percentage=10, flatten=False)[来源]

递归图。

递归图是一种图像，用于表示从原始时间序列中提取的轨迹之间的距离。

Parameters:
dimension : int or float (default = 1)

轨迹的维度。如果是浮点数，它表示每个时间序列大小的百分比，必须在0到1之间。

time_delay : int or float (default = 1)

轨迹中两个连续点之间的时间间隔。如果是浮点数，它表示每个时间序列大小的百分比，必须在0到1之间。

threshold : float, ‘point’, ‘distance’ or None (default = None)

最小距离的阈值。如果为None，则递归图不会被二值化。如果为'point'，则计算阈值使得percentage百分比的点小于该阈值。如果为'distance'，则计算阈值作为最大距离的percentage百分比。

percentage : int or float (default = 10)

如果threshold='point'则为黑点的百分比，如果threshold='distance'则为最大距离的百分比阈值。 如果threshold是浮点数或None则忽略。

flatten : bool (default = False)

如果为True，图像将被展平为一维。

注意事项

给定一个时间序列 (x_1, \ldots, x_n)，提取的轨迹是

\vec{x}_i = (x_i, x_{i + \tau}, \ldots, x_{i + (m - 1)\tau}), \quad \forall i \in \{1, \ldots, n - (m - 1)\tau \}

其中 R 是轨迹的 dimension 维度，R 是 time_delay 时间延迟。递归图（记作 R）表示轨迹之间的成对距离

R_{i, j} = \Theta(\varepsilon - \| \vec{x}_i - \vec{x}_j \|), \quad \forall i,j \in \{1, \ldots, n - (m - 1)\tau \}

其中 \varepsilon 是赫维赛德函数，\varepsilon 是 threshold。

参考文献

[1]J.-P Eckmann, S. Oliffson Kamphorst 和 D Ruelle，《动力系统的递归图》。欧洲物理快报（1987）。

示例

>>> from pyts.datasets import load_gunpoint
>>> from pyts.image import RecurrencePlot
>>> X, _, _, _ = load_gunpoint(return_X_y=True)
>>> transformer = RecurrencePlot()
>>> X_new = transformer.transform(X)
>>> X_new.shape
(50, 150, 150)

方法

__init__([dimension, time_delay, threshold, …]) Initialize self.
fit([X, y]) Pass.
fit_transform(X[, y]) Fit to data, then transform it.
get_params([deep]) Get parameters for this estimator.
set_params(**params) Set the parameters of this estimator.
transform(X) Transform each time series into a recurrence plot.
__init__(dimension=1, time_delay=1, threshold=None, percentage=10, flatten=False)[来源]

初始化自身。查看 help(type(self)) 获取准确的签名信息。

fit(X=None, y=None)[来源]

通过。

参数:
X

忽略

y

忽略
返回值:
self : object
fit_transform(X, y=None, **fit_params)

拟合数据，然后进行转换。

使用可选参数fit_params将转换器适配到X和y，并返回转换后的X版本。

参数:
X : array-like, shape = (n_samples, n_timestamps)

单变量时间序列。

y : None or array-like, shape = (n_samples,) (default = None)

目标值(无监督转换时为None)。

**fit_params : dict

额外的拟合参数。
返回值:
X_new : array

转换后的数组。
get_params(deep=True)

获取此估计器的参数。

参数：
deep : bool, default=True

如果为True，将返回此估计器及其包含的子估计器的参数。
返回值:
params : dict

参数名称映射到对应的值。
set_params(**params)

设置此估计器的参数。

该方法不仅适用于简单的估计器，也适用于嵌套对象（如Pipeline）。后者采用<component>__<parameter>形式的参数，从而可以更新嵌套对象的每个组件。

参数:
**params : dict

估计器参数。
返回值:
self : 估计器实例

估计器实例。
transform(X)[来源]

将每个时间序列转换为递归图。

参数:
X : 类数组, 形状 = (n_samples, n_timestamps)
Returns:
X_new : array, shape = (n_samples, image_size, image_size)

递归图。image_size表示轨迹数量，等于n_timestamps - (dimension - 1) * time_delay。如果flatten=True，则形状为(n_samples, image_size * image_size)。

使用pyts.image.RecurrencePlot的示例

Data set of recurrence plots

递归图数据集

递归图数据集
Single recurrence plot

单一递归图

单一递归图
Joint Recurrence Plot

联合递归图

联合递归图