绘图¶

介绍¶

绘图模块允许您制作二维和三维图表。目前，图表使用 matplotlib 作为后端进行渲染。如果没有 matplotlib，也可以使用 TextBackend 绘制二维图表。

绘图模块具有以下功能：

plot(): 绘制二维线条图。
plot_parametric(): 绘制二维参数图。
plot_implicit(): 绘制二维隐函数和区域图。
plot3d(): 绘制两个变量函数的3D图。
plot3d_parametric_line(): 绘制由参数定义的3D线条图。
plot3d_parametric_surface(): 绘制三维参数曲面图。

上述功能仅用于方便和易用。可以通过将相应的 Series 类作为参数传递给 Plot 来绘制任何图表。

绘图类¶

class sympy.plotting.plot.Plot(

*args,

title=None,

xlabel=None,

ylabel=None,

zlabel=None,

aspect_ratio='auto',

xlim=None,

ylim=None,

axis_center='auto',

axis=True,

xscale='linear',

yscale='linear',

legend=False,

autoscale=True,

margin=0,

annotations=None,

markers=None,

rectangles=None,

fill=None,

backend='default',

size=None,

**kwargs,

)[源代码][源代码]¶

所有后端的基类。后端代表绘图库，它实现了使用 SymPy 绘图函数所需的功能。

对于交互式工作，函数 plot() 更为合适。

此类允许使用多种后端（matplotlib、textplot、SymPy 的旧 pyglet 模块、Google charts api 等）绘制 SymPy 表达式。

该图形可以包含任意数量的 SymPy 表达式、点坐标列表等的绘图。Plot 有一个私有属性 _series，其中包含所有要绘制的数据系列（线条或曲面的表达式、点列表等（所有 BaseSeries 的子类））。这些数据系列是类的实例，不会被 from sympy import * 导入。

图形的定制分为两个层次。全局选项涉及整个图形（例如标题、x轴标签、比例等），以及每个数据系列的选项（例如名称）和美学（例如颜色、点形状、线条类型等）。

选项和美学之间的区别在于，美学可以是坐标的函数（或在参数图中是参数的函数）。美学的支持值为：

无（后端使用默认值）
一个常量
一个变量的函数（第一个坐标或参数）
两个变量的函数（第一个和第二个坐标或参数）
三个变量的函数（仅在非参数 3D 图中）

它们的实现依赖于后端，因此在某些后端中可能无法工作。

如果图是参数化的，并且美学函数的元数允许，则美学是基于参数而不是坐标计算的。如果元数不允许基于参数计算，则计算基于坐标进行。

目前仅支持笛卡尔坐标，但您可以使用参数化绘图在极坐标、球坐标和柱坐标中绘图。

构造函数 Plot 的参数必须是 BaseSeries 的子类。

任何全局选项都可以指定为关键字参数。

图形的全局选项包括：

title : str
xlabel : str 或 Symbol
ylabel : str 或 Symbol
zlabel : str 或 Symbol
legend : bool
xscale : {‘linear’, ‘log’}
yscale : {‘linear’, ‘log’}
axis : bool
axis_center : 两个浮点数的元组或 {‘center’, ‘auto’}
xlim : 两个浮点数的元组
ylim : 两个浮点数的元组
aspect_ratio : 两个浮点数的元组或 {‘auto’}
autoscale : bool
margin : float in [0, 1]
backend : {‘default’, ‘matplotlib’, ‘text’} 或 BaseBackend 的子类
size : 可选的两个浮点数的元组，(宽度, 高度); 默认: None

每个数据系列选项和美学效果如下：基本系列中没有。子类的选项请参见下文。

一些数据系列支持额外的审美或选项：

LineOver1DRangeSeries, Parametric2DLineSeries, 和 Parametric3DLineSeries 支持以下内容：

美学：

line_color字符串，或浮点数，或函数，可选
指定绘图的颜色，这取决于所使用的后端。

例如，如果正在使用 MatplotlibBackend ，那么 Matplotlib 字符串颜色是可以接受的（例如 "red"、"r"、"cyan"、"c" 等）。或者，我们可以使用一个浮点数，0 < color < 1，包裹在字符串中（例如，line_color="0.5"）来指定灰度颜色。另外，我们可以指定一个返回单个浮点值的函数：这将用于应用颜色循环（例如，line_color=lambda x: math.cos(x)）。

请注意，通过设置 line_color，它将同时应用于所有系列。

选项：

label : str
steps : bool
integers_only : bool

SurfaceOver2DRangeSeries 和 ParametricSurfaceSeries 支持以下内容：

美学：

surface_color : 返回浮点数的函数。

属性:

annotations: 自 1.13 版本弃用.
后端
fill: 自 1.13 版本弃用.
markers: 自 1.13 版本弃用.
rectangles: 自 1.13 版本弃用.

方法

`append`(arg)	将图表系列中的一个元素添加到现有图表中。
`extend`(arg)	添加来自另一个图表的所有系列。

关闭
保存
显示

注释

绘图模块的工作原理：

每当调用绘图函数时，提供的表达式会被处理，并创建一个 BaseSeries 类的实例列表，其中包含绘制表达式所需的信息（例如表达式、范围、序列名称等）。最终，这些对象将生成要绘制的数值数据。
一个 Plot 类的子类被实例化（从现在起称为后端），它存储了系列列表和图表的主要属性（例如轴标签、标题等）。后端实现了使用某些绘图库生成实际图形的逻辑。
当执行 show 命令时，系列数据会逐一处理以生成数值数据并将其添加到图形中。后端还会根据 Plot 实例中存储的值设置轴标签、标题等。

后端应检查其是否支持所给定的数据系列（例如，TextBackend 仅支持 LineOver1DRangeSeries）。

后端的责任是知道如何使用它所接收到的数据系列类。请注意，当前 *Series 类的实现是“以 Matplotlib 为中心”的：get_points 和 get_meshes 方法返回的数值数据旨在直接由 Matplotlib 使用。因此，新的后端将需要预处理数值数据，以使其与所选的绘图库兼容。请记住，未来的 SymPy 版本可能会改进 *Series 类，以便返回“非 Matplotlib 为中心”的数值数据，因此，如果您编写一个新的后端，您有责任在每次 SymPy 发布时检查其工作情况。

请探索 MatplotlibBackend 源代码，以了解如何编写后端。

为了被 SymPy 绘图函数使用，后端必须实现以下方法：

show(self): 用于遍历数据系列，生成数值
数据，绘制它并设置轴标签、标题，…
save(self, path): 用于将当前图形保存到指定文件
路径。
close(self): 用于关闭当前的绘图后端（注意：某些绘图
库不支持此功能。在这种情况下，只需引发警告）。

property annotations¶: 自 1.13 版本弃用.

append(arg)[源代码][源代码]¶

将图表系列中的一个元素添加到现有图表中。

参见

extend

示例

考虑两个 Plot 对象，p1 和 p2。要将第二个图的第一个系列对象添加到第一个图，使用 append 方法，如下所示：

>>> from sympy import symbols
>>> from sympy.plotting import plot
>>> x = symbols('x')
>>> p1 = plot(x*x, show=False)
>>> p2 = plot(x, show=False)
>>> p1.append(p2[0])
>>> p1
Plot object containing:
[0]: cartesian line: x**2 for x over (-10.0, 10.0)
[1]: cartesian line: x for x over (-10.0, 10.0)
>>> p1.show()

(png, hires.png, pdf)

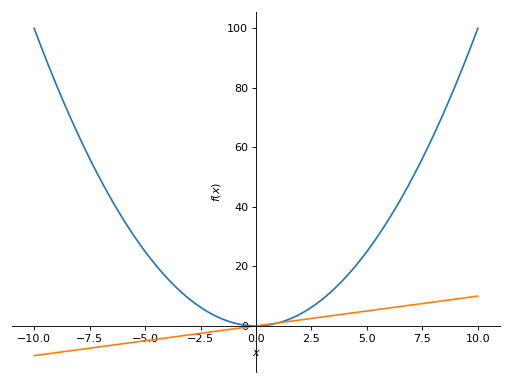
extend(arg)[源代码][源代码]¶

添加来自另一个图表的所有系列。

示例

考虑两个 Plot 对象，p1 和 p2。要将第二个图添加到第一个图，请使用 extend 方法，如下所示：

>>> from sympy import symbols
>>> from sympy.plotting import plot
>>> x = symbols('x')
>>> p1 = plot(x**2, show=False)
>>> p2 = plot(x, -x, show=False)
>>> p1.extend(p2)
>>> p1
Plot object containing:
[0]: cartesian line: x**2 for x over (-10.0, 10.0)
[1]: cartesian line: x for x over (-10.0, 10.0)
[2]: cartesian line: -x for x over (-10.0, 10.0)
>>> p1.show()

(png, hires.png, pdf)

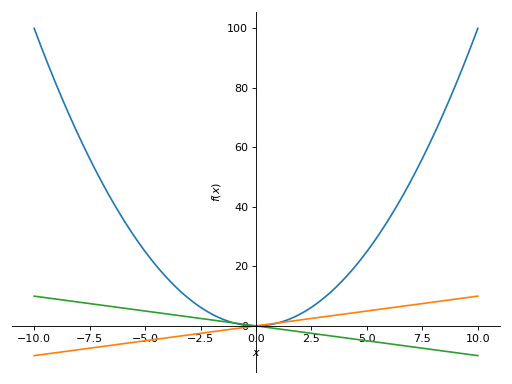
property fill¶: 自 1.13 版本弃用.

property markers¶: 自 1.13 版本弃用.

property rectangles¶: 自 1.13 版本弃用.

绘图函数参考¶

sympy.plotting.plot.plot(*args, show=True, **kwargs)[源代码][源代码]¶

绘制单变量函数的曲线。

参数:

参数

第一个参数是表示要绘制的一元函数表达式。

最后一个参数是一个表示自由变量范围的3元组。例如 (x, 0, 5)

典型的使用示例如下：

绘制单个表达式与单个范围。
plot(expr, range, **kwargs)
使用默认范围 (-10, 10) 绘制单个表达式。
plot(expr, **kwargs)
使用单个范围绘制多个表达式。
plot(expr1, expr2, ..., range, **kwargs)
使用多个范围绘制多个表达式。
plot((expr1, range1), (expr2, range2), ..., **kwargs)

最好明确指定范围，因为如果将来实现了更高级的默认范围检测算法，默认范围可能会发生变化。

显示bool, 可选

默认值设置为 True。将 show 设置为 False，函数将不会显示图表。然后可以使用 Plot 类的返回实例分别调用 save() 和 show() 方法来保存或显示图表。

line_color字符串，或浮点数，或函数，可选

指定图表的颜色。请参阅 Plot 以了解如何为图表设置颜色。请注意，通过设置 line_color，它将同时应用于所有系列。

标题str, 可选

图的标题。如果图只有一个表达式，则设置为该表达式的latex表示。

标签str, 可选

图中表达式的标签。当使用 legend 调用时将使用此标签。默认是表达式的名称。例如 sin(x)

xlabelstr 或表达式，可选

x轴的标签。

ylabelstr 或表达式，可选

y轴的标签。

xscale‘线性’ 或 ‘对数’, 可选

设置 x 轴的缩放比例。

yscale‘线性’ 或 ‘对数’, 可选

设置 y 轴的缩放比例。

axis_center(浮点数, 浮点数), 可选

由两个浮点数组成的元组，表示中心的坐标，或 {‘center’, ‘auto’}

xlim(浮点数, 浮点数), 可选

表示 x 轴的范围，(最小值, 最大值)`。

ylim(浮点数, 浮点数), 可选

表示 y 轴的限制，(min, max)`。

注解列表，可选

指定所需注释类型的字典列表。字典中的键应与 matplotlib 的 annotate() 方法的参数等效。

标记列表，可选

指定所需标记类型的字典列表。字典中的键应等同于 matplotlib 的 plot() 函数的参数，以及与标记相关的关键字参数。

矩形列表，可选

指定要绘制的矩形尺寸的字典列表。字典中的键应等同于 matplotlib 的 Rectangle 类的参数。

填充dict, 可选

一个指定绘图中所需颜色填充类型的字典。字典中的键应与 matplotlib 的 fill_between() 方法的参数等效。

自适应bool, 可选

默认值设置为 True。如果需要均匀采样，请将 adaptive 设置为 False 并指定 n。

绘图使用了一种自适应算法，该算法递归采样以准确绘图。自适应算法在需要进一步采样的两点中点附近使用一个随机点。因此，相同的绘图可能会略有不同。

深度int, 可选

自适应算法的递归深度。深度值为 $n$ 时，最多采样 $2^{n}$ 个点。

如果 adaptive 标志设置为 False ，这将忽略。

nint, 可选

当 adaptive 设置为 False 时使用。该函数在 n 个点上均匀采样。如果 adaptive 标志设置为 True ，这将忽略。此关键字参数取代了 nb_of_points ，应视为已弃用。

大小(浮点数, 浮点数), 可选

以 (宽度, 高度) 形式的元组，单位为英寸，用于指定整个图形的大小。默认值设置为 None，这意味着大小将由默认的后端设置。

参见

Plot, LineOver1DRangeSeries

示例

>>> from sympy import symbols
>>> from sympy.plotting import plot
>>> x = symbols('x')

单图

>>> plot(x**2, (x, -5, 5))
Plot object containing:
[0]: cartesian line: x**2 for x over (-5.0, 5.0)

(png, hires.png, pdf)

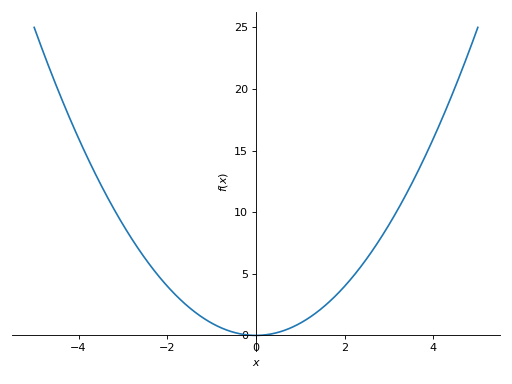
单范围多图表。

>>> plot(x, x**2, x**3, (x, -5, 5))
Plot object containing:
[0]: cartesian line: x for x over (-5.0, 5.0)
[1]: cartesian line: x**2 for x over (-5.0, 5.0)
[2]: cartesian line: x**3 for x over (-5.0, 5.0)

(png, hires.png, pdf)

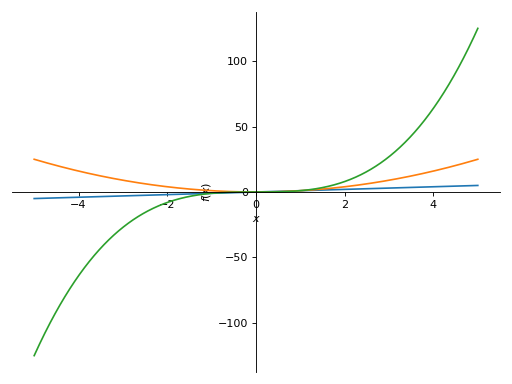
具有不同范围的多个图表。

>>> plot((x**2, (x, -6, 6)), (x, (x, -5, 5)))
Plot object containing:
[0]: cartesian line: x**2 for x over (-6.0, 6.0)
[1]: cartesian line: x for x over (-5.0, 5.0)

(png, hires.png, pdf)

无自适应采样。

>>> plot(x**2, adaptive=False, n=400)
Plot object containing:
[0]: cartesian line: x**2 for x over (-10.0, 10.0)

(png, hires.png, pdf)

sympy.plotting.plot.plot_parametric(*args, show=True, **kwargs)[源代码][源代码]¶

绘制一个二维参数曲线。

参数:

参数

常见的规范包括：

绘制单个参数曲线的范围
plot_parametric((expr_x, expr_y), range)
在相同范围内绘制多条参数曲线
plot_parametric((expr_x, expr_y), ..., range)
绘制具有不同范围的多条参数曲线
plot_parametric((expr_x, expr_y, range), ...)

expr_x 是表示参数函数 $x$ 分量的表达式。

expr_y 是表示参数函数的 $y$ 分量的表达式。

range 是一个三元组，表示参数符号、起始和终止。例如，(u, 0, 5)。

如果没有指定范围，则使用默认范围 (-10, 10)。

然而，如果参数被指定为 (expr_x, expr_y, range), ...，你必须手动为每个表达式指定范围。

如果将来实施了更高级的算法，默认范围可能会发生变化。

自适应bool, 可选

指定是否使用自适应采样。

默认值设置为 True。如果需要均匀采样，请将 adaptive 设置为 False 并指定 n。

深度int, 可选

自适应算法的递归深度。深度值为 $n$ 时，最多采样 $2^n$ 个点。

nint, 可选

当 adaptive 标志设置为 False 时使用。指定用于均匀采样的点的数量。此关键字参数取代了 nb_of_points，后者应被视为已弃用。

line_color字符串，或浮点数，或函数，可选

指定图表的颜色。请参阅 Plot 以了解如何为图表设置颜色。请注意，通过设置 line_color，它将同时应用于所有系列。

标签str, 可选

图中表达式的标签。当使用 legend 调用时将使用此标签。默认是表达式的名称。例如 sin(x)

xlabelstr, 可选

x轴的标签。

ylabelstr, 可选

y轴的标签。

xscale‘线性’ 或 ‘对数’, 可选

设置 x 轴的缩放比例。

yscale‘线性’ 或 ‘对数’, 可选

设置 y 轴的缩放比例。

axis_center(浮点数, 浮点数), 可选

由两个浮点数组成的元组，表示中心的坐标，或 {‘center’, ‘auto’}

xlim(浮点数, 浮点数), 可选

表示 x 轴的范围，(最小值, 最大值)`。

ylim(浮点数, 浮点数), 可选

表示 y 轴的限制，(min, max)`。

大小(浮点数, 浮点数), 可选

以 (宽度, 高度) 形式的元组，单位为英寸，用于指定整个图形的大小。默认值设置为 None，这意味着大小将由默认的后端设置。

参见

Plot, Parametric2DLineSeries

注释

绘图使用了一种自适应算法，该算法递归采样以准确绘制曲线。自适应算法在需要进一步采样的两点中点附近使用一个随机点。因此，重复相同的绘图命令可能会因为随机采样而得到略有不同的结果。

如果有多个图表，那么相同的可选参数将应用于同一画布上绘制的所有图表。如果你想单独设置这些选项，可以索引返回的 Plot 对象并进行设置。

例如，当你指定 line_color 一次时，它将同时应用于两个系列。

>>> from sympy import pi
>>> expr1 = (u, cos(2*pi*u)/2 + 1/2)
>>> expr2 = (u, sin(2*pi*u)/2 + 1/2)
>>> p = plot_parametric(expr1, expr2, (u, 0, 1), line_color='blue')

如果你想为特定的系列指定线条颜色，你应该为每个项目建立索引并手动应用该属性。

>>> p[0].line_color = 'red'
>>> p.show()

(png, hires.png, pdf)

示例

>>> from sympy import plot_parametric, symbols, cos, sin
>>> u = symbols('u')

带有单个表达式的参数化绘图：

>>> plot_parametric((cos(u), sin(u)), (u, -5, 5))
Plot object containing:
[0]: parametric cartesian line: (cos(u), sin(u)) for u over (-5.0, 5.0)

(png, hires.png, pdf)

具有相同范围的多个表达式的参数图：

>>> plot_parametric((cos(u), sin(u)), (u, cos(u)), (u, -10, 10))
Plot object containing:
[0]: parametric cartesian line: (cos(u), sin(u)) for u over (-10.0, 10.0)
[1]: parametric cartesian line: (u, cos(u)) for u over (-10.0, 10.0)

(png, hires.png, pdf)

带有多个表达式的参数图，每个曲线有不同的范围：

>>> plot_parametric((cos(u), sin(u), (u, -5, 5)),
...     (cos(u), u, (u, -5, 5)))
Plot object containing:
[0]: parametric cartesian line: (cos(u), sin(u)) for u over (-5.0, 5.0)
[1]: parametric cartesian line: (cos(u), u) for u over (-5.0, 5.0)

(png, hires.png, pdf)

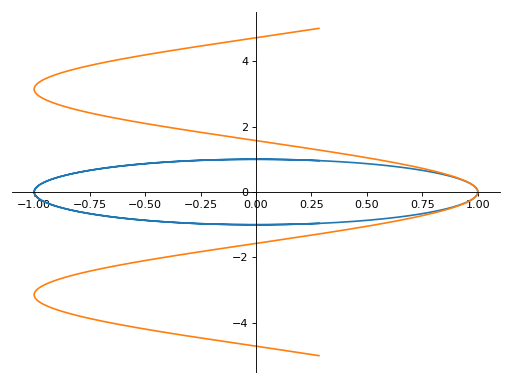
sympy.plotting.plot.plot3d(*args, show=True, **kwargs)[源代码][源代码]¶

绘制一个3D表面图。

参见

Plot, SurfaceOver2DRangeSeries

示例

>>> from sympy import symbols
>>> from sympy.plotting import plot3d
>>> x, y = symbols('x y')

单个图表

>>> plot3d(x*y, (x, -5, 5), (y, -5, 5))
Plot object containing:
[0]: cartesian surface: x*y for x over (-5.0, 5.0) and y over (-5.0, 5.0)

(png, hires.png, pdf)

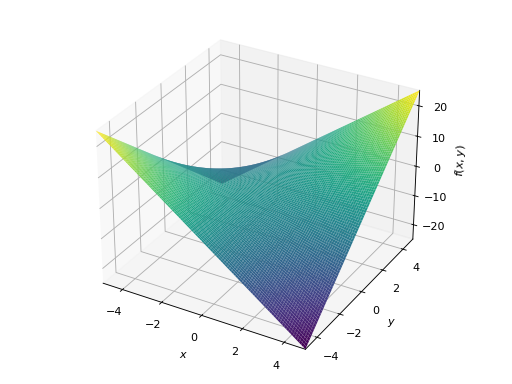
具有相同范围的多个图表

>>> plot3d(x*y, -x*y, (x, -5, 5), (y, -5, 5))
Plot object containing:
[0]: cartesian surface: x*y for x over (-5.0, 5.0) and y over (-5.0, 5.0)
[1]: cartesian surface: -x*y for x over (-5.0, 5.0) and y over (-5.0, 5.0)

(png, hires.png, pdf)

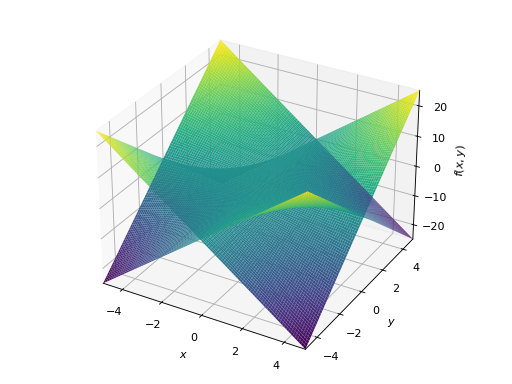
具有不同范围的多个图表。

>>> plot3d((x**2 + y**2, (x, -5, 5), (y, -5, 5)),
...     (x*y, (x, -3, 3), (y, -3, 3)))
Plot object containing:
[0]: cartesian surface: x**2 + y**2 for x over (-5.0, 5.0) and y over (-5.0, 5.0)
[1]: cartesian surface: x*y for x over (-3.0, 3.0) and y over (-3.0, 3.0)

(png, hires.png, pdf)

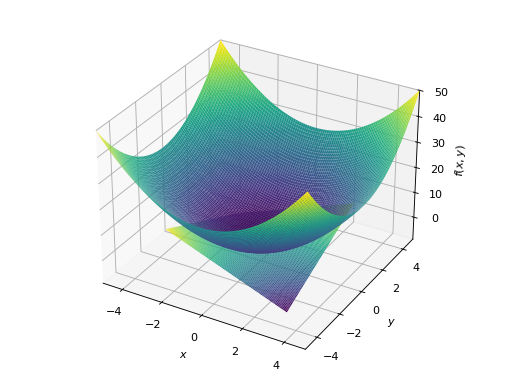
sympy.plotting.plot.plot3d_parametric_line(*args, show=True, **kwargs)[源代码][源代码]¶

绘制一个三维参数线图。

参见

Plot, Parametric3DLineSeries

示例

>>> from sympy import symbols, cos, sin
>>> from sympy.plotting import plot3d_parametric_line
>>> u = symbols('u')

单个图表。

>>> plot3d_parametric_line(cos(u), sin(u), u, (u, -5, 5))
Plot object containing:
[0]: 3D parametric cartesian line: (cos(u), sin(u), u) for u over (-5.0, 5.0)

(png, hires.png, pdf)

多图表。

>>> plot3d_parametric_line((cos(u), sin(u), u, (u, -5, 5)),
...     (sin(u), u**2, u, (u, -5, 5)))
Plot object containing:
[0]: 3D parametric cartesian line: (cos(u), sin(u), u) for u over (-5.0, 5.0)
[1]: 3D parametric cartesian line: (sin(u), u**2, u) for u over (-5.0, 5.0)

(png, hires.png, pdf)

sympy.plotting.plot.plot3d_parametric_surface(

*args,

show=True,

**kwargs,

)[源代码][源代码]¶

绘制一个三维参数化曲面图。

参见

Plot, ParametricSurfaceSeries

示例

>>> from sympy import symbols, cos, sin
>>> from sympy.plotting import plot3d_parametric_surface
>>> u, v = symbols('u v')

单个图表。

>>> plot3d_parametric_surface(cos(u + v), sin(u - v), u - v,
...     (u, -5, 5), (v, -5, 5))
Plot object containing:
[0]: parametric cartesian surface: (cos(u + v), sin(u - v), u - v) for u over (-5.0, 5.0) and v over (-5.0, 5.0)

(png, hires.png, pdf)

sympy.plotting.plot_implicit.plot_implicit(

expr,

x_var=None,

y_var=None,

adaptive=True,

depth=0,

n=300,

line_color='blue',

show=True,

**kwargs,

)[源代码][源代码]¶

一个用于绘制隐式方程/不等式的绘图函数。

示例

绘图表达式：

>>> from sympy import plot_implicit, symbols, Eq, And
>>> x, y = symbols('x y')

在表达式中没有任何符号的范围：

>>> p1 = plot_implicit(Eq(x**2 + y**2, 5))

(png, hires.png, pdf)

使用符号的范围：

>>> p2 = plot_implicit(
...     Eq(x**2 + y**2, 3), (x, -3, 3), (y, -3, 3))

(png, hires.png, pdf)

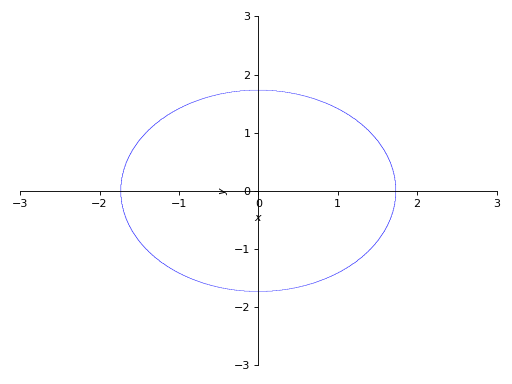
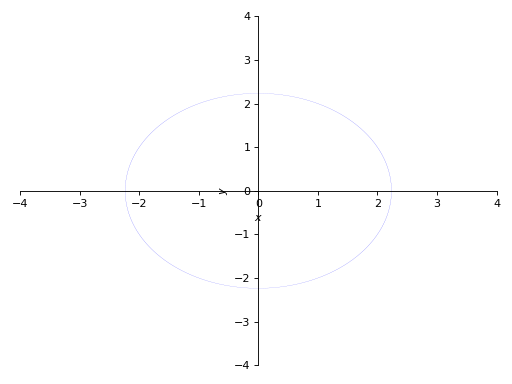
以递归深度为参数：

>>> p3 = plot_implicit(
...     Eq(x**2 + y**2, 5), (x, -4, 4), (y, -4, 4), depth = 2)

(png, hires.png, pdf)

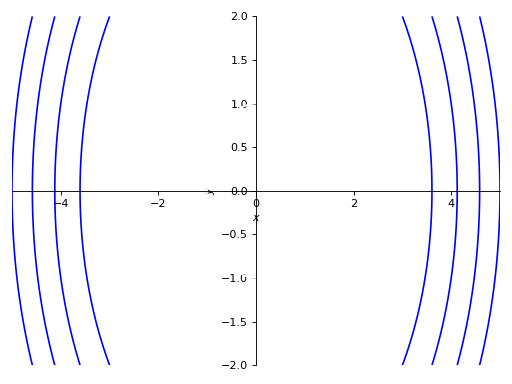
使用网格和非自适应网格：

>>> p4 = plot_implicit(
...     Eq(x**2 + y**2, 5), (x, -5, 5), (y, -2, 2),
...     adaptive=False)

(png, hires.png, pdf)

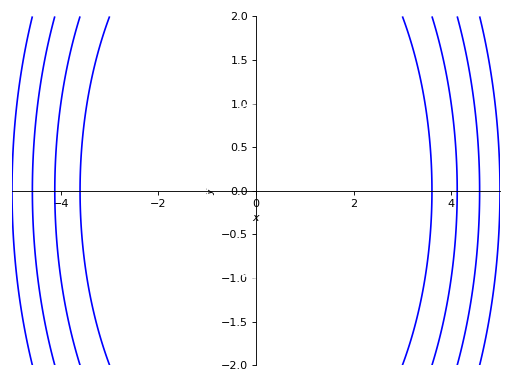
使用网格而不使用自适应网格，指定点的数量：

>>> p5 = plot_implicit(
...     Eq(x**2 + y**2, 5), (x, -5, 5), (y, -2, 2),
...     adaptive=False, n=400)

(png, hires.png, pdf)

绘制区域：

>>> p6 = plot_implicit(y > x**2)

(png, hires.png, pdf)

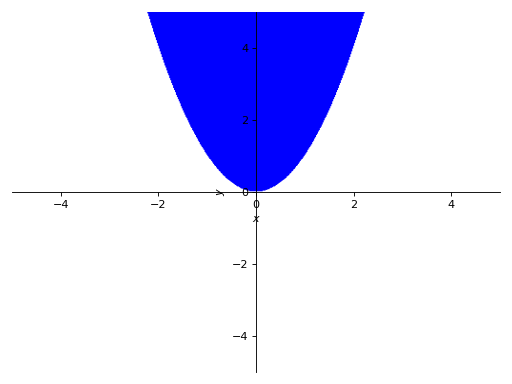
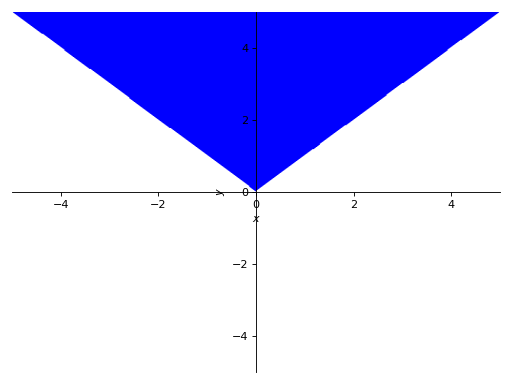
使用布尔连接词绘图：

>>> p7 = plot_implicit(And(y > x, y > -x))

(png, hires.png, pdf)

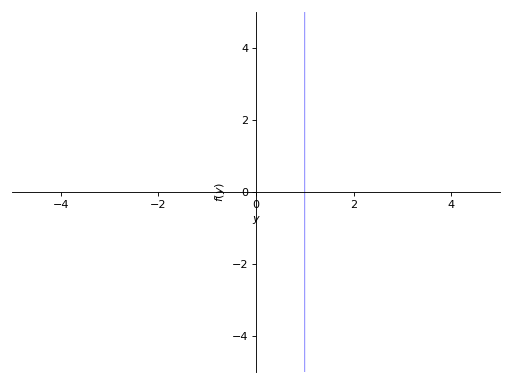
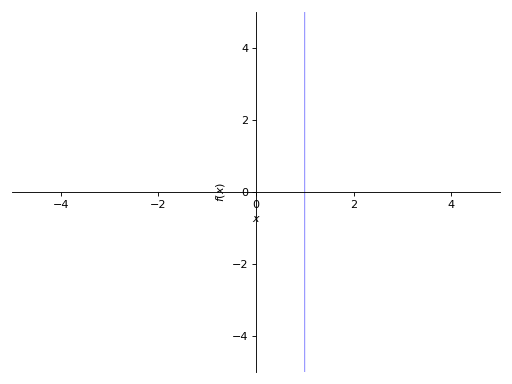
在绘制单变量表达式（例如 y - 1）时，请明确指定 x 或 y 变量：

>>> p8 = plot_implicit(y - 1, y_var=y)
>>> p9 = plot_implicit(x - 1, x_var=x)

../_images/plotting-31_00.png — (`png`, `hires.png`, `pdf`)¶

../_images/plotting-31_01.png — (`png`, `hires.png`, `pdf`)¶

PlotGrid 类¶

class sympy.plotting.plot.PlotGrid(

nrows,

ncolumns,

*args,

show=True,

size=None,

**kwargs,

)[源代码][源代码]¶

此类有助于在单个图形中绘制从已创建的 SymPy 绘图中生成的子图。

属性:

图

方法

关闭
保存
显示

示例

>>> from sympy import symbols
>>> from sympy.plotting import plot, plot3d, PlotGrid
>>> x, y = symbols('x, y')
>>> p1 = plot(x, x**2, x**3, (x, -5, 5))
>>> p2 = plot((x**2, (x, -6, 6)), (x, (x, -5, 5)))
>>> p3 = plot(x**3, (x, -5, 5))
>>> p4 = plot3d(x*y, (x, -5, 5), (y, -5, 5))

../_images/plotting-32_00.png — (`png`, `hires.png`, `pdf`)¶

../_images/plotting-32_01.png — (`png`, `hires.png`, `pdf`)¶

../_images/plotting-32_02.png — (`png`, `hires.png`, `pdf`)¶

../_images/plotting-32_03.png — (`png`, `hires.png`, `pdf`)¶

在单行中垂直绘制：

>>> PlotGrid(2, 1, p1, p2)
PlotGrid object containing:
Plot[0]:Plot object containing:
[0]: cartesian line: x for x over (-5.0, 5.0)
[1]: cartesian line: x**2 for x over (-5.0, 5.0)
[2]: cartesian line: x**3 for x over (-5.0, 5.0)
Plot[1]:Plot object containing:
[0]: cartesian line: x**2 for x over (-6.0, 6.0)
[1]: cartesian line: x for x over (-5.0, 5.0)

(png, hires.png, pdf)

在单行中水平绘图：

>>> PlotGrid(1, 3, p2, p3, p4)
PlotGrid object containing:
Plot[0]:Plot object containing:
[0]: cartesian line: x**2 for x over (-6.0, 6.0)
[1]: cartesian line: x for x over (-5.0, 5.0)
Plot[1]:Plot object containing:
[0]: cartesian line: x**3 for x over (-5.0, 5.0)
Plot[2]:Plot object containing:
[0]: cartesian surface: x*y for x over (-5.0, 5.0) and y over (-5.0, 5.0)

(png, hires.png, pdf)

以网格形式绘图：

>>> PlotGrid(2, 2, p1, p2, p3, p4)
PlotGrid object containing:
Plot[0]:Plot object containing:
[0]: cartesian line: x for x over (-5.0, 5.0)
[1]: cartesian line: x**2 for x over (-5.0, 5.0)
[2]: cartesian line: x**3 for x over (-5.0, 5.0)
Plot[1]:Plot object containing:
[0]: cartesian line: x**2 for x over (-6.0, 6.0)
[1]: cartesian line: x for x over (-5.0, 5.0)
Plot[2]:Plot object containing:
[0]: cartesian line: x**3 for x over (-5.0, 5.0)
Plot[3]:Plot object containing:
[0]: cartesian surface: x*y for x over (-5.0, 5.0) and y over (-5.0, 5.0)

(png, hires.png, pdf)

系列类¶

class sympy.plotting.series.BaseSeries(*args, **kwargs)[源代码][源代码]¶

包含要绘制内容的基类数据对象。

属性:

expr: 返回序列的表达式（或多个表达式）。
is_3D
is_line
标签
line_color
n: 返回一个离散点数的列表 [n1, n2, n3]。
params: 获取或设置当前参数字典。
范围
rendering_kw
刻度
表面颜色

方法

`eval_color_func`(*args)	评估颜色函数。
`get_data`()	计算并返回数值数据。
`get_label`([use_latex, wrapper])	返回用于显示表达式的标签。

注释

后端应检查其是否支持给定的数据系列。（例如，TextBackend 仅支持 LineOver1DRangeSeries）。后端有责任知道如何使用给定的数据系列类。

一些数据系列类根据它们呈现的API（仅基于约定）被分组（使用类似is_2Dline的类属性）。后端不必使用该API（例如，LineOver1DRangeSeries属于is_2Dline组并呈现get_points方法，但TextBackend不使用get_points方法）。

BaseSeries

eval_color_func(*args)[源代码][源代码]¶

评估颜色函数。

参数:

参数元组: 传递给着色函数的参数。可以是坐标或参数，或两者兼有。

注释

后端将请求数据系列以生成数值数据。根据数据系列的不同，数据系列本身或后端最终将执行此函数以生成适当的着色值。

property expr¶: 返回序列的表达式（或多个表达式）。

get_data()[源代码][源代码]¶

计算并返回数值数据。

此方法返回的参数数量取决于具体的实例。如果 s 是序列，请确保阅读 help(s.get_data) 以了解它返回的内容。

get_label( use_latex=False, wrapper='$%s$', )[源代码][源代码]¶

返回用于显示表达式的标签。

参数:

use_latex布尔: 如果为 False，则返回表达式的字符串表示。如果为 True，则返回 latex 表示。
包装器str: 后端可能需要将latex表示用某些字符包裹。默认为 "$%s$"。

返回:

标签str

property n¶: 返回一个离散点数的列表 [n1, n2, n3]。

property params¶

获取或设置当前参数字典。

参数:

pdict

键: 与参数关联的符号
val: 数值

class sympy.plotting.series.Line2DBaseSeries(**kwargs)[源代码][源代码]¶

一个用于2D线条的基类。

添加标签、步骤和 only_integers 选项
将 is_2Dline 设为真
定义 get_segments 和 get_color_array

属性:

结束
expr: 返回序列的表达式（或多个表达式）。
is_3D
is_line
标签
line_color
n: 返回一个离散点数的列表 [n1, n2, n3]。
params: 获取或设置当前参数字典。
范围
rendering_kw
刻度
开始
表面颜色
变量
xscale

方法

`eval_color_func`(*args)	评估颜色函数。
`get_data`()	返回用于绘制线条的坐标。
`get_label`([use_latex, wrapper])	返回用于显示表达式的标签。

get_color_array
get_segments

get_data()[源代码][源代码]¶

返回用于绘制线条的坐标。

返回:

x: np.ndarray: x-坐标
y: np.ndarray: y-坐标
z: np.ndarray (可选): 在 Parametric3DLineSeries, Parametric3DLineInteractiveSeries 的情况下，z-coordinates
参数np.ndarray (可选): 在 Parametric2DLineSeries、Parametric3DLineSeries 或 AbsArgLineSeries（及其相应的交互系列）的情况下，参数。

class sympy.plotting.series.LineOver1DRangeSeries(

expr,

var_start_end,

label='',

**kwargs,

)[源代码][源代码]¶

表示由 SymPy 表达式组成的行，覆盖一个范围。

属性:

结束
expr: 返回序列的表达式（或多个表达式）。
is_3D
is_line
标签
line_color
n: 返回一个离散点数的列表 [n1, n2, n3]。
nb_of_points
params: 获取或设置当前参数字典。
范围
rendering_kw
刻度
开始
表面颜色
变量
xscale

方法

`eval_color_func`(*args)	评估颜色函数。
`get_data`()	返回用于绘制线条的坐标。
`get_label`([use_latex, wrapper])	返回用于显示表达式的标签。
`get_points`()	返回用于绘图的坐标列表。

get_color_array
get_segments

get_points()[源代码][源代码]¶

返回用于绘图的坐标列表。根据 adaptive 选项，此函数将使用自适应算法，或者在提供的范围内均匀采样表达式。

此函数出于向后兼容的目的而可用。建议改用 get_data()。

返回:

x列表: x坐标列表
y列表: y坐标列表

class sympy.plotting.series.Parametric2DLineSeries(

expr_x,

expr_y,

var_start_end,

label='',

**kwargs,

)[源代码][源代码]¶

表示由两个参数化 SymPy 表达式组成的线的表示形式，覆盖一个范围。

属性:

结束
expr: 返回序列的表达式（或多个表达式）。
is_3D
is_line
标签
line_color
n: 返回一个离散点数的列表 [n1, n2, n3]。
nb_of_points
params: 获取或设置当前参数字典。
范围
rendering_kw
刻度
开始
表面颜色
变量
xscale

方法

`eval_color_func`(*args)	评估颜色函数。
`get_data`()	返回用于绘制线条的坐标。
`get_label`([use_latex, wrapper])
`get_points`()	返回用于绘图的坐标列表。

get_color_array
get_parameter_points
get_segments

class sympy.plotting.series.Line3DBaseSeries[源代码][源代码]¶

一个用于3D线条的基类。

大部分内容源自 Line2DBaseSeries。

属性:

结束
expr: 返回序列的表达式（或多个表达式）。
is_3D
is_line
标签
line_color
n: 返回一个离散点数的列表 [n1, n2, n3]。
params: 获取或设置当前参数字典。
范围
rendering_kw
刻度
开始
表面颜色
变量
xscale

方法

`eval_color_func`(*args)	评估颜色函数。
`get_data`()	返回用于绘制线条的坐标。
`get_label`([use_latex, wrapper])	返回用于显示表达式的标签。

get_color_array
get_segments

class sympy.plotting.series.Parametric3DLineSeries(

expr_x,

expr_y,

expr_z,

var_start_end,

label='',

**kwargs,

)[源代码][源代码]¶

表示由三个参数化的 SymPy 表达式和一个范围组成的 3D 线的表示。

属性:

结束
expr: 返回序列的表达式（或多个表达式）。
is_3D
is_line
标签
line_color
n: 返回一个离散点数的列表 [n1, n2, n3]。
nb_of_points
params: 获取或设置当前参数字典。
范围
rendering_kw
刻度
开始
表面颜色
变量
xscale

方法

`eval_color_func`(*args)	评估颜色函数。
`get_data`()
`get_label`([use_latex, wrapper])
`get_points`()	返回用于绘图的坐标列表。

get_color_array
get_parameter_points
get_segments

class sympy.plotting.series.SurfaceBaseSeries(*args, **kwargs)[源代码][源代码]¶

一个用于3D曲面的基类。

属性:

expr: 返回序列的表达式（或多个表达式）。
is_3D
is_line
标签
line_color
n: 返回一个离散点数的列表 [n1, n2, n3]。
params: 获取或设置当前参数字典。
范围
rendering_kw
刻度
表面颜色

方法

`eval_color_func`(*args)	评估颜色函数。
`get_data`()	计算并返回数值数据。
`get_label`([use_latex, wrapper])	返回用于显示表达式的标签。

get_color_array

class sympy.plotting.series.SurfaceOver2DRangeSeries(

expr,

var_start_end_x,

var_start_end_y,

label='',

**kwargs,

)[源代码][源代码]¶

表示由 SymPy 表达式和二维范围组成的 3D 曲面。

属性:

end_x
end_y
expr: 返回序列的表达式（或多个表达式）。
is_3D
is_line
标签
line_color
n: 返回一个离散点数的列表 [n1, n2, n3]。
nb_of_points_x
nb_of_points_y
params: 获取或设置当前参数字典。
范围
rendering_kw
刻度
start_x
start_y
表面颜色
var_x
var_y

方法

`eval_color_func`(*args)	评估颜色函数。
`get_data`()	返回用于绘图的坐标数组。
`get_label`([use_latex, wrapper])	返回用于显示表达式的标签。
`get_meshes`()	返回用于绘制表面的 x,y,z 坐标。

get_color_array

get_data()[源代码][源代码]¶

返回用于绘图的坐标数组。

返回:

mesh_xnp.ndarray: 离散化的 x 域。
网格_ynp.ndarray: 离散化的 y 域。
mesh_znp.ndarray: 评估结果。

get_meshes()[源代码][源代码]¶: 返回用于绘制表面的 x,y,z 坐标。此函数用于向后兼容。建议使用 get_data() 代替。

class sympy.plotting.series.ParametricSurfaceSeries(

expr_x,

expr_y,

expr_z,

var_start_end_u,

var_start_end_v,

label='',

**kwargs,

)[源代码][源代码]¶

由三个参数化的 SymPy 表达式和一个范围组成的 3D 曲面表示。

属性:

end_u
end_v
expr: 返回序列的表达式（或多个表达式）。
is_3D
is_line
标签
line_color
n: 返回一个离散点数的列表 [n1, n2, n3]。
nb_of_points_u
nb_of_points_v
params: 获取或设置当前参数字典。
范围
rendering_kw
刻度
start_u
start_v
表面颜色
var_u
var_v

方法

`eval_color_func`(*args)	评估颜色函数。
`get_data`()	返回用于绘图的坐标数组。
`get_label`([use_latex, wrapper])	返回用于显示表达式的标签。
`get_meshes`()	返回用于绘制表面的 x,y,z 坐标。

get_color_array
get_parameter_meshes

get_data()[源代码][源代码]¶

返回用于绘图的坐标数组。

返回:

xnp.ndarray [n2 x n1]: x-坐标。
ynp.ndarray [n2 x n1]: y-坐标。
znp.ndarray [n2 x n1]: z-坐标。
mesh_unp.ndarray [n2 x n1]: 离散化的 u 范围。
mesh_vnp.ndarray [n2 x n1]: 离散化的 v 范围。

get_meshes()[源代码][源代码]¶: 返回用于绘制表面的 x,y,z 坐标。此函数用于向后兼容。建议使用 get_data() 代替。

class sympy.plotting.series.ImplicitSeries(

expr,

var_start_end_x,

var_start_end_y,

label='',

**kwargs,

)[源代码][源代码]¶

二维隐式图的表示。

属性:

颜色
expr: 返回序列的表达式（或多个表达式）。
is_3D
is_line
标签
line_color
n: 返回一个离散点数的列表 [n1, n2, n3]。
params: 获取或设置当前参数字典。
范围
rendering_kw
刻度
表面颜色

方法

`eval_color_func`(*args)	评估颜色函数。
`get_data`()	返回数值数据。
`get_label`([use_latex, wrapper])	返回用于显示表达式的标签。

get_data()[源代码][源代码]¶

返回数值数据。

返回:

如果使用 $adaptive=True$ 评估序列，它将返回：
interval_list列表: 要进行后处理的边界矩形区间列表，最终与 Matplotlib 的 fill 命令一起使用。
dummystr: 包含 "fill" 的字符串。
否则，它返回2D numpy数组以与Matplotlib一起使用。
contour 或 contourf 命令：
x_arraynp.ndarray
y_arraynp.ndarray
z_arraynp.ndarray
plot_typestr: 指定使用哪个绘图命令的字符串，"contour" 或 "contourf"。

get_label( use_latex=False, wrapper='$%s$', )[源代码][源代码]¶

返回用于显示表达式的标签。

参数:

use_latex布尔: 如果为 False，则返回表达式的字符串表示。如果为 True，则返回 latex 表示。
包装器str: 后端可能需要将latex表示用某些字符包裹。默认为 "$%s$"。

返回:

标签str

后端¶

class sympy.plotting.plot.MatplotlibBackend(*series, **kwargs)[源代码][源代码]¶

此类实现了将 Matplotlib 与 SymPy 绘图函数结合使用的功能。

属性:

annotations: 自 1.13 版本弃用.
后端
fill: 自 1.13 版本弃用.
markers: 自 1.13 版本弃用.
rectangles: 自 1.13 版本弃用.

方法

`append`(arg)	将图表系列中的一个元素添加到现有图表中。
`extend`(arg)	添加来自另一个图表的所有系列。
`get_segments`(x, y[, z])	将两个坐标列表转换为线段列表，以用于 Matplotlib 的 `LineCollection`。
`process_series`()	遍历每个 `Plot` 对象，并进一步调用 _process_series()。

关闭
保存
显示

static get_segments(x, y, z=None)[源代码][源代码]¶

将两个坐标列表转换为线段列表，以用于 Matplotlib 的 LineCollection。

参数:

x列表: x坐标列表
y列表: y坐标列表
z列表: 三维线条的z坐标列表。

process_series()[源代码][源代码]¶: 遍历每个 Plot 对象，并进一步调用 _process_series()。

class sympy.plotting.plot.TextBackend(*args, **kwargs)[源代码][源代码]¶

属性:

annotations: 自 1.13 版本弃用.
后端
fill: 自 1.13 版本弃用.
markers: 自 1.13 版本弃用.
rectangles: 自 1.13 版本弃用.

方法

`append`(arg)	将图表系列中的一个元素添加到现有图表中。
`extend`(arg)	添加来自另一个图表的所有系列。

关闭
保存
显示

Pyglet 绘图¶

这是使用 pyglet 的旧绘图模块的文档。该模块有一些限制，并且不再积极开发。作为替代方案，您可以查看新的绘图模块。

pyglet 绘图模块可以进行漂亮的 2D 和 3D 绘图，这些绘图可以通过控制台命令以及键盘和鼠标进行控制，唯一的依赖是 pyglet。

以下是最简单的用法：

>>> from sympy import var
>>> from sympy.plotting.pygletplot import PygletPlot as Plot
>>> var('x y z')
>>> Plot(x*y**3-y*x**3)

要查看许多绘图示例，请参见 examples/pyglet_plotting.py 并在交互模式下运行它（python -i plotting.py）:

$ python -i examples/pyglet_plotting.py

例如输入 example(7) 或 example(11)。

另请参阅绘图模块 wiki 页面以获取截图。

绘图窗口控制¶

相机	键
灵敏度修饰符	SHIFT
缩放	R 和 F, Page Up 和 Page Down, Numpad + 和 -
旋转视图 X,Y 轴	方向键, A,S,D,W, 数字键盘 4,6,8,2
旋转视图 Z 轴	Q 和 E，小键盘 7 和 9
旋转 Z 轴坐标	Z 和 C，小键盘 1 和 3
查看 XY	F1
查看 XZ	F2
查看 YZ	F3
视图视角	F4
重置	X, 数字键盘 5

Axes	键
切换可见	F5
切换颜色	F6

窗口	键
关闭	ESCAPE
截图	F8

鼠标可以分别通过拖动左键、中键和右键来进行旋转、缩放和平移。

坐标模式¶

Plot 支持多种曲线坐标模式，并且它们对于每个绘制的函数都是独立的。你可以使用 ‘mode’ 命名参数显式指定坐标模式，但对于笛卡尔或参数化绘图，它可以自动确定，因此只需为极坐标、柱坐标和球坐标模式指定。

具体来说，Plot(函数参数) 和 Plot.__setitem__(i, 函数参数)``（通过在 ``Plot 实例上使用数组索引语法访问）将根据您提供的函数数量来解释您的参数：如果您提供一个函数，则解释为笛卡尔图；如果您提供两个或三个函数，则解释为参数图。类似地，如果使用一个变量，参数将被解释为曲线；如果使用两个变量，则被解释为曲面。

支持的模式名称按变量数量：

1 (曲线): 参数式, 笛卡尔式, 极坐标式
2 (曲面): 参数化, 笛卡尔, 柱面, 球面

>>> Plot(1, 'mode=spherical; color=zfade4')

请注意，函数参数以 "key1=value1; key2 = value2" 形式的选项字符串给出（空格会被截断）。直接传递给 plot 的关键字参数应用于绘图本身。

指定变量的区间¶

变量区间的基本格式是 [var, min, max, steps]。然而，语法非常灵活，未指定的参数会从当前坐标模式的默认值中获取：

>>> Plot(x**2) # implies [x,-5,5,100]
>>> Plot(x**2, [], []) # [x,-1,1,40], [y,-1,1,40]
>>> Plot(x**2-y**2, [100], [100]) # [x,-1,1,100], [y,-1,1,100]
>>> Plot(x**2, [x,-13,13,100])
>>> Plot(x**2, [-13,13]) # [x,-13,13,100]
>>> Plot(x**2, [x,-13,13]) # [x,-13,13,100]
>>> Plot(1*x, [], [x], 'mode=cylindrical') # [unbound_theta,0,2*Pi,40], [x,-1,1,20]

使用交互式界面¶

>>> p = Plot(visible=False)
>>> f = x**2
>>> p[1] = f
>>> p[2] = f.diff(x)
>>> p[3] = f.diff(x).diff(x)
>>> p
[1]: x**2, 'mode=cartesian'
[2]: 2*x, 'mode=cartesian'
[3]: 2, 'mode=cartesian'
>>> p.show()
>>> p.clear()
>>> p
<blank plot>
>>> p[1] =  x**2+y**2
>>> p[1].style = 'solid'
>>> p[2] = -x**2-y**2
>>> p[2].style = 'wireframe'
>>> p[1].color = z, (0.4,0.4,0.9), (0.9,0.4,0.4)
>>> p[1].style = 'both'
>>> p[2].style = 'both'
>>> p.close()

使用自定义颜色函数¶

以下代码绘制了一个鞍点，并根据其梯度的大小进行着色：

>>> fz = x**2-y**2
>>> Fx, Fy, Fz = fz.diff(x), fz.diff(y), 0
>>> p[1] = fz, 'style=solid'
>>> p[1].color = (Fx**2 + Fy**2 + Fz**2)**(0.5)

着色算法的工作原理如下：

评估曲线或曲面上的颜色函数。
找到每个分量的最小值和最大值。
将每个组件缩放到颜色渐变。

当未明确指定时，默认的颜色渐变是 $f(0.0)=(0.4,0.4,0.4) ightarrow f(1.0)=(0.9,0.9,0.9)$。在我们的例子中，所有内容都是灰度级的，因为我们为每个颜色分量均匀地应用了默认的颜色渐变。当以这种方式定义颜色方案时，您可能还需要提供一个颜色渐变：

>>> p[1].color = (Fx**2 + Fy**2 + Fz**2)**(0.5), (0.1,0.1,0.9), (0.9,0.1,0.1)

这里有一个四步的颜色渐变：

>>> gradient = [ 0.0, (0.1,0.1,0.9), 0.3, (0.1,0.9,0.1),
...              0.7, (0.9,0.9,0.1), 1.0, (1.0,0.0,0.0) ]
>>> p[1].color = (Fx**2 + Fy**2 + Fz**2)**(0.5), gradient

指定颜色方案的另一种方法是分别为每个组件 r、g、b 提供一个单独的函数。使用这种语法，默认的颜色方案定义如下：

>>> p[1].color = z,y,x, (0.4,0.4,0.4), (0.9,0.9,0.9)

这映射 z->红色，y->绿色，和 x->蓝色。在某些情况下，您可能更喜欢使用以下替代语法：

>>> p[1].color = z,(0.4,0.9), y,(0.4,0.9), x,(0.4,0.9)

你仍然可以在三函数配色方案中使用多步渐变。

绘制几何实体¶

绘图模块能够绘制一些二维几何实体，如直线、圆和椭圆。以下示例绘制了一个以原点为中心、半径为2个单位的圆。:

>>> from sympy import *
>>> x,y = symbols('x y')
>>> plot_implicit(Eq(x**2+y**2, 4))

同样地，plot_implicit() 可以用来绘制任何从其隐式方程表示的二维几何结构。

绘制多边形（Polygon, RegularPolygon, Triangle）不直接支持。

使用ASCII艺术绘图¶

sympy.plotting.textplot.textplot(expr, a, b, W=55, H=21)[源代码][源代码]¶

打印 SymPy 表达式 ‘expr’（该表达式应包含一个符号，例如 x 或其他符号）在区间 [a, b] 上的粗略 ASCII 艺术图。

示例

>>> from sympy import Symbol, sin
>>> from sympy.plotting import textplot
>>> t = Symbol('t')
>>> textplot(sin(t)*t, 0, 15)
 14 |                                                  ...
    |                                                     .
    |                                                 .
    |                                                      .
    |                                                .
    |                            ...
    |                           /   .               .
    |                          /
    |                         /      .
    |                        .        .            .
1.5 |----.......--------------------------------------------
    |....       \           .          .
    |            \         /                      .
    |             ..      /             .
    |               \    /                       .
    |                ....
    |                                    .
    |                                     .     .
    |
    |                                      .   .
-11 |_______________________________________________________
     0                          7.5                        15