背景#

什么是时间序列预测？#

一般来说，预测意味着对未来事件做出预测。微不足道的是，在时间序列预测中，我们希望预测给定时间序列的未来值。

例如，在电力生产中，需求和供应保持平衡非常重要。因此，生产者预测消费者对电力的需求，并相应地规划生产能力。换句话说，生产者依赖于对消费者电力需求的准确时间序列预测，以产生足够的供应。

在预测中，隐含假设是影响时间序列值的过去可观察行为将继续在未来存在。以电力示例为例：人们通常在夜间消耗的能源少于白天，在晚上主要观看电视，并在夏天炎热时使用空调。

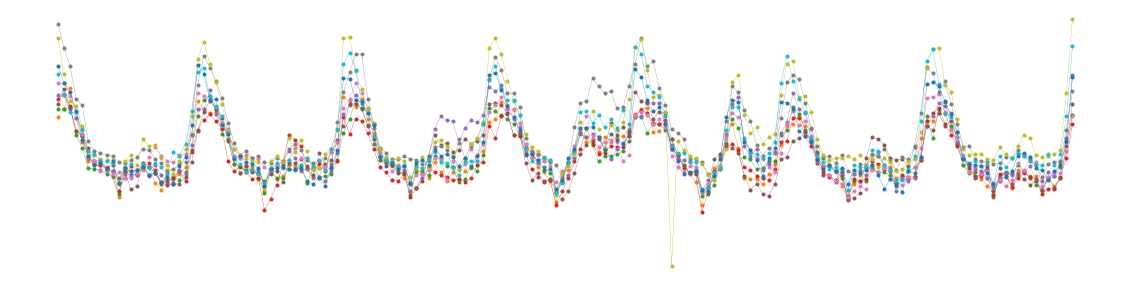
叠加的十周数据 – electricity 数据集。#

自然地，预测不可预测的事情是不可能的。例如，在2019年，当试图预测2020年的旅行需求时，几乎不可能考虑到由于Covid-19疫情而可能出现的旅行限制。

因此，预测的前提是生成时间序列值的基础因素在未来不会发生根本性的变化。这是一个用来预测普通情况而非惊人事件的工具。

换个角度来看：模型实际上是被训练来预测过去的，只有我们才使用模型进行未来的预测。

我们称我们想要预测的时间序列为 target 时间序列。过去的目标值是模型可以用来进行准确预测的最重要的信息。

此外，模型可以使用特征，即对目标值有影响的附加值。我们区分“静态”和“动态”特征。

动态特征可以在每个时间点上有所不同。例如，这可能是产品的价格，也可以是更一般的信息，例如外部空气温度。从内部来看，我们为时间序列的年龄或今天是星期几等内容生成动态特征。

重要

大多数模型在进行预测时需要在未来的时间范围内提供动态特征。

相对而言，静态特征独立于时间描述时间序列。如果我们想预测不同商店中的不同产品，可以使用静态特征来标记每个时间序列，以包含商店和产品标识符。

我们进一步区分分类特征和连续（实数）特征。这个想法是，在连续特征中，数字本身具有意义，例如在使用价格作为特征时。另一方面，分类特征没有相同的属性：商店 0、 1 和 2 是不同的实体，没有“更高商店”的概念。

GluonTS中的一个核心思想是我们并不生成简单的值作为预测，而实际上是预测分布。

一种直观的看法是想象预测一个时间序列100次，这会返回100个不同的时间序列样本，这些样本形成一个围绕它们的分布——只不过我们可以直接发出这些分布，然后从中抽取样本。

分布的好处在于它们提供了一系列可能的值。想象一下，作为一名餐厅老板，想知道应该购买多少食材；如果我们买得太少，就无法满足顾客的需求，但买得太多则会造成浪费。因此，当我们预测需求时，如果模型能够告诉我们，可能有大约50道菜的需求，但不太可能超过60道，那将是非常有价值的。

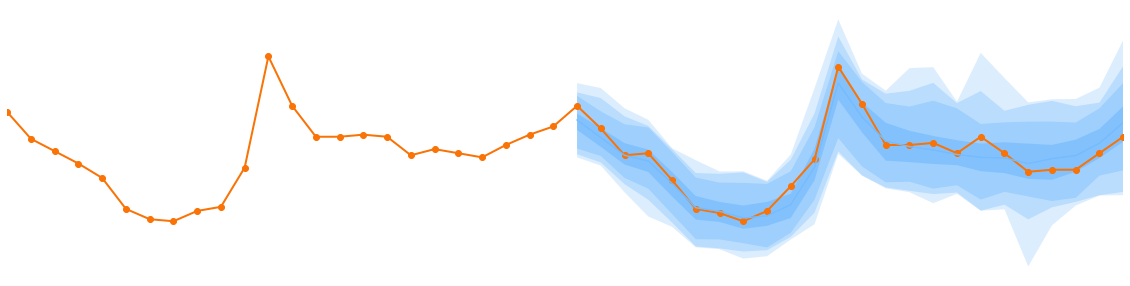
预测24小时，显示 p50, p90, p95, p98 预测区间。#

注意

预测的分布并不权威：预测的第90百分位数并不意味着只有10%的实际值会更高，而是模型对这一线的位置的猜测。

在GluonTS中，我们使用局部模型和全局模型的概念。

局部模型适合于单个时间序列，并用于对该时间序列进行预测，而全局模型是在多个时间序列上训练的，单个全局模型用于对数据集中的所有时间序列进行预测。

训练一个全局模型可能需要很长时间：长达数小时，但有时甚至数天。因此，将模型训练作为预测请求的一部分是不可行的，训练过程作为一个单独的“离线”步骤进行。相比之下，拟合一个局部模型通常要快得多，并作为预测的一部分“在线”进行。

在GluonTS中，局部模型可以直接作为预测器使用，而全局模型作为估计器提供，需要先进行训练。