面向对象建模#

多个相似类型的对象往往具有共同的逻辑和数据定义。 手动逐个建模这些对象不是一个好主意，因为最终你会得到多个相同定义的副本，这些副本难以维护且容易出错。

modelx支持继承机制，使您能够将多个对象共有的部分仅定义一次作为基础对象的一部分，并通过从基础对象继承并仅定义对象特有的部分来建模每个对象。 通过充分利用继承，您可以将具有相似特征的多个对象组织成继承树，最大限度地减少重复公式，保持模型的条理性和透明度，同时维护模型的完整性。

面向对象编程中的继承#

你可能听说过面向对象编程(OOP)。 OOP是一种编程范式，大多数现代编程语言如Python和C++都支持OOP。 这些语言包含了强大的机制，比如继承， 可以优雅地建模复杂对象。 OOP语言中的继承极大地提高了代码的可重用性和可扩展性。

modelx的灵感来源于面向对象编程(OOP)，并实现了类似于OOP的继承机制。 然而，虽然大多数流行的面向对象编程语言使用基于类的继承， modelx则采用基于原型的继承。

以Python为例，它使用基于类的继承机制。Python允许您定义类，而对象则是这些类的实例。在Python中，继承关系是通过类来定义的。

在modelx中，没有等效的类概念，继承关系是通过Space对象之间定义的。一个空间对象继承自另一个空间对象，目的是将后者作为原型使用。

modelx中的继承机制如何运作#

当您定义一个空间（我们称之为A）作为另一个空间（我们称之为B）的基空间时，就建立了继承关系。在这种情况下，A被称为B的基空间，而B被称为A的子空间。当B继承自A时，A中包含的所有单元格、引用和空间的副本都会自动在B中创建。这种自动复制的过程称为派生。例如，假设A有一个子单元格foo和一个子引用bar。如图所示，另一组foo和bar会在B中被派生出来。A和B之间的连线，在A一侧带有空心三角形箭头，表示B继承自A。

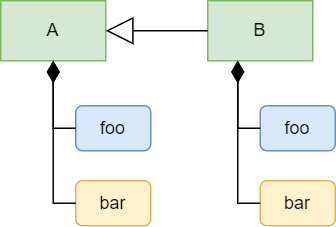
../_images/SingleInheritance.png

最初，foo的公式和B中bar的值是从A中复制而来的，但你可以更新B中foo的公式和bar的值。这种更新派生对象的操作称为覆盖。你还可以在B中添加一个新的子对象，例如一个名为baz的新单元格。

../_images/SingleInheritance2.png

可调利率抵押贷款示例#

让我们通过建模一个简单的金融产品来学习如何实现继承。

在本教程的前面部分，一个简单的固定利率抵押贷款被建模为Fixed空间。 假设我们还想建模一个可调利率抵押贷款。 为简化起见，我们假设可调利率抵押贷款与固定利率抵押贷款具有相同的贷款期限和本金。 在本例中，设贷款期限为10年，本金为100,000。

在前5年，可调利率抵押贷款的利率固定为2%，但从第6年开始，利率每年更新直至贷款期结束。 假设预期利率如下：

年份

1

2

3

4

5

6

7

8

9

10

利率

2%

2%

2%

2%

2%

4%

5%

6%

5%

4%

请注意，贷款初始时无法确定前5年后的适用利率，因为该利率并非预先固定。因此，如果我们正在模拟一笔在未来某个时间点偿还的贷款，上述利率表实际上是一个假设或情景。

我们希望将可调整利率抵押贷款建模为Adjustable空间。 由于Fixed和Adjustable都属于抵押贷款，并且预期会共享部分公式和值的定义，因此可以利用继承机制。 我们创建一个基础空间BaseMortgage，并在其中定义Fixed和Adjustable共有的单元格和引用。 Fixed和Adjustable继承自BaseMortgage，同时我们会重写从BaseMortgage继承的部分派生对象以体现它们自身的特性。下图展示了这些空间之间的关系。

../_images/Inheritance.png

为了识别这两种抵押贷款之间的共性，让我们逐一回顾前面示例中的Fixed内容，并思考是否需要以及如何更新它们。

  • Term 是一个整数，表示贷款期限的年数。我们上面假设固定利率和可调利率抵押贷款的期限相同。

  • Principal 表示初始贷款余额，作为输入给出。我们上面假设固定利率和可调利率抵押贷款的本金金额相同。

  • Rate 是一个适用于固定利率抵押贷款整个生命周期的恒定利率。由于Adjustable的利率会定期调整，Adjustable的Rate应与Fixed有不同的定义。可调利率可以定义为按贷款期限索引的dict。

  • Payment 表示定期偿还贷款的付款金额。对于Fixed类型，Payment是根据Principal、Term和Rate计算出的固定金额。而Adjustable类型的Payment需要随时间变化，因为它会定期根据利率变动重新计算。我们将重新定义Payment的公式，使其具有时间依赖性，并同时适用于Fixed和Adjustable类型。

  • 与其直接从Payment引用Rate，不如通过带有时间索引的新单元格间接引用Rate， 因为固定利率和可调利率可以用相同的方式通过时间索引来引用。我们将这些单元格命名为IntRate。

  • Balance 以时间索引 t 为索引，表示在时间 t 时的贷款剩余余额。 Balance 的公式通过递归计算从前一个余额得出时间 t 时的贷款余额。 初始余额从 Principal 输入，并引用 Rate 来计算利息增长。 通过将 Rate 替换为 IntRate(t)，该公式在 Fixed 和 Adjustable 之间变得通用。

以下表格总结了每个空间的内容应如何定义。

目录

BaseMortgage

Fixed

可调节

Term

10

继承自 BaseMortgage

继承自 BaseMortgage

Principal

100000

继承自 BaseMortgage

继承自 BaseMortgage

Rate

待定义

0.03

一个 dict 对象

Payment(t)

共享公式

继承自 BaseMortgage

继承自 BaseMortgage

IntRate(t)

待定义

独特公式

独特公式

Balance(t)

共享公式

继承自 BaseMortgage

继承自 BaseMortgage

你可能已经注意到，除了创建BaseMortgage之外， 还可以通过继承Fixed来建模Adjustable。 虽然这在技术上是可行的，但这不是一个好的设计，因为 可调利率抵押贷款并不是固定利率抵押贷款的一种特殊形式。 良好的实践是确保继承关系始终代表"是一种"的关系。

建模继承#

我们从之前的示例中的Mortgage模型开始，但如果您愿意，也可以从头开始：

>>> import modelx as mx

>>> model = mx.read_model("Mortgage")

让我们使用Fixed空间作为基础空间。将其重命名为BaseMortgage：

>>> model.Fixed.rename('BaseMortgage')

>>> model.BaseMortgage
<UserSpace Mortgage.BaseMortgage>

现在将10设置为Term，这是一个在子空间之间共享的常量：

>>> model.BaseMortgage.Term = 10

现在让我们通过继承BaseMortgage在模型下创建Fixed。 您可以通过将BaseMortgage传递给模型的new_space方法的bases参数来实现：

>>> model.new_space('Fixed', bases=model.BaseMortgage)

同样地，通过继承BaseMortgage来创建Adjustable：

>>> model.new_space('Adjustable', bases=model.BaseMortgage)

你也可以使用add_bases方法在现有空间之间定义继承关系。除了通过调用带有bases参数的new_space之外，你也可以先不带bases参数调用new_space来创建Fixed和Adjustable，之后再对Fixed和Adjustable调用add_bases方法，将BaseMortgage设置为它们的基空间：

>>> model.new_space('Fixed')

>>> model.new_space('Adjustable')

>>> model.Fixed.add_bases(model.Mortgage)

>>> model.Adjustable.add_bases(model.Mortgage)

接下来，我们为Adjustable按期限设置利率，使用dict格式。 请注意索引从0开始，因此第N个利率对应的键是(N-1):

>>> model.Adjustable.Rate = {
...     0: 0.02,
...     1: 0.02,
...     2: 0.02,
...     3: 0.02,
...     4: 0.02,
...     5: 0.04,
...     6: 0.05,
...     7: 0.06,
...     8: 0.05,
...     9: 0.04
... }

你也可以将0.03赋值给Fixed中的Rate，尽管该值是继承的：

>>> model.Fixed.Rate = 0.03

为了在Fixed和Adjustable中以相同方式引用Rate，我们创建了一个以t为索引的单元格IntRate。首先在BaseMortgage中创建IntRate，并将其公式定义为抛出NotImplementedError，表示需要在子空间中定义。有几种方法可以定义IntRate的公式。这里我们通过先定义一个Python函数，然后将其赋值给InRate的公式来实现：

>>> IntRate = model.BaseMortgage.new_cells('IntRate')

>>> def temp(t): # the name of the function can be anything.
        raise NoteImplementedError

>>> IntRate.formula = temp

>>> IntRate.formula
def IntRate(t):
    raise NoteImplementedError

然后在 Fixed 和 Adjustable 中重写 IntRate，使其引用它们自己的 Rate：

>>> model.Fixed.IntRate.formula = lambda t: Rate

>>> model.Adjustable.IntRate.formula = lambda t: Rate[t]

>>> model.Adjustable.IntRate[5]
0.04

接下来，我们将在BaseMortgage中定义Payment，这样基础空间中的Payment定义就可以被继承，并在Fixed和Adjustable中无需修改地使用。

更新前的公式在BaseMortgage中应如下所示，因为我们是从前面示例中的Fixed形式开发而来的：

def Payment():
    return Principal * Rate * (1+Rate)**Term / ((1+Rate)**Term - 1)

上述公式精确地表示了以下数学表达式，这是一个已知的公式，用于计算在期限`年数`内偿还债务所需的等额年度支付金额，其中利息按``利率`每年累积。

\[Payment = Principal\cdot\frac{Rate(1+Rate)^{Term}}{(1+Rate)^{Term}-1}\]

为了使公式适用于Adjustable，我们需要进行以下更改。

  • 用 t 参数化 Payment

  • 将 Rate 替换为 IntRate(t-1)

  • 将 Principal 替换为 Balance(t-1)

  • 将 Term 替换为 Term - t + 1

表达式现在看起来如下所示：

Balance(t-1) * IntRate(t-1) * (1 + IntRate(t-1))** (Term - t + 1) / ((1 + IntRate(t-1))** (Term - t + 1) - 1)

对应的数学表达式如下：

\[Payment(t) = Balance(t-1)\cdot\frac{IntRate(t)(1+IntRate(t))^{Term-t+1}}{(1+IntRate(t))^{Term-t+1}-1}\]

你可能会好奇为什么Payment(t)引用的是Balance(t-1)和IntRate(t-1)， 而不是Balance(t)和IntRate(t)。 你可能还会疑惑为什么剩余期限不是Term - t而是Term - t + 1。

下图展示了Payment(6)的计算方式。 Payment(6)是在t=5时计算的，假设IntRate(5)将在剩余贷款期限内持续适用，那么支付该金额（5年）将能偿还Balance(5)及其按IntRate(5)计算的应计利息。

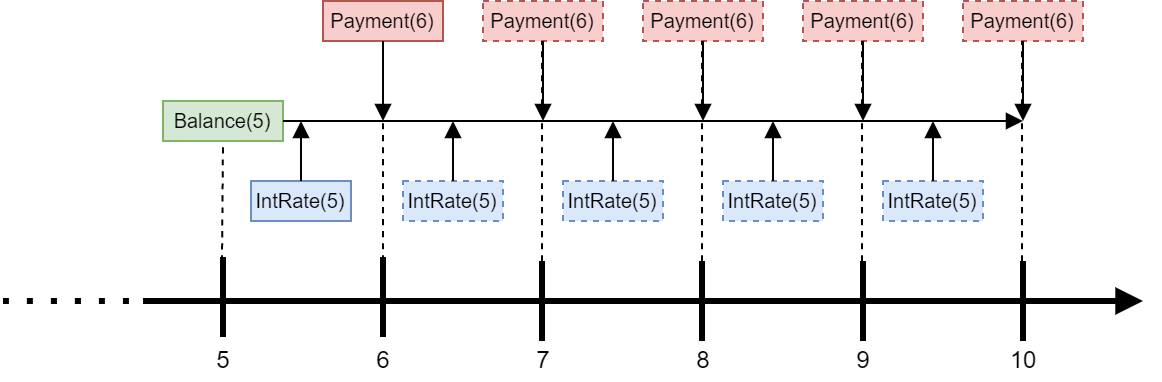
../_images/PaymentAt6.png

实际上，利率每年都会更新，因此一年后当t=6时， IntRate(6)可能与IntRate(5)不同。在这种情况下，Payment(7)会被重新计算， 使得更新后的金额能够偿还Balance(6)以及剩余贷款期限内按IntRate(6)计算的利息。

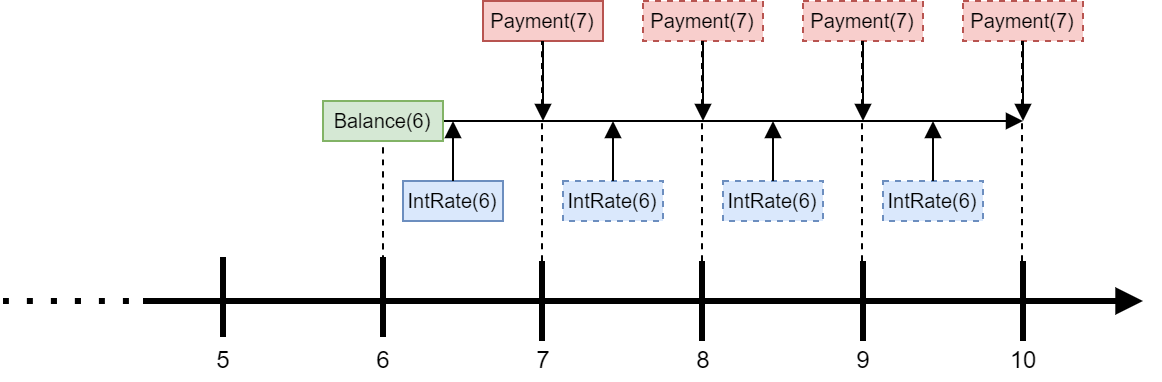
../_images/PaymentAt7.png

注意上面的Payment公式同样适用于Fixed，因为如果利率不变，在贷款期间内公式Payment对t会返回相同的值。因此我们在BaseMortgage中定义了Payment。下面的代码更新了BaseMortgage中的Payment。r和u的定义是为了使表达式更简洁：

>>> def temp(t):
...     r = IntRate(t-1)
...     u = Term - t + 1
...     return Balance(t-1) * r * (1 + r)**u / ((1 + r)**u - 1)

>>> model.BaseMort.Payment.formula = temp

我们需要再更新一个单元格。Balance在BaseMortgage中定义如下：

>>> model.Mortgage.Balance.formula
def Balance(t):

    if t > 0:
        return Balance(t-1) * (1+Rate) - Payment
    else:
        return Principal

公式应分别引用IntRate(t-1)和Payment(t)，而非Rate和Payment：

>>> def temp(t):
...     if t > 0:
...         return Balance(t-1) * (1 + IntRate(t-1)) - Payment(t)
...     else:
...         return Principal

>>> model.BaseMortgage.Balance.formula = temp

检查结果#

现在我们已经完成了所有必要的修改， 让我们来查看结果。 下方可调整的付款以dict形式输出。 正如预期的那样，付款在前5年后增加， 因为t=5时的利率高于之前。 随后付款每年变化，反映出利率的变动：

>>> {t: model.Adjustable.Payment(t) for t in range(1 ,11)}
{1: 11132.652786531637,
 2: 11132.65278653164,
 3: 11132.652786531638,
 4: 11132.652786531644,
 5: 11132.65278653164,
 6: 11786.927741021387,
 7: 12065.96444749335,
 8: 12292.72989621633,
 9: 12120.72411143264,
 10: 12005.288643704713}

>>> model.Adjustable.Payment.series.plot()
../_images/AdjustablePaymentPlot.png

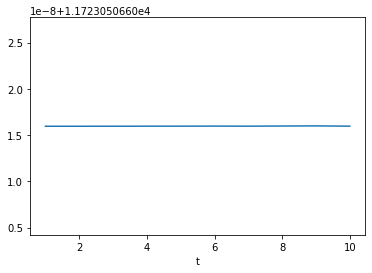
为了与可调整还款进行比较，我们也输出并绘制固定还款。如下所示，尽管每年都会通过与Adjustable相同的公式重新计算还款额，但固定还款在整个贷款期间保持不变：

>>> {t: model.Fixed.Payment(t) for t in range(1 ,11)}
{1: 11723.050660515952,
 2: 11723.050660515952,
 3: 11723.050660515953,
 4: 11723.050660515959,
 5: 11723.05066051596,
 6: 11723.050660515968,
 7: 11723.05066051596,
 8: 11723.050660515977,
 9: 11723.05066051599,
 10: 11723.05066051596}

>>> model.Fixed.Payment.series.plot()
../_images/FixedPaymentPlot.png

以下是Adjustable.Balance的输出结果。 可以看到余额实际上在t=0时已全部偿还：

>>> {t: model.Adjustable.Balance(t) for t in range(0 ,11)}
{0: 100000,
 1: 90867.34721346837,
 2: 81552.0413712061,
 3: 72050.42941209857,
 4: 62358.78521380889,
 5: 52473.30813155344,
 6: 42785.31271579419,
 7: 32858.613904090555,
 8: 22537.40084211966,
 9: 11543.546772793003,
 10: 1.0913936421275139e-11}

>>> model.Adjustable.Balance.series.plot()
../_images/AdjustableBalancePlot.png