TSB模型


# 此单元格将不会被渲染，但用于隐藏警告并限制显示的行数。

import warnings
warnings.filterwarnings("ignore")

import logging
logging.getLogger('statsforecast').setLevel(logging.ERROR)

import pandas as pd
pd.set_option('display.max_rows', 6)

使用TSB模型和Statsforecast的逐步指南。

在这个演示中，我们将熟悉主要的StatsForecast类以及一些相关的方法，例如StatsForecast.plot、StatsForecast.forecast和StatsForecast.cross_validation等。

介绍

Teunter-Syntetos-Babai (TSB) 模型是用于库存管理和时间序列需求预测领域的一种模型。它由 Teunter、Syntetos 和 Babai 于 2001 年提出，是 Croston 需求预测模型的扩展。

TSB 模型专门用于预测具有间歇性需求特征的产品需求，即经历需求期后又有非需求期的产品。它旨在处理具有大量零值和非零观测间隔变化的时间序列数据。

TSB 模型基于两个主要组成部分：水平模型和间隔模型。水平模型在需求发生时估计需求水平，而间隔模型则估计需求发生之间的间隔。这两个组成部分结合在一起生成对未来需求的准确预测。

TSB 模型已被证明在间歇性需求预测中有效，并在各个工业部门得到广泛应用。然而，重要的是要注意还有其他模型和方法可用于需求预测，选择适当的模型将依赖于数据的具体特征以及应用上下文。

TSB 模型

TSB（Teunter, Syntetos 和 Babai）是一种2011年提出的新方法，该方法通过每个周期更新的需求概率替代需求间隔。这是因为Croston方法仅在需求发生时更新，而在现实生活中，存在许多零需求的情况，因此，预测结果将不适合估算因过时信息而产生的滞销风险。

在TSB方法中，\(D_t\)表示时期\(t\)的需求发生指标，因此：

如果 \(D_t=0\)，则

\[Z'_t=Z'_{t-1}\]

\[D_t=D'_{t-1}+\beta (0- D'_{t-1})\]

否则 \[Z'_t=Z'_{t-1}+\alpha(Z_t - Z'_{t-2})\]

\[D'_t=D'_{t-1}+\beta(1-D'_{t-1})\]

因此，预测由以下公式给出：

\[Y'_t=D'_t \cdot Z'_t\]

其中

\(Y'_t:\) 每期平均需求
\(Z_t:\) 第\(t\)期的实际需求
\(Z'_t:\) 两次正需求之间的时间
\(D'_t:\) 对第\(t\)期末需求发生的估计概率
\(\alpha, \beta:\) 平滑常数，\(0 \leq \alpha, \beta \leq 1\)

TSB一般属性

Teunter-Syntetos-Babai（TSB）时间序列模型具有以下属性：

间歇性需求建模：TSB模型专门设计用于预测间歇性需求，这种需求特征是由非需求期和需求期交替组成的。该模型有效地处理了这种需求特征。
水平和间隔组件：TSB模型基于两个主要组件：水平模型和间隔模型。水平模型在需求发生时估计需求水平，而间隔模型则估计需求发生之间的间隔。
处理大量零的数据：TSB模型能够有效处理具有大量零的时间序列数据，而这样的数据在间歇性需求中很常见。该模型在预测过程中正确考虑了这些零值。
指数平滑：TSB模型使用指数平滑方法来估计需求水平和发生之间的间隔。指数平滑是时间序列预测中广泛使用的一种技术。
置信区间估计：TSB模型为生成的预测提供置信区间估计。这允许我们得到与预测相关的不确定性度量，从而促进决策。
简便和易于实施：与其他更复杂的方法相比，TSB模型相对简单且易于实施。它不需要对需求分布做出复杂的假设，并且可以以实际的方式应用。

这些是Teunter-Syntetos-Babai模型在时间序列和间歇性需求预测上下文中的一些基本属性。

加载库和数据

Tip

需要使用Statsforecast。要安装，请参见说明。

接下来，我们导入绘图库并配置绘图样式。

import matplotlib.pyplot as plt
import seaborn as sns
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
plt.style.use('grayscale') # 五三八 灰度 经典
plt.rcParams['lines.linewidth'] = 1.5
dark_style = {
    'figure.facecolor': '#008080',  # #212946
    'axes.facecolor': '#008080',
    'savefig.facecolor': '#008080',
    'axes.grid': True,
    'axes.grid.which': 'both',
    'axes.spines.left': False,
    'axes.spines.right': False,
    'axes.spines.top': False,
    'axes.spines.bottom': False,
    'grid.color': '#000000',  #2A3459
    'grid.linewidth': '1',
    'text.color': '0.9',
    'axes.labelcolor': '0.9',
    'xtick.color': '0.9',
    'ytick.color': '0.9',
    'font.size': 12 }
plt.rcParams.update(dark_style)


from pylab import rcParams
rcParams['figure.figsize'] = (18,7)

import pandas as pd

df=pd.read_csv("https://raw.githubusercontent.com/Naren8520/Serie-de-tiempo-con-Machine-Learning/main/Data/intermittend_demand2")
df.head()

	date	sales
0	2022-01-01 00:00:00	0
1	2022-01-01 01:00:00	10
2	2022-01-01 02:00:00	0
3	2022-01-01 03:00:00	0
4	2022-01-01 04:00:00	100

StatsForecast 的输入始终是一个长格式的数据框，包含三列：unique_id、ds 和 y：

unique_id（字符串、整数或类别）表示系列的标识符。
ds（日期戳）列应为 Pandas 期望的格式，理想情况下日期应为 YYYY-MM-DD，时间戳应为 YYYY-MM-DD HH:MM:SS。
y（数值）表示我们希望预测的测量值。

df["unique_id"]="1"
df.columns=["ds", "y", "unique_id"]
df.head()

	ds	y	unique_id
0	2022-01-01 00:00:00	0	1
1	2022-01-01 01:00:00	10	1
2	2022-01-01 02:00:00	0	1
3	2022-01-01 03:00:00	0	1
4	2022-01-01 04:00:00	100	1

print(df.dtypes)

ds           object
y             int64
unique_id    object
dtype: object

我们可以看到我们的时间变量 (ds) 是以对象格式表示的，我们需要将其转换为日期格式。

df["ds"] = pd.to_datetime(df["ds"])

使用 plot 方法探索数据

使用 StatsForecast 类中的 plot 方法绘制一些序列。该方法从数据集中打印随机序列，对于基本的探索性数据分析非常有用。

from statsforecast import StatsForecast

StatsForecast.plot(df)

自相关图

自相关（ACF）和偏自相关（PACF）图是分析时间序列的统计工具。ACF 图显示了时间序列值与其滞后值之间的相关性，而 PACF 图则显示了时间序列值与其滞后值之间的相关性，在此之前已去除了前面滞后值的影响。

ACF 和 PACF 图可以用来识别时间序列的结构，这在选择适合时间序列的模型时非常有帮助。例如，如果 ACF 图显示出重复的峰谷模式，这表明时间序列是平稳的，意味着它在时间上具有相同的统计特性。如果 PACF 图显示出快速减小的尖峰模式，这表明时间序列是可逆的，意味着可以逆转以获得平稳的时间序列。

ACF 和 PACF 图的重要性在于它们能够帮助分析师更好地理解时间序列的结构。这种理解有助于选择适合时间序列的模型，从而提高对未来时间序列值的预测能力。

要分析 ACF 和 PACF 图：

寻找图表中的模式。常见的模式包括重复的峰和谷、锯齿形模式和平台模式。
比较 ACF 和 PACF 图。PACF 图通常比 ACF 图具有更少的尖峰。
考虑时间序列的长度。较长时间序列的 ACF 和 PACF 图会有更多的尖峰。
使用置信区间。ACF 和 PACF 图还显示了自相关值的置信区间。如果某个自相关值在置信区间之外，通常是显著的。

fig, axs = plt.subplots(nrows=1, ncols=2)

plot_acf(df["y"],  lags=30, ax=axs[0],color="fuchsia")
axs[0].set_title("Autocorrelation");

plot_pacf(df["y"],  lags=30, ax=axs[1],color="lime")
axs[1].set_title('Partial Autocorrelation')

plt.show();

时间序列的分解

如何分解时间序列以及原因是什么？

在时间序列分析中，为了预测新的数值，了解过去的数据是非常重要的。更正式地说，我们可以说了解数值随时间所遵循的模式是非常重要的。导致我们的预测值朝错误方向发展的原因可能有很多。基本上，一个时间序列由四个组成部分构成。这些组成部分的变化导致时间序列模式的变化。这些组成部分是：

水平（Level）： 这是平均随时间变化的主要值。
趋势（Trend）： 趋势是导致时间序列中出现上升或下降模式的值。
季节性（Seasonality）： 这是时间序列中短时间内发生的周期性事件，导致时间序列中出现短期的上升或下降模式。
残差/噪声（Residual/Noise）： 这是时间序列中的随机变化。

随着时间的推移，这些组件的组合导致了时间序列的形成。大多数时间序列包含水平和噪声/残差，而趋势或季节性是可选值。

如果季节性和趋势是时间序列的一部分，那么它们将对预测值产生影响。因为预测的时间序列的模式可能与之前的时间序列不同。

时间序列中组件的组合可以分为两种类型： * 加性（Additive） * 乘性（Multiplicative）

加性时间序列

如果时间序列的组成部分是相加形成时间序列的，那么该时间序列称为加性时间序列。通过可视化，我们可以说，当时间序列的上升或下降模式在整段序列中相似时，该时间序列是加性的。任何加性时间序列的数学函数可以表示为： \[y(t) = 水平 + 趋势 + 季节性 + 噪声\]

乘性时间序列

如果时间序列的组成部分是相乘形成的，那么该时间序列称为乘性时间序列。通过可视化，如果时间序列随着时间呈现指数增长或下降，那么该时间序列可以被视为乘性时间序列。乘性时间序列的数学函数可以表示为： \[y(t) = 水平 * 趋势 * 季节性 * 噪声\]

from plotly.subplots import make_subplots

from statsmodels.tsa.seasonal import seasonal_decompose
from plotly.subplots import make_subplots
import plotly.graph_objects as go

def plotSeasonalDecompose(
    x,
    model='additive',
    filt=None,
    period=None,
    two_sided=True,
    extrapolate_trend=0,
    title="Seasonal Decomposition"):

    result = seasonal_decompose(
            x, model=model, filt=filt, period=period,
            two_sided=two_sided, extrapolate_trend=extrapolate_trend)
    fig = make_subplots(
            rows=4, cols=1,
            subplot_titles=["Observed", "Trend", "Seasonal", "Residuals"])
    for idx, col in enumerate(['observed', 'trend', 'seasonal', 'resid']):
        fig.add_trace(
            go.Scatter(x=result.observed.index, y=getattr(result, col), mode='lines'),
                row=idx+1, col=1,
            )
    return fig

plotSeasonalDecompose(
    df["y"],
    model="additive",
    period=24,
    title="Seasonal Decomposition")

将数据分为训练集和测试集

让我们将数据划分为两个部分： 1. 用于训练我们的TSB模型的数据。 2. 用于测试我们模型的数据。

对于测试数据，我们将使用最后500小时的数据来测试和评估我们模型的性能。

train = df[df.ds<='2023-01-31 19:00:00'] 
test = df[df.ds>'2023-01-31 19:00:00']

train.shape, test.shape

((9500, 3), (500, 3))

现在让我们绘制训练数据和测试数据。

sns.lineplot(train,x="ds", y="y", label="Train", linestyle="--",linewidth=2)
sns.lineplot(test, x="ds", y="y", label="Test", linewidth=2, color="yellow")
plt.title("Store visit");
plt.xlabel("Hours")
plt.show()

`TSB模型`的实现与StatsForecast

要了解有关TSB模型函数的参数的更多信息，您可以查看这里。

alpha_d : float
    需求的平滑参数。
alpha_p : float
    概率的平滑参数。
alias : str
    模型的自定义名称。
prediction_intervals : Optional[ConformalIntervals]
    计算保形预测区间的信息。
    默认情况下，模型将计算本机预测
    区间。

加载库

from statsforecast import StatsForecast
from statsforecast.models import TSB

建立模型

导入并实例化模型。设置参数有时可能比较棘手。Rob Hyndmann 的这篇关于季节周期的文章对于 season_length 非常有帮助。

season_length = 24 # 每小时数据 
horizon = len(test) # 预测数量

models = [TSB(alpha_d=0.8, alpha_p=0.9)]

我们通过使用以下参数实例化一个新的 StatsForecast 对象来拟合模型：

models：一个模型列表。选择您想要的模型并导入它们。

freq: 一个字符串，表示数据的频率。（请参见 pandas 的可用频率。）
n_jobs: n_jobs: int，并行处理使用的作业数量，使用 -1 表示所有核心。
fallback_model: 如果某个模型失败，则使用的备用模型。

所有设置都会传递到构造函数中。然后调用其 fit 方法并传入历史数据框。

sf = StatsForecast(df=df,
                   models=models,
                   freq='H', 
                   n_jobs=-1)

拟合模型

sf.fit()

StatsForecast(models=[TSB])

让我们看看我们的 TSB 模型 的结果。我们可以通过以下指令来观察它：

result=sf.fitted_[0,0].model_
result

{'mean': array([22.443005], dtype=float32)}

预测方法

如果您希望在具有多个系列或模型的生产环境中提高速度，我们建议使用 StatsForecast.forecast 方法，而不是 .fit 和 .predict。

主要区别在于 .forecast 不会存储拟合值，并且在分布式环境中具有很高的可扩展性。

预测方法需要两个参数：预测接下来的 h（时间跨度）和 level。

h (int): 表示向未来预测 h 步。在这种情况下，表示 500 小时之后的预测。

这里的预测对象是一个新的数据框，其中包括一个模型名称列和 y hat 值，以及不确定性区间的列。根据您的计算机，这一步骤应该大约需要 1 分钟。

Y_hat = sf.forecast(horizon)
Y_hat

	ds	TSB
unique_id
1	2023-02-21 16:00:00	22.443005
1	2023-02-21 17:00:00	22.443005
1	2023-02-21 18:00:00	22.443005
...	...	...
1	2023-03-14 09:00:00	22.443005
1	2023-03-14 10:00:00	22.443005
1	2023-03-14 11:00:00	22.443005

500 rows × 2 columns

Y_hat=Y_hat.reset_index()
Y_hat

	unique_id	ds	TSB
0	1	2023-02-21 16:00:00	22.443005
1	1	2023-02-21 17:00:00	22.443005
2	1	2023-02-21 18:00:00	22.443005
...	...	...	...
497	1	2023-03-14 09:00:00	22.443005
498	1	2023-03-14 10:00:00	22.443005
499	1	2023-03-14 11:00:00	22.443005

500 rows × 3 columns

# 将预测值与真实值连接起来
Y_hat1 = pd.concat([df,Y_hat])
Y_hat1

	ds	y	unique_id	TSB
0	2022-01-01 00:00:00	0.0	1	NaN
1	2022-01-01 01:00:00	10.0	1	NaN
2	2022-01-01 02:00:00	0.0	1	NaN
...	...	...	...	...
497	2023-03-14 09:00:00	NaN	1	22.443005
498	2023-03-14 10:00:00	NaN	1	22.443005
499	2023-03-14 11:00:00	NaN	1	22.443005

10500 rows × 4 columns

fig, ax = plt.subplots(1, 1)
plot_df = pd.concat([df, Y_hat1]).set_index('ds')
plot_df['y'].plot(ax=ax, linewidth=2)
plot_df["TSB"].plot(ax=ax, linewidth=2, color="yellow")
ax.set_title(' Forecast', fontsize=22)
ax.set_ylabel("Store visit (Hourly data)", fontsize=20)
ax.set_xlabel('Hours', fontsize=20)
ax.legend(prop={'size': 15})
ax.grid(True)

使用置信区间的预测方法

要生成预测，请使用预测方法。

预测方法需要两个参数：预测下一个 h（表示时间范围）和 level。

h (int): 表示预测向前 h 步。在这种情况下，预见到 500 小时之后。

此处的预测对象是一个新的数据框，其中包含一个模型名称列和 y 估计值列，以及不确定性区间的列。

此步骤应该花费不到 1 秒。

forecast_df = sf.predict(h=horizon) 

forecast_df

	ds	TSB
unique_id
1	2023-02-21 16:00:00	22.443005
1	2023-02-21 17:00:00	22.443005
1	2023-02-21 18:00:00	22.443005
...	...	...
1	2023-03-14 09:00:00	22.443005
1	2023-03-14 10:00:00	22.443005
1	2023-03-14 11:00:00	22.443005

500 rows × 2 columns

我们可以使用pandas函数pd.concat()将预测结果与历史数据合并，然后可以使用此结果进行绘图。

pd.concat([df, forecast_df]).set_index('ds')

	y	unique_id	TSB
ds
2022-01-01 00:00:00	0.0	1	NaN
2022-01-01 01:00:00	10.0	1	NaN
2022-01-01 02:00:00	0.0	1	NaN
...	...	...	...
2023-03-14 09:00:00	NaN	NaN	22.443005
2023-03-14 10:00:00	NaN	NaN	22.443005
2023-03-14 11:00:00	NaN	NaN	22.443005

10500 rows × 3 columns

df_plot= pd.concat([df, forecast_df]).set_index('ds').tail(5000)
df_plot

	y	unique_id	TSB
ds
2022-08-18 04:00:00	0.0	1	NaN
2022-08-18 05:00:00	80.0	1	NaN
2022-08-18 06:00:00	0.0	1	NaN
...	...	...	...
2023-03-14 09:00:00	NaN	NaN	22.443005
2023-03-14 10:00:00	NaN	NaN	22.443005
2023-03-14 11:00:00	NaN	NaN	22.443005

5000 rows × 3 columns

现在让我们可视化我们预测的结果和时间序列的历史数据。

plt.plot(df_plot['y'],label="Actual", linewidth=2.5)
plt.plot(df_plot['TSB'], label="TSB", color="yellow") # '-', '--', '-.', ':',

plt.title("Store visit (Hourly data)");
plt.xlabel("Hourly")
plt.ylabel("Store visit")
plt.legend()
plt.show();

让我们使用Statsforecast中的plot函数绘制相同的图形，如下所示。

sf.plot(df, forecast_df)

交叉验证

在之前的步骤中，我们使用历史数据来预测未来。然而，为了评估其准确性，我们还希望了解模型在过去的表现。为了评估模型在数据上的准确性和稳健性，执行交叉验证。

对于时间序列数据，交叉验证是通过在历史数据上定义滑动窗口并预测其后续时期来完成的。这种形式的交叉验证使我们能够在更广泛的时间实例中更好地估计模型的预测能力，同时保持训练集中的数据连续，这是我们模型所要求的。

下面的图展示了这样一种交叉验证策略：

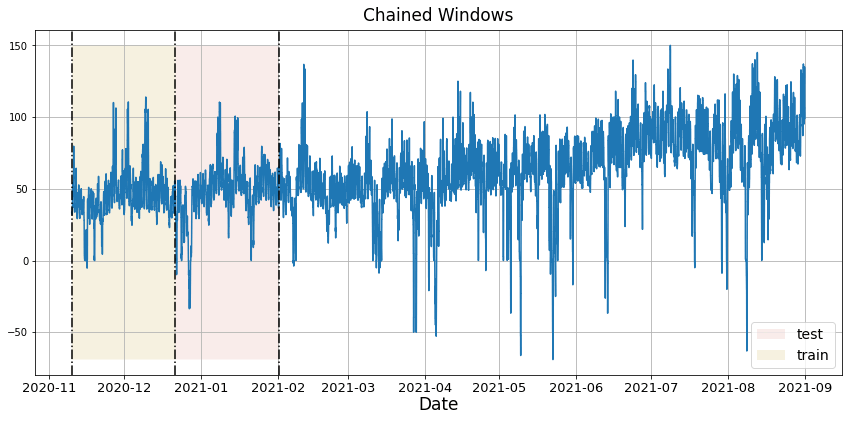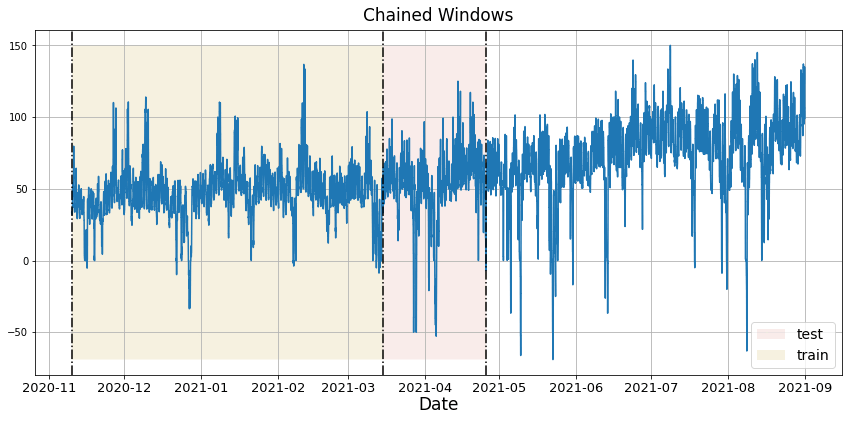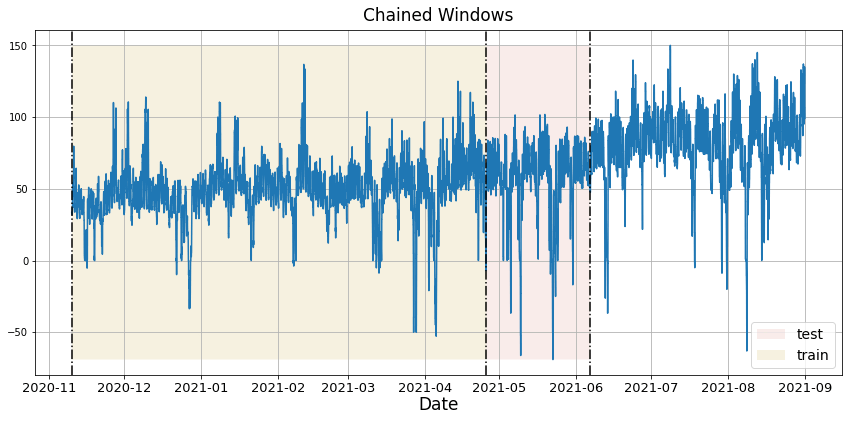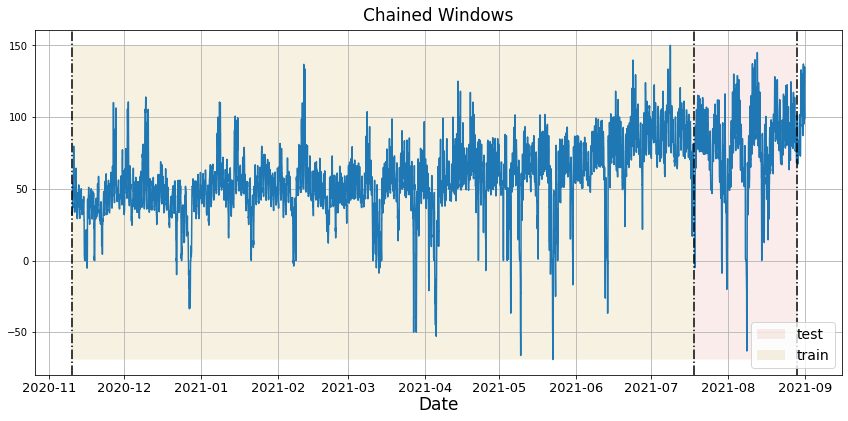
执行时间序列交叉验证

时间序列模型的交叉验证被认为是最佳实践，但大多数实现非常慢。statsforecast库将交叉验证实现为分布式操作，使过程变得不那么耗时。如果您有大型数据集，还可以使用Ray、Dask或Spark在分布式集群中执行交叉验证。

在这种情况下，我们希望评估每个模型在最后5个月的表现 (n_windows=)，每两个月进行一次预测 (step_size=50)。根据您的电脑，此步骤大约需要1分钟。

StatsForecast类的cross_validation方法接受以下参数。

df: 训练数据框
h (int): 表示未来h步的预测。在这种情况下，预测500小时之后的值。
step_size (int): 每个窗口之间的步长。换句话说：您希望多长时间运行一次预测过程。
n_windows(int): 用于交叉验证的窗口数量。换句话说：您希望评估过去多少次预测过程。

crossvalidation_df = sf.cross_validation(df=df,
                                         h=horizon,
                                         step_size=50,
                                         n_windows=5)

crossvaldation_df对象是一个新的数据框，其中包括以下列：

unique_id: 索引。如果您不喜欢使用索引，可以运行crossvalidation_df.resetindex()。
ds: 日期戳或时间索引
cutoff: n_windows的最后一个日期戳或时间索引。
y: 真实值
model: 模型名称和拟合值的列。

crossvalidation_df

	ds	cutoff	y	TSB
unique_id
1	2023-01-23 12:00:00	2023-01-23 11:00:00	0.0	0.000005
1	2023-01-23 13:00:00	2023-01-23 11:00:00	0.0	0.000005
1	2023-01-23 14:00:00	2023-01-23 11:00:00	0.0	0.000005
...	...	...	...	...
1	2023-02-21 13:00:00	2023-01-31 19:00:00	60.0	65.586456
1	2023-02-21 14:00:00	2023-01-31 19:00:00	20.0	65.586456
1	2023-02-21 15:00:00	2023-01-31 19:00:00	20.0	65.586456

2500 rows × 4 columns

评估模型

现在我们可以使用合适的准确度指标来计算预测的准确性。这里我们将使用均方根误差（RMSE）。为此，我们首先需要安装datasetsforecast，这是一个由Nixtla开发的Python库，其中包含计算RMSE的函数。

%%capture
!pip install datasetsforecast

from datasetsforecast.losses import rmse

计算RMSE的函数接受两个参数：

实际值。
预测值，在本例中为TSB模型。

rmse = rmse(crossvalidation_df['y'], crossvalidation_df["TSB"])
print("RMSE using cross-validation: ", rmse)

RMSE using cross-validation:  91.88035

鸣谢

我们要感谢Naren Castellon撰写本教程。

参考文献

Changquan Huang • Alla Petukhina. 施普林格系列（2022）。使用Python的应用时间序列分析与预测。
Ivan Svetunkov. 增强动态自适应模型（ADAM）的预测与分析
James D. Hamilton. 时间序列分析普林斯顿大学出版社, 新泽西州普林斯顿, 第1版, 1994年。
Nixtla参数。
Pandas可用频率。
Rob J. Hyndman和George Athanasopoulos（2018）。 “预测原则与实践，时间序列交叉验证”。。
季节性周期- Rob J Hyndman。

Give us a ⭐ on Github

目录

介绍

TSB 模型

TSB一般属性

加载库和数据

使用 plot 方法探索数据

自相关图

时间序列的分解

加性时间序列

乘性时间序列

将数据分为训练集和测试集

TSB模型的实现与StatsForecast

加载库

建立模型

拟合模型

预测方法

使用置信区间的预测方法

交叉验证

执行时间序列交叉验证

评估模型

鸣谢

参考文献

`TSB模型`的实现与StatsForecast