 摘要:
摘要:
- 我们介绍了MathChat,这是一个利用大型语言模型(LLMs),特别是GPT-4,来解决高级数学问题的对话框架。
- MathChat 提高了 LLM 在解决复杂数学问题上的表现,比基本提示和其他策略高出约 6%。这一改进在代数类别中尤为显著,准确率提高了 15%。
- 尽管取得了进展,GPT-4在使用有效的提示策略后,仍然难以解决非常具有挑战性的数学问题。需要进一步的改进,例如开发更具体的辅助模型或集成新工具和提示。
最近的大型语言模型(LLMs)如GTP-3.5和GPT-4在各种任务上展示了超越以往模型的惊人能力,例如文本生成、问答和代码生成。此外,这些模型可以通过对话与人类交流,并记住之前的上下文,使人类与它们互动变得更加容易。这些模型在我们的日常生活中扮演着越来越重要的角色,帮助人们完成不同的任务,如写电子邮件、总结文档和编写代码。
在这篇博客文章中,我们探讨了LLMs的解决问题的能力。具体来说,我们对它们解决高级数学问题的能力感兴趣,这可能代表了一类更广泛的问题,这些问题需要精确的推理,并且有确定的解决方案。
我们介绍MathChat,一个专为使用LLMs解决复杂数学问题而设计的对话框架。该框架利用了最先进LLMs的聊天优化功能,其中一个用户代理和一个LLM助手共同解决数学问题。我们还测试了之前的提示技术以进行比较。
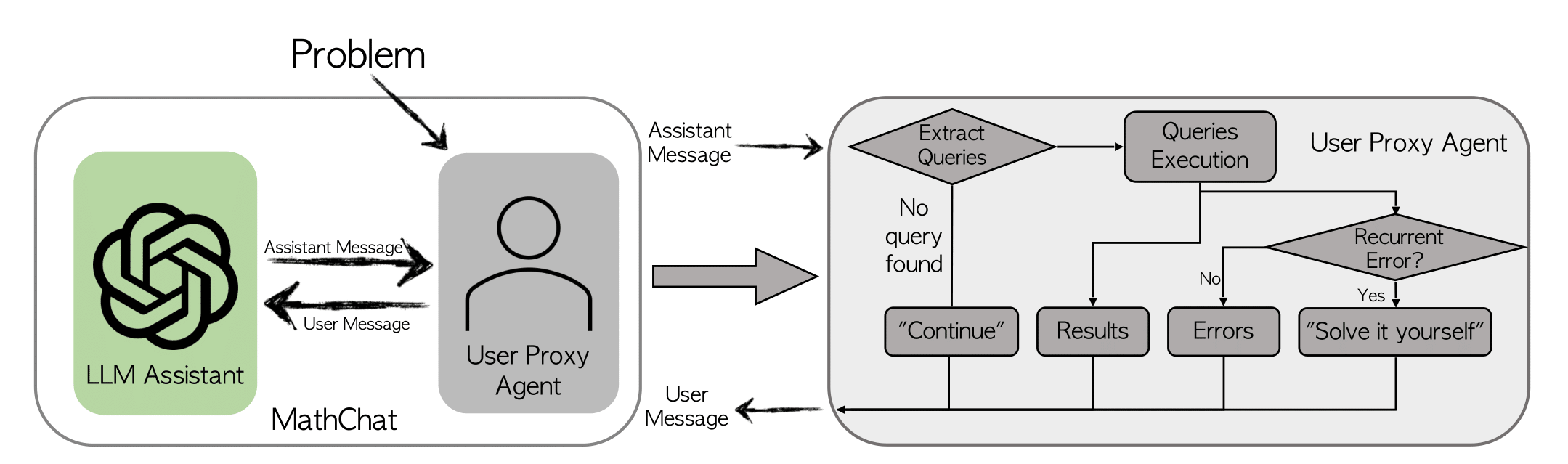
MathChat框架
MathChat模拟了LLM助手和用户代理之间的对话。正如其名称所示,用户代理充当用户的代理,负责与LLM助手进行沟通,并以期望的方式继续对话。
代理代理首先向LLM助手展示一个数学问题,并通过一个初始提示来引导助手如何协同工作以解决问题。我们在初始提示中融入了现有的提示方法,如CoT(思维链)和工具使用。提示的关键组成部分包括:
-
工具使用提示: 这部分指导LLM助理以正确的格式使用Python代码来解决问题,允许用户代理解析代码并提供适当的结果。
-
问题解决策略选择提示:助手被指示从三种潜在的问题解决策略中选择一种,包括:
- 编写一个Python程序直接解决问题。
- 直接解决问题而不使用Python,这可以锻炼LLMs的固有推理能力。
- 使用Python逐步解决问题。当前两种策略不适用时应使用此方法。
-
最终答案封装提示: 这部分指示助手将最终答案放在\boxed中。
MathChat中的提示设计非常灵活,可以轻松地改进以包含其他工具,比如Wolfram Alpha。
让我们来看一个用户代理和LLM助手(GPT-4)之间的示例。对话重点是如何使用Python解决不等式问题。(对话已修改以提高可读性。)
| 参与者 | 对话 |
|---|---|
| 用户代理 | (初始提示:让我们用Python解决一个数学问题...) 问题:找到所有满足不等式 (2x+10)(x+3) < (3x+9)(x+8) 的x。用区间表示法表达你的答案。 |
| LLM assistant | 解决这个问题的关键思想是找到临界点,即不等式相等的点。然后,测试这些临界点之间的区间,以找到不等式成立的区间。 |
| LLM assistant (continued) | Here's Python code to find the critical points: from sympy import symbols, Eq, solve; x = symbols("x"); lhs = (2*x + 10)*(x + 3); rhs = (3*x + 9)*(x + 8); equation = Eq(lhs, rhs); critical_points = solve(equation, x); critical_points |
| 用户代理 | 关键点是:[-14, -3] |
| LLM助手 | 我们发现临界点是 x = -14 和 x = -3。现在我们将测试这些临界点之间的区间以及临界点前后的点。区间为:x < -14,-14 < x < -3,x > -3。 |
| LLM assistant (continued) | Here's Python code to test the inequality for each interval: from sympy import symbols; x = symbols("x"); inequality = (2*x + 10)*(x + 3) < (3*x + 9)*(x + 8); test_points = [-15, -5, 0]; intervals = []; for point in test_points: if inequality.subs(x, point): intervals.append(point); intervals |
| 用户代理 | 不等式成立的时间间隔为测试点:[-15, 0] |
| LLM助手 | 我们已经测试了区间,发现不等式在以下情况成立:1. x < -14(测试点:-15)2. x > -3(测试点:0)。因此,不等式 (2x+10)(x+3) < (3x+9)(x+8) 的解是 x ∈ (-∞, -14) ∪ (-3, ∞) |
实验设置
我们评估了MathChat带来的改进。
在实验中,我们专注于MATH数据集中的第5级问题,这些问题由高中竞赛题目组成。这些问题包括定理的应用和复杂方程的推导,即使对本科生来说也具有挑战性。我们评估了数据集中的7个类别中的6个(不包括几何):初级代数、代数、数论、计数与概率、中级代数和微积分预备课程。
我们评估GPT-4并使用OpenAI API的默认配置。为了获取最终性能,我们手动将最终答案与正确答案进行比较。对于普通提示、程序合成和MathChat,我们让GPT-4将最终答案放在\boxed中,并将PoT中的函数返回值作为最终答案。
为了进行比较,我们还评估了以下方法:
-
基本提示: 评估GPT-4的直接问题解决能力。使用的提示词是:"仔细解决问题。将最终答案放在\boxed"。
-
思维程序 (PoT): 使用零样本PoT提示,要求模型创建一个求解器函数来解决问题并返回最终答案。
-
程序合成(PS)提示: 类似于PoT,它提示模型编写一个程序来解决问题。使用的提示是:"编写一个程序来回答以下问题:{Problem}"。
实验结果
使用不同方法解决MATH数据集中不同类别难度等级为5的所有问题的准确性如下所示:
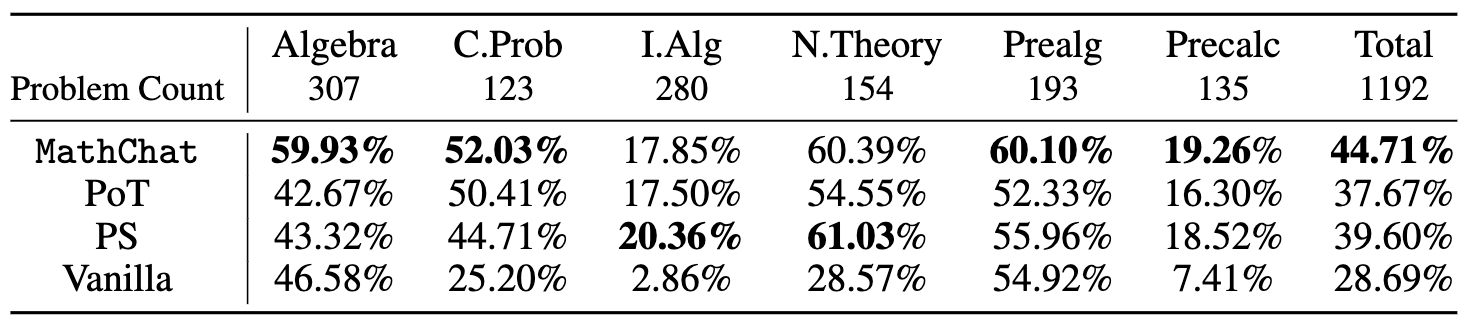
我们发现,与展示了GPT-4内在能力的基本提示相比,在PoT或PS策略的背景下使用Python,整体准确性提高了约10%。这一增长主要出现在涉及更多数值操作的类别中,如计数与概率和数论,以及在更复杂的类别中,如中级代数和预微积分。
对于代数和预代数等类别,PoT和PS几乎没有改进,某些情况下甚至导致准确性下降。然而,与PoT和PS相比,MathChat能够将总准确性提高约6%,在所有类别中表现出竞争性能。值得注意的是,MathChat在代数类别中的准确性比其他方法提高了约15%。需要注意的是,中等代数和预微积分等类别对所有方法仍然具有挑战性,只有约20%的问题被准确解决。
实验代码可以在repository找到。 我们现在使用AutoGen中的交互式代理提供MathChat的实现。有关示例用法,请参见notebook。
未来方向
尽管MathChat相比以前的方法有所改进,但结果表明,对于最近强大的LLMs(如GPT-4)来说,即使是借助外部工具,解决复杂的数学问题仍然具有挑战性。
可以进一步努力增强这个框架或一般数学问题解决能力:
- 尽管让模型使用像Python这样的工具可以减少计算错误,但LLMs仍然容易出现逻辑错误。像自一致性(采样多个解决方案并对最终答案进行多数表决)或自验证(使用另一个LLM实例检查答案是否正确)这样的方法可能会提高性能。
- 有时候,LLM能否解决问题取决于它使用的计划。有些计划需要的计算和逻辑推理较少,因此出错的余地也较小。
- MathChat 有潜力被改编为一个 copilot 系统,该系统可以帮助用户解决数学问题。这个系统可以让用户更多地参与到问题解决过程中,可能增强学习效果。
进一步阅读
您是否正在开发涉及数学问题解决的应用?您是否希望对基于LLM的代理在数学问题解决中的应用进行更多研究或支持?请加入我们的Discord服务器进行讨论。
