AdaSum with Horovod¶
自适应求和(AdaSum)是一种新颖的算法,用于改进深度学习模型的分布式数据并行训练。这种改进体现在多个方面:在某些情况下减少达到相同精度所需的步骤数,并允许扩展到更多训练工作节点,而不会影响学习率和收敛稳定性。 AdaSum可与Horovod和PyTorch/TensorFlow配合使用。
目录
AdaSum算法介绍¶
将深度神经网络训练扩展到多个GPU总会带来收敛性能下降的问题。这是因为随着批量大小的增加,梯度被平均化,每个样本的学习率变得更小。为解决这一问题,通常会按比例增加学习率,但这可能导致模型参数发散。AdaSum在不引入任何超参数的情况下解决了这两个问题。
假设有两个来自不同GPU(g1和g2)的几乎平行的梯度,它们需要按照下图所示进行归约。归约的两种常见做法是g1+g2(灰色向量)或(g1+g2)/2(绿色向量)。g1+g2可能导致模型发散,因为它实际上是以g1或g2的两倍幅度在g1或g2的方向上移动。因此,通常(g1+g2)/2更安全且更可取。注意,(g1+g2)/2对分量g1和g2的惩罚是相等的。
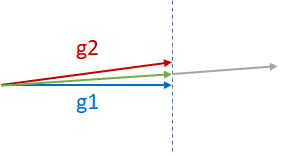
现在考虑下图中的两个正交梯度 g1 和 g2。由于 g1 和 g2 处于两个不同的维度且彼此独立,g1+g2 可能不会导致发散。
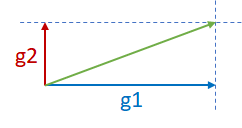
最后,考虑第三种场景,其中g1和g2既不平行也不正交,如下图所示。在这种情况下,直接求和可能导致发散,AdaSum通过从g2中减去g1在g2上的投影的一半(粉色向量),从g1中减去g2在g1上的投影的一半(橙色向量),并将两个分量相加,来控制整体梯度更新的效果。
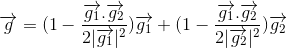
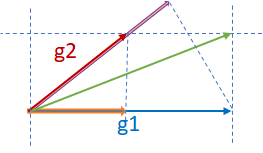
当 g1 和 g2 正交时,该公式简化为求和;当 g1 和 g2 平行时,则简化为平均值。
这一理念同样适用于多个梯度。假设有来自2^n个不同GPU的2^n个梯度。AdaSum通过归纳方式将梯度两两配对,并使用上述方法进行归约,直到所有梯度被归约为一个梯度。因此,在当前实现中,AdaSum要求节点数量必须是2的幂次方。
AdaSum的分布式优化器¶
AdaSum使用分布式AdaSum优化器在每一步后更新模型的权重。在通常的数据并行训练场景中,通过在所有节点上进行反向传播独立计算梯度,执行归约(平均梯度)以使所有节点现在拥有相同的梯度,然后更新模型的权重。
AdaSum的分布式优化器首先从当前本地小批量的反向传播步骤中获取本地梯度。此时不执行归约操作,而是对本地梯度应用优化函数以执行权重更新。然后,获取更新前后权重之间的差异(即delta),随后对这个delta而非梯度进行归约。一旦所有工作节点都拥有相同的delta,权重更新步骤便通过初始权重与delta之和来执行。
由于AdaSum的性质要求它在梯度的完整幅度上操作,新添加的分布式优化器利用优化器执行步骤前后权重幅度的差异来提供更准确的估计。
Installation and Usage Instructions¶
AdaSum 可以与 Horovod 和 Pytorch/TensorFlow 一起使用和实验。
此外,使用 AdaSum 与 Horovod 有两种选择:使用消息传递接口(MPI)和使用 NCCL。 任何有效的 MPI 实现都可以使用,但 AdaSum 已经通过 OpenMPI 和 IntelMPI 进行了测试。
操作模式¶
Adasum 可根据可用硬件设置以以下方式使用。
纯CPU¶
当处理多节点的硬件设置时,每个节点都有工作GPU,这些GPU没有通过像NVLink这样的高速互连连接,通信通过CPU进行,通过MPI的AdaSum可以用于节点内和节点间的通信。在这种情况下,所有的AdaSum操作都在CPU上执行。
如果硬件设置允许使用不同的模式,如环形或分层模式,则必须使用这些模式以获得最高的性能优势。
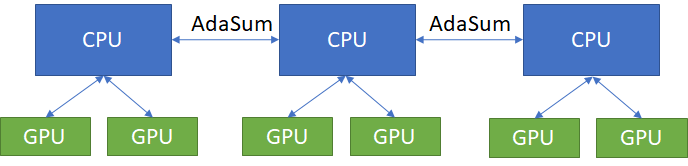
环形¶
在特定配置的机器上(每个带有8个GPU的DGX1节点),可以使用环形模式替代纯CPU模式。该模式在节点间通信方面与纯CPU模式相同,但能够在节点内进行通信而无需经过CPU。这是通过利用CUDA感知的MPI(使用UCX支持构建的OpenMPI)来实现的,以便允许节点内GPU到GPU的直接通信。这带来了与纯CPU模式相同的收敛优势,但在支持该模式的节点上具有更好的吞吐量。
环形模式目前仅在DGX1节点上受支持,每个节点拥有8个GPU。

分层¶
在硬件不支持环形模式,但需要比纯CPU模式更高吞吐量的情况下,可以使用分层模式替代。
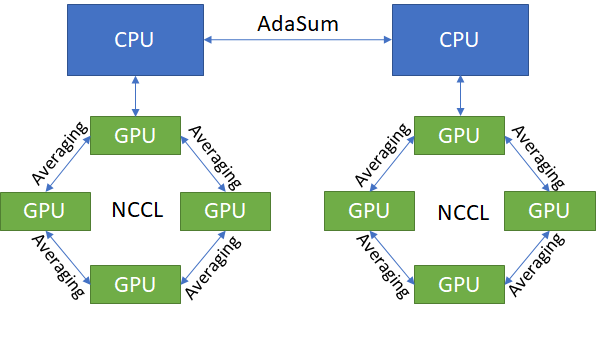
分层模式的功能类似于环形模式,不同之处在于使用NCCL在节点内进行常规平均,而不是使用CUDA-aware MPI执行类似AdaSum的环形操作。请注意,分层模式也适用于任何硬件配置,并不局限于DGX1服务器。
在实践中,分层结构能提供最佳吞吐量,但由于部分操作采用常规平均方式,会降低AdaSum的收敛优势。根据经验法则,在大型节点集群(≥8个节点)中,收敛效益的下降通常微不足道,因为这种情况下会执行足够的节点间AdaSum操作。这是理想的分层场景。
在较小集群上使用分层模式的另一个原因是当不支持环形模式时,CPU模式的吞吐量实在太低而无法使用。请注意,在这些情况下,与完全不使用AdaSum相比,收敛性的提升可能微乎其微。
应使用的学习率等于单个工作器(GPU)的最佳学习率乘以节点上本地GPU的数量。在非常大的集群上,再乘以1.5-2.0倍的额外因子可能会得到更好的结果,但这并不保证,只有在仅按本地大小缩放不足以实现良好收敛时才应尝试。
代码修改¶
TensorFlow和Pytorch都新增了一个分布式优化器,以支持AdaSum算法。
已向 DistributedOptimizer 和 allreduce API 添加了一个可选参数 op,供用户指定要执行的操作。 当指定 op=hvd.AdaSum 时,将使用新的优化器。
AdaSum在扩展到大批次大小时非常高效。DistributedOptimizer的backward_passes_per_step参数可用于梯度累积,从而扩展到更大的有效批次大小,而不会受到GPU内存的限制。
TensorFlow¶
分布式优化器
opt = tf.train.AdamOptimizer(0.001)
opt = hvd.DistributedOptimizer(opt, backward_passes_per_step=5, op=hvd.AdaSum)
Allreduce
hvd.allreduce(tensor, op=hvd.AdaSum)
PyTorch¶
分布式优化器
optimizer = optim.SGD(model.parameters(), lr=args.lr, momentum=args.momentum)
optimizer = hvd.DistributedOptimizer(optimizer, named_parameters=model.named_parameters(), compression=compression, backward_passes_per_step = 5, op=hvd.AdaSum)
Allreduce
hvd.allreduce(tensor, op=hvd.AdaSum)
案例研究¶
平方与立方优化¶
一个简单的案例研究以理解AdaSum的行为
为了理解AdaSum与平均相比的行为和潜在优势,考虑一个使用AdaSum的平方优化简单实验。这里的目标是估计一个二次多项式的系数。特征通过随机采样均匀分布生成,并通过可指定的x_max因子进行缩放。这设置了用于估计系数的数据复杂度。此外,学习率和用于Allreduce的操作也可以指定。真实标签使用原始真实系数计算,不添加任何噪声。
为了估计系数,使用了随机梯度下降法。一旦梯度连续两次运行结果为零,训练就会停止。这种优化可以在不同的学习率、工作器数量和数据范围(由x_max设定)下进行。这也可以修改为一个三次优化问题。
本实验可以通过jupyter笔记本adasum_bench.ipynb运行,模型定义在adasum_small_model.py中。
在使用不同数量的工作节点进行实验时,我们可以针对使用普通SGD作为优化器的简单场景得出以下结论:
关于收敛所需的步数:对于相同的问题,AdaSum 在更少的步数内达到相同的精度(在此情况下为100%),相比之下求平均方法需要更多步数。根据问题的复杂度,对于较简单的平方参数优化,这种减少幅度可达50%。
关于针对更多工作节点调整学习率: 对于传统的平均方法,当工作节点数量增加而本地批次大小保持不变时,这会增大全局批次规模,从而对梯度产生更强的平滑效应。为了加快收敛速度,建议按照论文Accurate, Large Minibatch SGD: Training ImageNet in 1 Hour中的推荐,将学习率按工作节点数量进行相应放大。
从这个例子中,我们看到使用AdaSum时,学习率(LR)不需要与工作节点数量线性缩放,而更好的缩放因子应为2-2.5。
关于使用学习率衰减: 使用AdaSum时,我们发现一种正则化效果已经在梯度上发生。随着训练的进行,梯度幅度减小,模拟了与学习率衰减相同的效果。尽管训练更复杂的模型可能需要一些衰减,但必须记住这个结果,因为可能不需要相同程度的衰减。
关键要点¶
AdaSum 确保即使在大有效批次大小下也能实现正确的收敛行为。
随着秩的数量增加,如果使用CPU进行AdaSum归约,学习率不需要线性缩放。相比于单工作器的最佳学习率,较好的缩放因子应在2-2.5之间。
如果使用 HOROVOD_GPU_OPERATIONS=NCCL 标志编译 Horovod,应使用的学习率等于单个工作器(GPU)的最佳学习率乘以节点本地 GPU 数量。在非常大的集群上,再额外乘以 1.5-2.0 倍可能会带来更好的结果,但这并不保证,只有在仅按本地大小缩放无法实现良好收敛时才应尝试。
Pytorch 的 fp16 格式训练目前尚不支持。将 Apex 集成到新优化器中,以在 Pytorch 中实现带有 AdaSum 的完整混合精度训练正在进行中。
当使用HOROVOD_GPU_OPERATIONS=NCCL标志编译Horovod并在单节点上运行训练时,仅通过NCCL库进行平均化来执行归约操作,在此配置中不会使用AdaSum算法。
