3. 欠采样#

处理不平衡数据集的一种方法是减少除少数类之外的所有类别的观测数量。少数类是指观测数量最少的类别。这一组中最著名的算法是随机欠采样，即从目标类别中随机移除样本。

但是还有许多其他算法可以帮助我们减少数据集中的观测数量。这些算法可以根据它们的欠采样策略分为以下几类：

原型生成方法。
原型选择方法。

在后者中，我们发现：

受控欠采样
清洁方法

我们将在本文档中讨论不同的算法。

3.1. 原型生成#

给定一个原始数据集 \(S\)，原型生成算法将生成一个新的集合 \(S'\)，其中 \(|S'| < |S|\) 且 \(S' \not\subset S\)。换句话说，原型生成技术将减少目标类别中的样本数量，但剩余的样本是从原始集合中生成而不是选择的。

ClusterCentroids 使用K-means来减少样本数量。因此，每个类将通过K-means方法的质心而不是原始样本来合成：

>>> from collections import Counter
>>> from sklearn.datasets import make_classification
>>> X, y = make_classification(n_samples=5000, n_features=2, n_informative=2,
...                            n_redundant=0, n_repeated=0, n_classes=3,
...                            n_clusters_per_class=1,
...                            weights=[0.01, 0.05, 0.94],
...                            class_sep=0.8, random_state=0)
>>> print(sorted(Counter(y).items()))
[(0, 64), (1, 262), (2, 4674)]
>>> from imblearn.under_sampling import ClusterCentroids
>>> cc = ClusterCentroids(random_state=0)
>>> X_resampled, y_resampled = cc.fit_resample(X, y)
>>> print(sorted(Counter(y_resampled).items()))
[(0, 64), (1, 64), (2, 64)]

下图展示了这种欠采样。

_images/sphx_glr_plot_comparison_under_sampling_001.png

ClusterCentroids 提供了一种有效的方式，通过减少样本数量来表示数据集群。请记住，这种方法要求您的数据被分组到集群中。此外，应设置质心的数量，使得欠采样的集群能够代表原始集群。

警告

ClusterCentroids 支持稀疏矩阵。然而，生成的新样本并不是特别稀疏。因此，即使结果矩阵是稀疏的，算法在这方面也会效率低下。

3.2. 原型选择#

原型选择算法将从原始集合\(S\)中选择样本，生成一个数据集\(S'\)，其中\(|S'| < |S|\)且\(S' \subset S\)。换句话说，\(S'\)是\(S\)的一个子集。

原型选择算法可以分为两组：(i) 受控欠采样技术和(ii) 清理欠采样技术。

受控欠采样方法将多数类中的观察数量减少到用户指定的任意样本数量。通常，它们将观察数量减少到少数类中观察到的样本数量。

相比之下，清理欠采样技术通过移除“噪声”或“太容易分类”的观察结果来“清理”特征空间，具体取决于所使用的方法。每个类别中的最终观察数量因清理方法而异，用户无法指定。

3.2.1. 受控欠采样技术#

受控欠采样技术将目标类别的观测数量减少到用户指定的数量。

3.2.1.1. 随机欠采样#

RandomUnderSampler 是一种快速且简单的方法，通过随机选择目标类别的数据子集来平衡数据：

>>> from imblearn.under_sampling import RandomUnderSampler
>>> rus = RandomUnderSampler(random_state=0)
>>> X_resampled, y_resampled = rus.fit_resample(X, y)
>>> print(sorted(Counter(y_resampled).items()))
[(0, 64), (1, 64), (2, 64)]

_images/sphx_glr_plot_comparison_under_sampling_002.png

RandomUnderSampler 允许通过将 replacement 设置为 True 来对数据进行自举。当存在多个类别时，每个目标类别都会被独立地进行欠采样：

>>> import numpy as np
>>> print(np.vstack([tuple(row) for row in X_resampled]).shape)
(192, 2)
>>> rus = RandomUnderSampler(random_state=0, replacement=True)
>>> X_resampled, y_resampled = rus.fit_resample(X, y)
>>> print(np.vstack(np.unique([tuple(row) for row in X_resampled], axis=0)).shape)
(181, 2)

RandomUnderSampler 处理异构数据类型，即数值型、类别型、日期型等：

>>> X_hetero = np.array([['xxx', 1, 1.0], ['yyy', 2, 2.0], ['zzz', 3, 3.0]],
...                     dtype=object)
>>> y_hetero = np.array([0, 0, 1])
>>> X_resampled, y_resampled = rus.fit_resample(X_hetero, y_hetero)
>>> print(X_resampled)
[['xxx' 1 1.0]
 ['zzz' 3 3.0]]
>>> print(y_resampled)
[0 1]

RandomUnderSampler 也支持将 pandas 数据框作为下采样的输入：

>>> from sklearn.datasets import fetch_openml
>>> df_adult, y_adult = fetch_openml(
...     'adult', version=2, as_frame=True, return_X_y=True)
>>> df_adult.head()  
>>> df_resampled, y_resampled = rus.fit_resample(df_adult, y_adult)
>>> df_resampled.head()  

NearMiss 添加了一些启发式规则来选择样本 [MZ03]。 NearMiss 实现了3种不同的启发式方法，可以通过参数 version 进行选择：

>>> from imblearn.under_sampling import NearMiss
>>> nm1 = NearMiss(version=1)
>>> X_resampled_nm1, y_resampled = nm1.fit_resample(X, y)
>>> print(sorted(Counter(y_resampled).items()))
[(0, 64), (1, 64), (2, 64)]

正如下一节所述，NearMiss 启发式规则基于最近邻算法。因此，参数 n_neighbors 和 n_neighbors_ver3 接受从 scikit-learn 的 KNeighborsMixin 派生的分类器。前者用于计算到邻居的平均距离，而后者用于预选感兴趣的样本。

3.2.1.2. 数学公式#

让正样本成为属于目标类别的样本，这些样本将被欠采样。负样本指的是来自少数类别的样本（即最不具代表性的类别）。

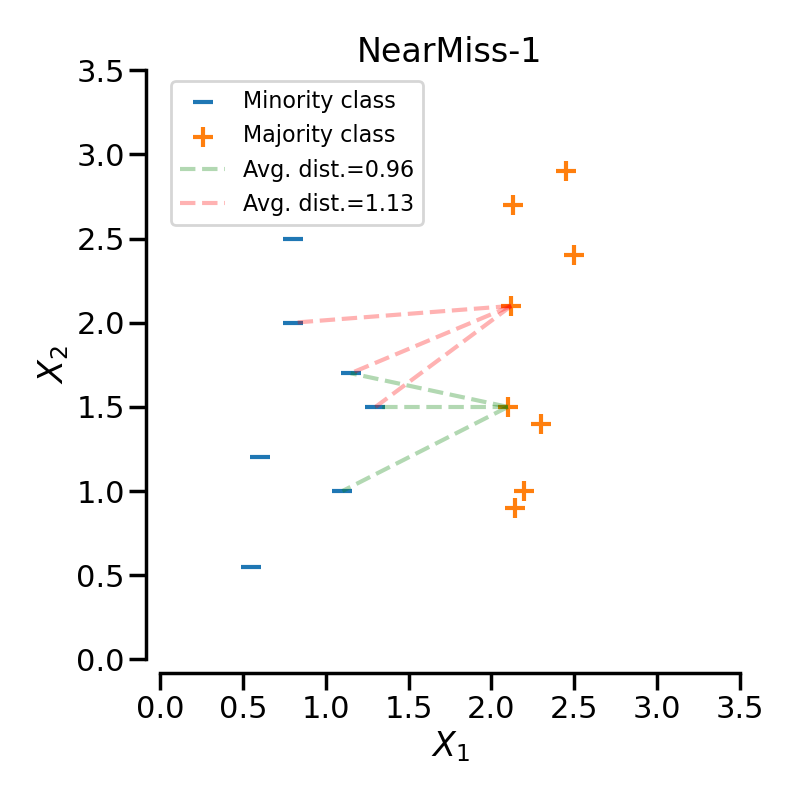
NearMiss-1 选择那些到负类中 \(N\) 个最近样本的平均距离最小的正样本。

_images/sphx_glr_plot_illustration_nearmiss_001.png

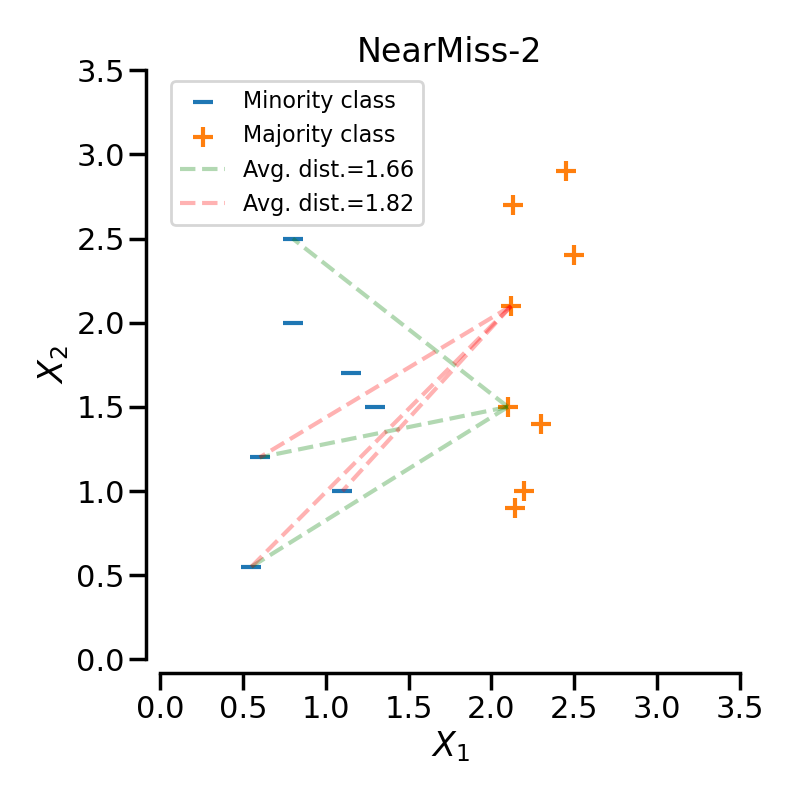
NearMiss-2 选择那些与负类中最远的 \(N\) 个样本的平均距离最小的正样本。

_images/sphx_glr_plot_illustration_nearmiss_002.png

NearMiss-3 是一个两步算法。首先，对于每个负样本，将保留它们的 \(M\) 个最近邻居。然后，选择的阳性样本是那些到 \(N\) 个最近邻居的平均距离最大的样本。

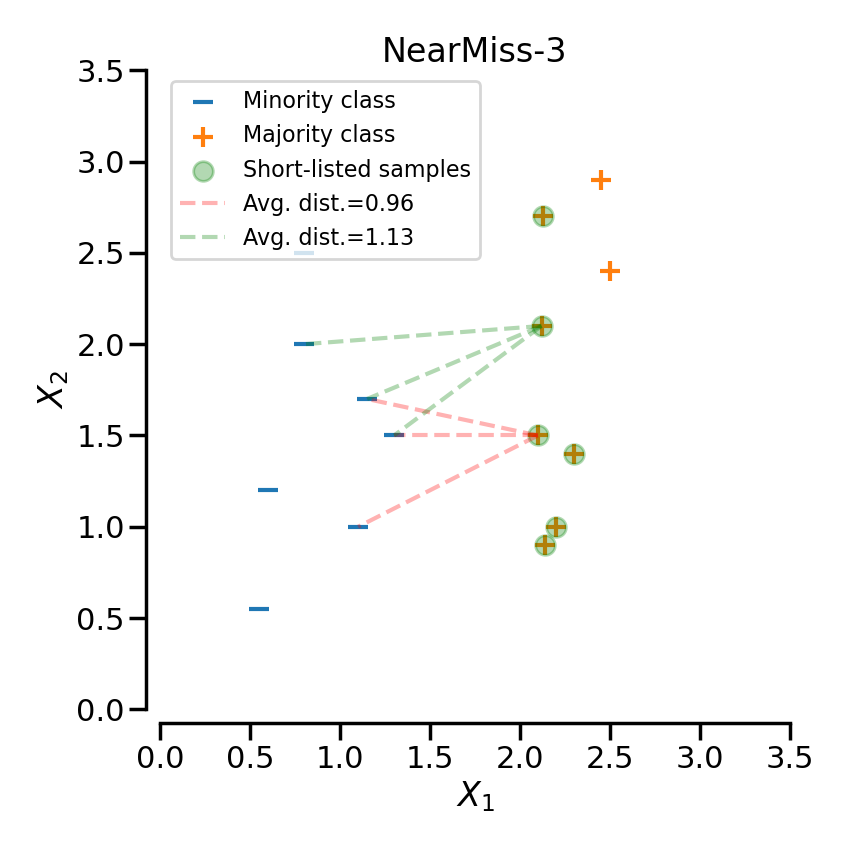
_images/sphx_glr_plot_illustration_nearmiss_003.png

在下一个示例中，不同的NearMiss变体被应用于之前的玩具示例。可以看出，每种情况下获得的决策函数是不同的。

在对特定类别进行欠采样时，NearMiss-1可能会受到噪声的影响而改变。实际上，这意味着目标类别的样本将在这些样本周围被选择，如下图所示中的黄色类别所示。然而，在正常情况下，边界附近的样本将被选择。NearMiss-2不会有这种效果，因为它不关注最近的样本，而是关注最远的样本。我们可以想象，噪声的存在也可能主要在有边缘异常值的情况下改变采样。NearMiss-3可能是由于第一步样本选择而受噪声影响最小的版本。

_images/sphx_glr_plot_comparison_under_sampling_003.png

3.2.2. 清理欠采样技术#

清理欠采样方法通过移除“噪声”观察或“太容易分类”的观察来“清理”特征空间，具体取决于方法。每个目标类别中的最终观察数量因清理方法而异，用户无法指定。

3.2.2.1. Tomek的链接#

当来自不同类别的两个样本互为最近邻时，存在Tomek链接。

在数学上，来自不同类别的两个样本 \(x\) 和 \(y\) 之间的 Tomek 链接被定义为对于任何样本 \(z\)：

\[d(x, y) < d(x, z) \text{ and } d(x, y) < d(y, z)\]

其中 \(d(.)\) 是两个样本之间的距离。

TomekLinks 检测并移除Tomek的链接 [Tom76b]。其基本思想是，Tomek的链接是噪声或难以分类的观察结果，不会帮助算法找到合适的分界边界。

在下图中，类别\(+\)和类别\(-\)之间的Tomek链接以绿色高亮显示：

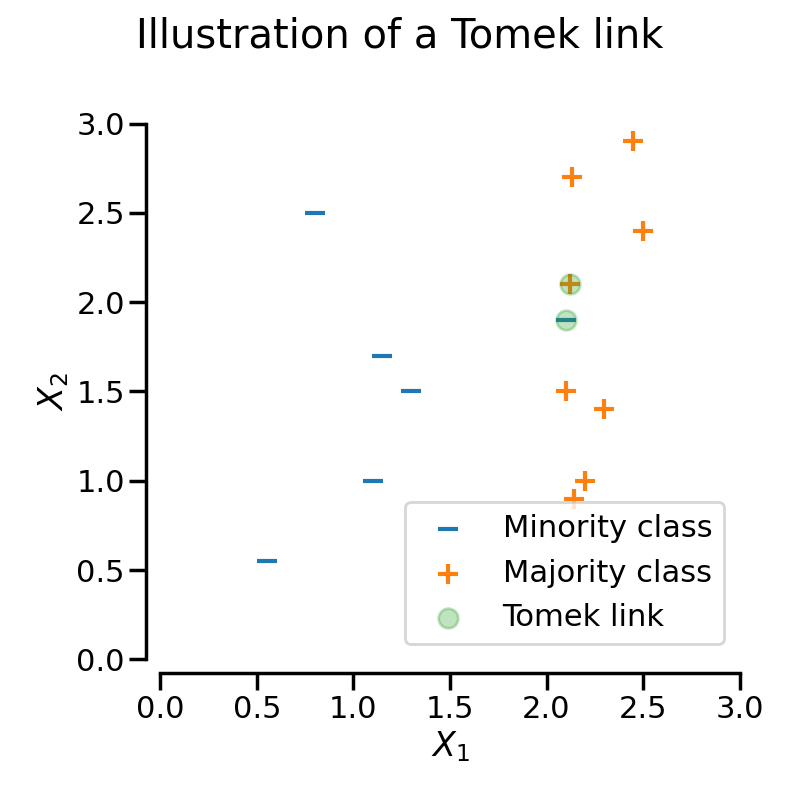
_images/sphx_glr_plot_illustration_tomek_links_001.png

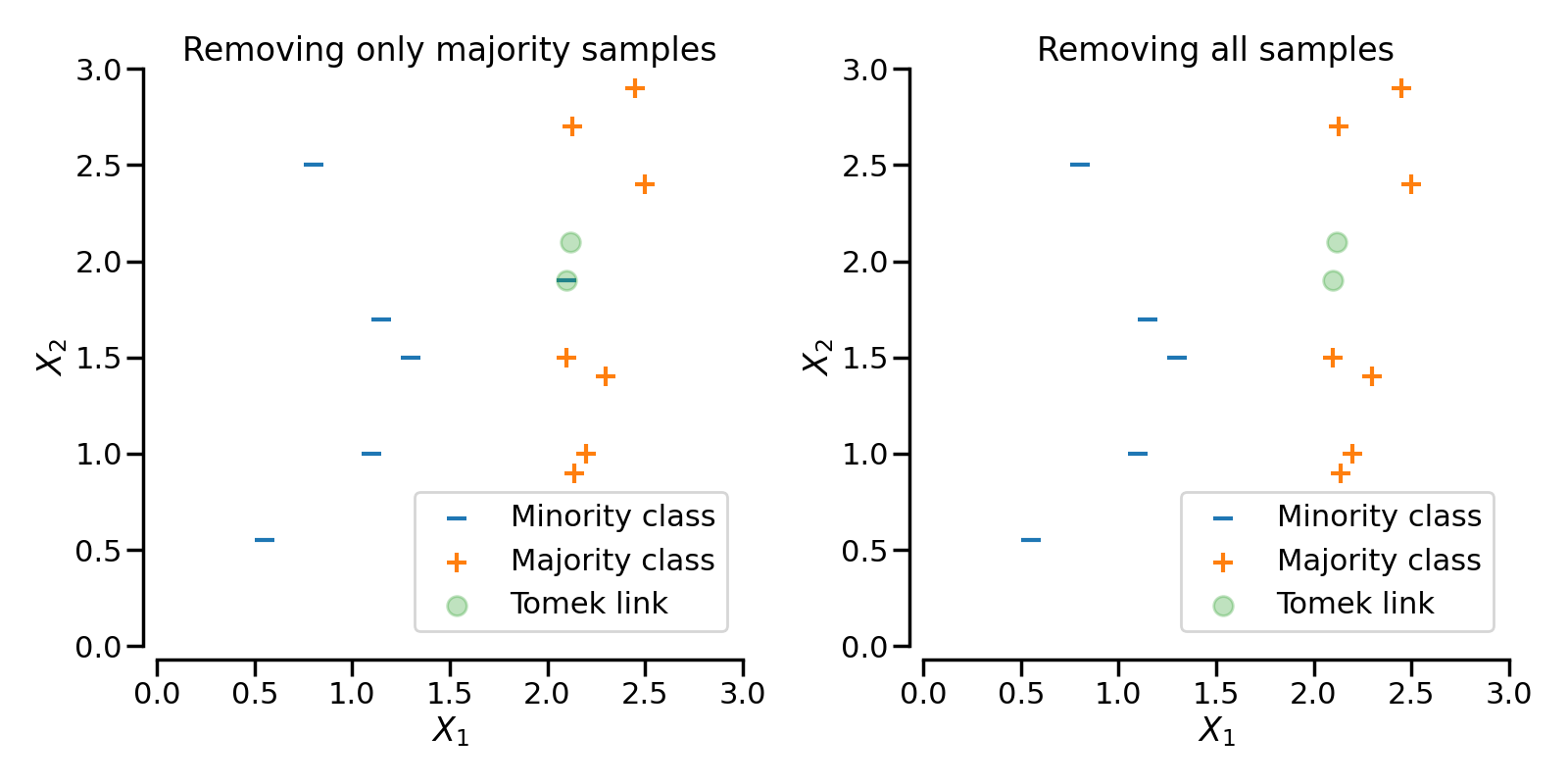
当TomekLinks找到一个Tomek的链接时，它可以移除多数类的样本，或者两者都移除。参数sampling_strategy控制将移除链接中的哪些样本。默认情况下（即sampling_strategy='auto'），它将移除多数类的样本。通过将sampling_strategy设置为'all'，可以移除多数类和少数类的样本。

下图展示了这种行为：在左侧，仅移除了多数类的样本，而在右侧，移除了整个Tomek的链接。

_images/sphx_glr_plot_illustration_tomek_links_002.png

3.2.2.2. 使用最近邻编辑数据#

3.2.2.2.1. 编辑最近邻#

编辑最近邻方法使用K-最近邻来识别目标类样本的邻居，然后如果任何或大多数邻居来自不同类别，则移除观察结果 [Wil72]。

EditedNearestNeighbours 执行以下步骤：

使用整个数据集训练一个K-最近邻算法。
找到每个观测值的K个最近邻居（仅针对目标类别）。
如果任何或大多数邻居属于不同的类别，则移除观察结果。

以下是代码实现：

>>> sorted(Counter(y).items())
[(0, 64), (1, 262), (2, 4674)]
>>> from imblearn.under_sampling import EditedNearestNeighbours
>>> enn = EditedNearestNeighbours()
>>> X_resampled, y_resampled = enn.fit_resample(X, y)
>>> print(sorted(Counter(y_resampled).items()))
[(0, 64), (1, 213), (2, 4568)]

重新表述步骤3，EditedNearestNeighbours 将保留多数类中的观察值，当大多数或所有其邻居来自同一类时。为了控制这种行为，我们分别设置kind_sel='mode' 或 kind_sel='all'。因此，kind_sel='all' 比 kind_sel='mode' 更不保守，导致移除更多的样本：

>>> enn = EditedNearestNeighbours(kind_sel="all")
>>> X_resampled, y_resampled = enn.fit_resample(X, y)
>>> print(sorted(Counter(y_resampled).items()))
[(0, 64), (1, 213), (2, 4568)]
>>> enn = EditedNearestNeighbours(kind_sel="mode")
>>> X_resampled, y_resampled = enn.fit_resample(X, y)
>>> print(sorted(Counter(y_resampled).items()))
[(0, 64), (1, 234), (2, 4666)]

参数 n_neighbors 接受整数。该整数指的是每个样本要检查的邻居数量。它也可以接受从 scikit-learn 的 KNeighborsMixin 派生的分类器。当传递分类器时，请注意，如果你传递一个 3-最近邻分类器，清理时只会检查 2 个邻居，因为第三个样本是用于欠采样的样本，因为它是 fit 时提供的样本的一部分。

3.2.2.2.2. 重复编辑最近邻#

RepeatedEditedNearestNeighbours 扩展了 EditedNearestNeighbours，通过多次重复该算法 [Tom76a]。通常，重复该算法会删除更多的数据：

>>> from imblearn.under_sampling import RepeatedEditedNearestNeighbours
>>> renn = RepeatedEditedNearestNeighbours()
>>> X_resampled, y_resampled = renn.fit_resample(X, y)
>>> print(sorted(Counter(y_resampled).items()))
[(0, 64), (1, 208), (2, 4551)]

用户可以通过参数max_iter设置编辑最近邻方法的重复次数。

重复将在以下情况下停止：

达到最大迭代次数，或
不再移除更多的观察值，或者
其中一个多数类变成了少数类，或者
在欠采样过程中，多数类之一消失了。

3.2.2.2.3. 所有KNN#

AllKNN 是 RepeatedEditedNearestNeighbours 的一种变体，其中在每一轮 EditedNearestNeighbours 中评估的邻居数量会增加。它从基于1-最近邻的编辑开始，并在每次迭代中将邻域增加1 [Tom76a]:

>>> from imblearn.under_sampling import AllKNN
>>> allknn = AllKNN()
>>> X_resampled, y_resampled = allknn.fit_resample(X, y)
>>> print(sorted(Counter(y_resampled).items()))
[(0, 64), (1, 220), (2, 4601)]

AllKNN 当检查的最大邻居数达到用户通过参数 n_neighbors 确定的值时，或者当多数类变为少数类时，停止清理。

在下面的示例中，我们看到EditedNearestNeighbours、RepeatedEditedNearestNeighbours和AllKNN在清理类之间边界处的“噪声”样本时具有相似的影响。

_images/sphx_glr_plot_comparison_under_sampling_004.png

3.2.2.3. 浓缩最近邻#

CondensedNearestNeighbour 使用1最近邻规则来迭代决定是否应移除一个样本 [Har68]。算法运行如下：

获取集合 \(C\) 中的所有少数样本。
在目标类别（需要欠采样的类别）中添加一个样本，并将该类别中的所有其他样本放入集合 \(S\) 中。
在 \(C\) 上训练一个1-最近邻模型。
遍历集合 \(S\) 中的样本，逐个样本进行分类，使用1最近邻规则（在3中训练）。
如果样本被错误分类，将其添加到\(C\)，然后转到步骤6。
重复步骤3到5，直到\(S\)中的所有观测值都被检查完毕。

最终的数据集是\(S\)，包含来自少数类的所有观察值以及来自多数类的那些被连续的1-最近邻算法错误分类的观察值。

CondensedNearestNeighbour 可以按以下方式使用：

>>> from imblearn.under_sampling import CondensedNearestNeighbour
>>> cnn = CondensedNearestNeighbour(random_state=0)
>>> X_resampled, y_resampled = cnn.fit_resample(X, y)
>>> print(sorted(Counter(y_resampled).items()))
[(0, 64), (1, 24), (2, 115)]

CondensedNearestNeighbour 对噪声敏感，可能会添加噪声样本（见后面的图）。

3.2.2.3.1. 单边选择#

为了去除由CondensedNearestNeighbour引入的噪声观测，OneSidedSelection首先会找到难以分类的观测，然后使用TomekLinks去除噪声样本[Har68]。OneSidedSelection的运行方式如下：

获取集合 \(C\) 中的所有少数样本。
在目标类别（需要欠采样的类别）中添加一个样本，并将该类别中的所有其他样本放入集合 \(S\) 中。
在 \(C\) 上训练一个1-最近邻模型。
使用在3中训练的1最近邻规则，对集合\(S\)中的所有样本进行分类。
将所有错误分类的样本添加到 \(C\)。
从\(C\)中移除Tomek链接。

最终的数据集是\(S\)，包含来自少数类别的所有观察值，加上随机添加的多数类别的观察值，再加上所有被1-最近邻算法错误分类的多数类别的观察值。

请注意，与CondensedNearestNeighbour不同，OneSidedSelection 不会在每个样本被错误分类后训练K-最近邻。它使用步骤3中的1-最近邻在一次遍历中分类所有多数类样本。该类可以如下使用：

>>> from imblearn.under_sampling import OneSidedSelection
>>> oss = OneSidedSelection(random_state=0)
>>> X_resampled, y_resampled = oss.fit_resample(X, y)
>>> print(sorted(Counter(y_resampled).items()))
[(0, 64), (1, 174), (2, 4404)]

我们的实现提供了通过参数n_seeds_S设置随机放入集合\(C\)中的观测数量的可能性。

NeighbourhoodCleaningRule 将专注于清理数据而不是压缩它们 [Lau01]。因此，它将使用 EditedNearestNeighbours 和 3 最近邻分类器输出之间的样本联合来拒绝样本。该类可以如下使用：

>>> from imblearn.under_sampling import NeighbourhoodCleaningRule
>>> ncr = NeighbourhoodCleaningRule(n_neighbors=11)
>>> X_resampled, y_resampled = ncr.fit_resample(X, y)
>>> print(sorted(Counter(y_resampled).items()))
[(0, 64), (1, 193), (2, 4535)]

_images/sphx_glr_plot_comparison_under_sampling_005.png

3.2.3. 额外的欠采样技术#

3.2.3.1. 实例硬度阈值#

实例硬度是衡量正确分类一个实例或观察值的难易程度的指标。换句话说，硬实例是难以正确分类的观察值。

从根本上说，难以正确分类的实例是那些学习算法或分类器预测正确类标签概率较低的实例。

如果我们从数据集中移除这些难以处理的实例，逻辑上，我们将帮助分类器更好地识别不同的类别 [SMGC14]。

InstanceHardnessThreshold 在数据上训练一个分类器，然后移除概率较低的样本 [SMGC14]。换句话说，它保留了具有较高类别概率的观测值。

在我们的实现中，InstanceHardnessThreshold 几乎是一种受控的下采样方法：它将保留目标类别的特定数量的观察值，这是由用户指定的（见下面的注意事项）。

该类可以用作：

>>> from sklearn.linear_model import LogisticRegression
>>> from imblearn.under_sampling import InstanceHardnessThreshold
>>> iht = InstanceHardnessThreshold(random_state=0,
...                                 estimator=LogisticRegression())
>>> X_resampled, y_resampled = iht.fit_resample(X, y)
>>> print(sorted(Counter(y_resampled).items()))
[(0, 64), (1, 64), (2, 64)]

InstanceHardnessThreshold 有2个重要参数。参数 estimator 接受任何具有 predict_proba 方法的 scikit-learn 分类器。该分类器将用于识别困难实例。训练是通过交叉验证进行的，可以通过参数 ``cv` 指定。

注意

InstanceHardnessThreshold 几乎可以被视为一种受控的欠采样方法。然而，由于概率输出，它并不总是能够获得指定数量的样本。

下图展示了一个玩具数据集上的实例硬度欠采样示例。

_images/sphx_glr_plot_comparison_under_sampling_006.png