隐马尔可夫模型

作者: Jacob Schreiber 联系方式: jmschreiber91@gmail.com

隐马尔可夫模型（HMMs）是一种针对序列的概率分布，由两个组成部分构成：一组概率分布和一个描述序列如何在模型中演进的转移矩阵（有时以图的形式表示）。HMMs是pomegranate中的旗舰实现，也是最初实现的第一个算法。

隐马尔可夫模型(HMMs)是一种结构化预测方法，常用于为序列中的所有元素标注某种"隐藏"状态。可以将其视为马尔可夫链的扩展形式，不同之处在于：不是下一个观测值的概率取决于当前观测值，而是下一个隐藏状态的概率取决于当前隐藏状态，而下一个观测值则源自该隐藏状态。词性标注就是这种模型的一个应用实例，其中观测值是单词，隐藏状态是词性。每个单词都会被标注一个词性，但系统会利用动态编程算法搜索所有可能的单词-标签组合，以确定整个句子中最优的标签集。

%pylab inline
import seaborn; seaborn.set_style('whitegrid')

import torch

numpy.random.seed(0)
numpy.set_printoptions(suppress=True)

%load_ext watermark
%watermark -m -n -p numpy,scipy,torch,pomegranate

Populating the interactive namespace from numpy and matplotlib
numpy      : 1.23.4
scipy      : 1.9.3
torch      : 1.13.0
pomegranate: 1.0.0

Compiler    : GCC 11.2.0
OS          : Linux
Release     : 4.15.0-208-generic
Machine     : x86_64
Processor   : x86_64
CPU cores   : 8
Architecture: 64bit

基因组中GC富集区域的识别

让我们以DNA序列上CG岛检测的简化示例来说明。DNA由四种标准核苷酸组成，缩写为'A'、'C'、'G'和'T'。我们可以说基因组中富含'C'和'G'核苷酸的区域是'CG岛'，这是对真实生物学概念的简化，但对于我们的示例已经足够。识别这些区域的难点在于它们并非完全由'C'和'G'核苷酸组成，而是混杂着一些'A'和'T'。如果使用简单的模型来寻找连续的C和G长片段，效果会很差，因为它会漏掉大多数真实区域。

我们可以从构建模型开始。由于隐马尔可夫模型(HMM)涉及转移矩阵，而转移矩阵通常用隐藏状态上的图来表示，因此构建它们比简单的分布或混合模型需要更多步骤。我们的简单模型将由两个分布组成。一个分布将是所有四个字符上的均匀分布，另一个分布将偏好核苷酸C和G，同时仍允许核苷酸A和T存在。

from pomegranate.distributions import Categorical

d1 = Categorical([[0.25, 0.25, 0.25, 0.25]])
d2 = Categorical([[0.10, 0.40, 0.40, 0.10]])

现在我们可以定义HMM并传入状态。请注意在pomegranate v1.0.0中，HMM被分为两种实现：DenseHMM（具有密集转移矩阵，因此可以在后端使用标准矩阵乘法）和SparseHMM（具有稀疏转移矩阵并使用更复杂的分散-加法操作）。另外请注意，您不再需要将分布包装在Node对象中，而是可以直接传入分布。

from pomegranate.hmm import DenseHMM

model = DenseHMM()
model.add_distributions([d1, d2])

接下来我们需要定义转移矩阵，它表示从一个隐藏状态转移到下一个隐藏状态的概率。在某些情况下（比如本例），自循环概率较高，这意味着在序列中从一个观测到下一个观测时，很可能保持相同的隐藏状态。其他情况（如词性标注器）则保持相同状态的概率较低。转移矩阵的一部分是初始概率，即从各个隐藏状态开始的概率。由于我们每次只创建一个转移，因此非常适合使用稀疏转移矩阵——即某些隐藏状态之间不可能发生转移。请注意，这里我们传入的是分布对象，而非之前版本中的节点对象。

model.add_edge(model.start, d1, 0.5)
model.add_edge(model.start, d2, 0.5)
model.add_edge(d1, d1, 0.9)
model.add_edge(d1, d2, 0.1)
model.add_edge(d2, d1, 0.1)
model.add_edge(d2, d2, 0.9)

另一个重大变化是，一旦完成，我们不再需要预先构建HMM！

#model.bake()

现在我们可以创建一个序列来运行模型。确保该序列已转换为类别的数值表示形式。这可以简单地完成，如下所示，或者使用其他包（如scikit-learn）中的预处理工具。另外，请确保输入序列是三维的，三个维度分别对应（批次大小、序列长度、维度）。这里，批次大小和维度均为1。当并行处理多个序列时，包含批次大小会显著提升效率。

sequence = 'CGACTACTGACTACTCGCCGACGCGACTGCCGTCTATACTGCGCATACGGC'
X = numpy.array([[[['A', 'C', 'G', 'T'].index(char)] for char in sequence]])
X.shape

(1, 51, 1)

现在我们可以对某些序列进行预测。让我们创建一个中间含有CG富集区域的序列，看看是否能识别出来。

y_hat = model.predict(X)

print("sequence: {}".format(''.join(sequence)))
print("hmm pred: {}".format(''.join([str(y.item()) for y in y_hat[0]])))

sequence: CGACTACTGACTACTCGCCGACGCGACTGCCGTCTATACTGCGCATACGGC
hmm pred: 000000000000000111111111111111100000000000000001111

看起来它成功识别了中间的一个CG岛（那一段连续的1）以及末尾另一个较短的CG岛。更重要的是，模型没有被误导认为每个CG甚至成对的CG都是岛屿。它需要许多C和G组成较长片段才能将该区域识别为岛屿。当然，转移概率和发射概率的平衡会极大影响检测到的区域范围。

假设我们想要去掉末尾那个CG岛预测，因为我们不认为真实岛屿会出现在序列末端。我们可以通过添加一个显式结束状态来解决这个问题，该状态只能由非岛屿隐藏状态到达。我们强制模型必须在结束状态终止，如果只有非岛屿状态能到达该状态，那么隐藏状态序列最终必定以非岛屿状态结束。具体实现如下：

model = DenseHMM()
model.add_distributions([d1, d2])
model.add_edge(model.start, d1, 0.5)
model.add_edge(model.start, d2, 0.5)
model.add_edge(d1, d1, 0.89 )
model.add_edge(d1, d2, 0.10 )
model.add_edge(d1, model.end, 0.01)
model.add_edge(d2, d1, 0.1 )
model.add_edge(d2, d2, 0.9)

请注意，我们只是添加了一个从n1到model.end的低概率转移。如果那里只有一个转移，这个概率不需要很高，因为没有其他可能到达结束状态的方式。

y_hat = model.predict(X)

print("sequence: {}".format(''.join(sequence)))
print("hmm pred: {}".format(''.join([str(y.item()) for y in y_hat[0]])))

sequence: CGACTACTGACTACTCGCCGACGCGACTGCCGTCTATACTGCGCATACGGC
hmm pred: 000000000000000111111111111111100000000000000000000

这看起来合理多了。有一个单独的CG岛被背景序列包围，末端还有一些东西。如果我们知道CG岛不可能出现在序列末端，只需修改HMM的基础结构就能规定序列必须从背景状态结束。

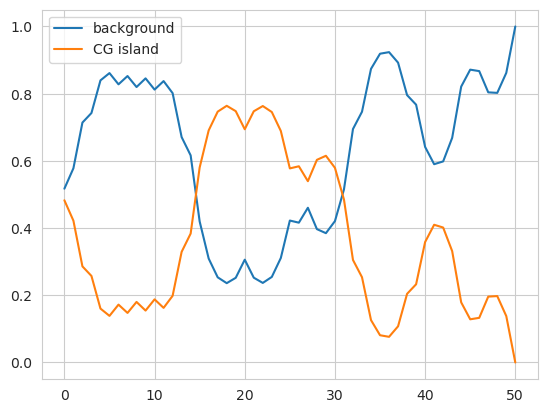
就像混合模型可以提供类分配的概率估计而不仅仅是硬标签一样，隐马尔可夫模型也能做到这一点。这些估计值是在给定观测值的情况下属于每个隐藏状态的后验概率，同时也考虑了序列的其余部分。

plt.plot(model.predict_proba(X)[0], label=['background', 'CG island'])
plt.legend()
plt.show()

我们可以看到这里从第一个非岛屿区域到中间岛屿区域的转变，其中一列的高概率转变为另一列的高概率。predict方法只是选择最可能的元素——即最大后验估计。

除了使用前向-后向算法仅计算每个观测值的后验概率外，我们还可以统计预测中每条边上发生的转移次数。

transitions = model.forward_backward(X)[0][0]
transitions

tensor([[28.9100,  2.4128],
        [ 2.8955, 15.7806]])

初始化隐马尔可夫模型

有两种方法可以使用pomegranate初始化HMM。第一种是显式传递一个分布列表、一个密集的转移矩阵，以及可选的起始和结束概率。我们可以使用这种方法重建上述模型。

model = DenseHMM([d1, d2], edges=[[0.89, 0.1], [0.1, 0.9]], starts=[0.5, 0.5], ends=[0.01, 0.0])

我们可以通过绘制序列上预测概率的相同图表来验证这种初始化是否产生了相同的模型。

plt.plot(model.predict_proba(X)[0], label=['background', 'CG island'])
plt.legend()
plt.show()

在创建SparseHMM对象时同样适用，不过边必须是一个三元组列表而非矩阵。

from pomegranate.hmm import SparseHMM

edges = [
    [d1, d1, 0.89],
    [d1, d2, 0.1],
    [d2, d1, 0.1],
    [d2, d2, 0.9]
]

model = SparseHMM([d1, d2], edges=edges, starts=[0.5, 0.5], ends=[0.01, 0.0])

plt.plot(model.predict_proba(X)[0], label=['background', 'CG island'])
plt.legend()
plt.show()

第二种方法是按照上述步骤，首先创建一个未初始化的模型，不传入任何参数，然后使用适当的方法添加分布和边。虽然这适用于DenseHMM和SparseHMM模型，但对于非常稀疏的SparseHMM模型或需要基于外部因素程序化生成HMM的情况最为实用。以下是使用这种方法实现HMM的相同代码。

model = SparseHMM()
model.add_distributions([d1, d2])
model.add_edge(model.start, d1, 0.5)
model.add_edge(model.start, d2, 0.5)
model.add_edge(d1, d1, 0.89 )
model.add_edge(d1, d2, 0.10 )
model.add_edge(d1, model.end, 0.01)
model.add_edge(d2, d1, 0.1 )
model.add_edge(d2, d2, 0.9)

与其他方法类似，我们可以创建一个具有未初始化分布的HMM。这些分布将在提供数据时使用k-means聚类进行初始化。当使用DenseHMM时，我们还可以选择不传入边，并将其初始化为均匀概率。当使用SparseHMM时，我们必须传入边，否则模型将不知道哪些边存在，哪些不存在。本质上，它也不得不假设均匀概率，此时模型将具有密集的转移矩阵，但通过将其视为稀疏矩阵来低效运行。

from pomegranate.distributions import Normal

X3 = torch.randn(100, 50, 2)

model3 = DenseHMM([Normal(), Normal(), Normal()], verbose=True)
model3._initialize(X3)
model3.distributions[0].means, model3.distributions[1].means, model3.distributions[2].means

(Parameter containing:
 tensor([-0.6929,  0.2710]),
 Parameter containing:
 tensor([1.0994, 0.7262]),
 Parameter containing:
 tensor([ 0.4207, -1.0267]))

您可以通过向init传入值来控制k-means本身的初始化方式。

不过，您无需手动初始化模型。如果调用fit方法或summarize方法，这些分布将在尚未初始化时自动完成初始化。

X3 = torch.randn(100, 50, 2)

model3 = DenseHMM([Normal(), Normal(), Normal()], max_iter=5, verbose=True)
model3.fit(X3)

[1] Improvement: -23.134765625, Time: 0.007689s

DenseHMM(
  (start): Silent()
  (end): Silent()
  (distributions): ModuleList(
    (0): Normal()
    (1): Normal()
    (2): Normal()
  )
)

密集与稀疏隐马尔可夫模型

除了HMM是通过初始传入分布和边还是通过编程构建模型来初始化之外，转移矩阵可以使用稀疏矩阵或稠密矩阵来表示。虽然稠密转移矩阵允许每个算法使用快速矩阵乘法，但一旦零值足够多，矩阵乘法在处理它们时会浪费大量计算资源。

由于初始化模型的后端和策略（即传入密集转移矩阵或边列表）有所不同，pomegranate v1.0.0将实现分为两种：DenseHMM 和 SparseHMM。两者具有相同的功能和API接口，在给定相同转移矩阵的情况下会产生相同的结果。

edges = [[0.89, 0.1], [0.1, 0.9]]
starts = [0.5, 0.5]
ends = [0.01, 0.0]

model1 = DenseHMM([d1, d2], edges=edges, starts=starts, ends=ends)
model1.predict_proba(X)[0][12:19]

tensor([[0.8016, 0.1984],
        [0.6708, 0.3292],
        [0.6163, 0.3837],
        [0.4196, 0.5804],
        [0.3092, 0.6908],
        [0.2535, 0.7465],
        [0.2361, 0.7639]])

edges = [
    [d1, d1, 0.89],
    [d1, d2, 0.1],
    [d2, d1, 0.1],
    [d2, d2, 0.9]
]

model2 = SparseHMM([d1, d2], edges=edges, starts=starts, ends=ends)
model2.predict_proba(X)[0][12:19]

tensor([[0.8016, 0.1984],
        [0.6708, 0.3292],
        [0.6163, 0.3837],
        [0.4196, 0.5804],
        [0.3092, 0.6908],
        [0.2535, 0.7465],
        [0.2361, 0.7639]])

X = numpy.random.choice(4, size=(1000, 500, 1))

%timeit -n 10 -r 5 model1.predict_proba(X)
%timeit -n 10 -r 5 model2.predict_proba(X)

102 ms ± 13.9 ms per loop (mean ± std. dev. of 5 runs, 10 loops each)
177 ms ± 12.9 ms per loop (mean ± std. dev. of 5 runs, 10 loops each)

查看基准测试文件夹以获取两者更全面的对比，但看起来即使是小型模型，密集转移矩阵的速度也大约快两倍。

隐马尔可夫模型拟合

隐马尔可夫模型通常使用Baum-Welch算法拟合未标记数据。这是一种结构化EM算法，不仅考虑分布参数本身，还考虑了分布之间的转移。本质上，我们使用前向-后向算法来推断每条边上的预期转移次数以及每个观测值对应每个状态的预期概率，然后利用这些估计值来更新底层参数。

d1 = Categorical([[0.25, 0.25, 0.25, 0.25]])
d2 = Categorical([[0.10, 0.40, 0.40, 0.10]])

edges = [[0.89, 0.1], [0.1, 0.9]]
starts = [0.5, 0.5]
ends = [0.01, 0.0]

model = DenseHMM([d1, d2], edges=edges, starts=starts, ends=ends, verbose=True)
model.fit(X)

[1] Improvement: 16405.125, Time: 0.09408s
[2] Improvement: 420.75, Time: 0.0876s
[3] Improvement: 207.25, Time: 0.09545s
[4] Improvement: 116.125, Time: 0.107s
[5] Improvement: 75.3125, Time: 0.09284s
[6] Improvement: 47.6875, Time: 0.0797s
[7] Improvement: 34.75, Time: 0.1045s
[8] Improvement: 27.3125, Time: 0.08161s
[9] Improvement: 16.0625, Time: 0.08903s
[10] Improvement: 15.6875, Time: 0.1197s
[11] Improvement: 9.1875, Time: 0.09623s
[12] Improvement: 10.625, Time: 0.08911s
[13] Improvement: 8.125, Time: 0.1064s
[14] Improvement: 6.3125, Time: 0.07936s
[15] Improvement: 2.3125, Time: 0.08887s
[16] Improvement: 5.0625, Time: 0.108s
[17] Improvement: 4.3125, Time: 0.08656s
[18] Improvement: 3.1875, Time: 0.08103s
[19] Improvement: 1.75, Time: 0.1282s
[20] Improvement: 4.4375, Time: 0.09025s
[21] Improvement: -1.6875, Time: 0.07991s

DenseHMM(
  (start): Silent()
  (end): Silent()
  (distributions): ModuleList(
    (0): Categorical()
    (1): Categorical()
  )
)

我们可以通过设置max_iter参数或tol参数来改变迭代次数。

d1 = Categorical([[0.25, 0.25, 0.25, 0.25]])
d2 = Categorical([[0.10, 0.40, 0.40, 0.10]])

edges = [[0.89, 0.1], [0.1, 0.9]]
starts = [0.5, 0.5]
ends = [0.01, 0.0]

model = DenseHMM([d1, d2], edges=edges, starts=starts, ends=ends, max_iter=5, verbose=True)
model.fit(X)

[1] Improvement: 16405.125, Time: 0.1029s
[2] Improvement: 420.75, Time: 0.1356s
[3] Improvement: 207.25, Time: 0.1192s
[4] Improvement: 116.125, Time: 0.08874s
[5] Improvement: 75.3125, Time: 0.1781s

DenseHMM(
  (start): Silent()
  (end): Silent()
  (distributions): ModuleList(
    (0): Categorical()
    (1): Categorical()
  )
)

d1 = Categorical([[0.25, 0.25, 0.25, 0.25]])
d2 = Categorical([[0.10, 0.40, 0.40, 0.10]])

edges = [[0.89, 0.1], [0.1, 0.9]]
starts = [0.5, 0.5]
ends = [0.01, 0.0]

model = DenseHMM([d1, d2], edges=edges, starts=starts, ends=ends, tol=50, verbose=True)
model.fit(X)

[1] Improvement: 16405.125, Time: 0.1512s
[2] Improvement: 420.75, Time: 0.1788s
[3] Improvement: 207.25, Time: 0.1501s
[4] Improvement: 116.125, Time: 0.127s
[5] Improvement: 75.3125, Time: 0.08657s
[6] Improvement: 47.6875, Time: 0.1011s

DenseHMM(
  (start): Silent()
  (end): Silent()
  (distributions): ModuleList(
    (0): Categorical()
    (1): Categorical()
  )
)

相同的参数和签名适用于SparseHMM模型。