分布式自动求导设计

本笔记将介绍分布式自动求导的详细设计，并深入探讨其内部机制。在继续之前，请确保您熟悉自动求导机制和分布式RPC框架。

背景

假设你有两个节点和一个非常简单的模型分布在两个节点上。这可以使用torch.distributed.rpc来实现，如下所示：

import torch
import torch.distributed.rpc as rpc

def my_add(t1, t2):
  return torch.add(t1, t2)

# 在 worker 0 上：
t1 = torch.rand((3, 3), requires_grad=True)
t2 = torch.rand((3, 3), requires_grad=True)

# 在远程执行一些计算。
t3 = rpc.rpc_sync("worker1", my_add, args=(t1, t2))

# 基于远程结果在本地执行一些计算。
t4 = torch.rand((3, 3), requires_grad=True)
t5 = torch.mul(t3, t4)

# 计算一些损失。
loss = t5.sum()

分布式自动梯度的主要动机是能够在这种分布式模型上运行反向传播，使用我们计算的损失，并为所有需要梯度的张量记录适当的梯度。

前向传播过程中的自动梯度记录

PyTorch 在前向传播过程中构建自动求导图，并使用该图执行反向传播。更多详情请参见 自动求导如何编码历史。

对于分布式自动求导，我们需要在正向传递过程中跟踪所有RPC，以确保反向传递能够正确执行。为此，我们在执行RPC时将send和recv函数附加到自动求导图中。

• 函数 send 附加到 RPC 的源，其输出边指向 RPC 输入张量的 autograd 函数。 在反向传播过程中，该函数的输入从目标接收，作为适当 recv 函数的输出。

• 函数 recv 被附加到RPC的目标端，其输入是从在目标端执行的运算符中获取的输入张量。在反向传播过程中，该函数的输出梯度会被发送到源节点，并传递给相应的 send 函数。

• 每个send-recv对都被分配了一个全局唯一的autograd_message_id，以唯一标识该对。这在反向传播过程中查找远程节点上的相应函数时非常有用。

• 对于RRef，每当我们调用torch.distributed.rpc.RRef.to_here() 时，我们会为涉及的张量附加适当的send-recv对。

作为一个例子，这是我们上面例子的自动梯度图的样子（为了简单起见，排除了t5.sum()）：

分布式自动求导上下文

每个使用分布式自动求导的前向和后向传递都会被分配一个唯一的 torch.distributed.autograd.context，并且这个上下文具有全局唯一的 autograd_context_id。这个上下文会在每个节点上根据需要创建。

此上下文用于以下目的：

1. 多个节点运行分布式反向传播可能会在同一个张量上累积梯度，结果是张量的 .grad 字段会在我们有机会运行优化器之前，从各种分布式反向传播中累积梯度。这类似于在本地多次调用 torch.autograd.backward()。为了提供一种分离每次反向传播梯度的方法，梯度会在每次反向传播的 torch.distributed.autograd.context 中累积。

2. 在前向传播过程中，我们在这个上下文中存储每个自动求导过程的send和recv函数。这确保我们持有自动求导图中适当节点的引用，以保持其活跃状态。此外，在反向传播过程中，可以轻松查找适当的send和recv函数。

3. 通常我们也会使用这个上下文来存储每个分布式自动求导过程的一些元数据。

从用户的角度来看，autograd 上下文的设置如下：

import torch.distributed.autograd as dist_autograd
with dist_autograd.context() as context_id:
  loss = model.forward()
  dist_autograd.backward(context_id, loss)

需要注意的是，必须在分布式自动求导上下文管理器中调用模型的前向传播，因为需要一个有效的上下文来确保所有send和recv函数都能被正确存储，以便在所有参与节点上运行反向传播。

分布式反向传播

在本节中，我们概述了在分布式反向传播过程中准确计算依赖关系的挑战，并描述了几种算法（带有权衡），说明我们如何执行分布式反向传播。

计算依赖关系

考虑以下在单台机器上运行的代码片段

import torch
a = torch.rand((3, 3), requires_grad=True)
b = torch.rand((3, 3), requires_grad=True)
c = torch.rand((3, 3), requires_grad=True)
d = a + b
e = b * c
d.sum.().backward()

这是上述代码的自动梯度图的样子：

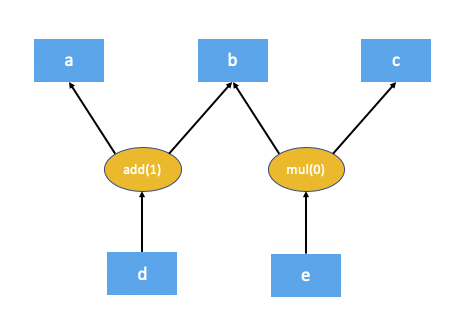
反向传播过程中，autograd引擎执行的第一步是计算autograd图中每个节点的依赖项数量。这有助于autograd引擎知道图中的节点何时准备好执行。add(1)和mul(0)括号中的数字表示依赖项的数量。如您所见，这意味着在反向传播过程中，add节点需要1个输入，而mul节点不需要任何输入（换句话说，不需要执行）。本地autograd引擎通过从根节点（在本例中为d）遍历图来计算这些依赖项。

在 autograd 图中某些节点可能不会在反向传播中执行，这对分布式 autograd 提出了挑战。考虑以下使用 RPC 的代码片段。

import torch
import torch.distributed.rpc as rpc

a = torch.rand((3, 3), requires_grad=True)
b = torch.rand((3, 3), requires_grad=True)
c = torch.rand((3, 3), requires_grad=True)

d = rpc.rpc_sync("worker1", torch.add, args=(a, b))
e = rpc.rpc_sync("worker1", torch.mul, args=(b, c))
loss = d.sum()

上述代码的关联自动求导图将是：

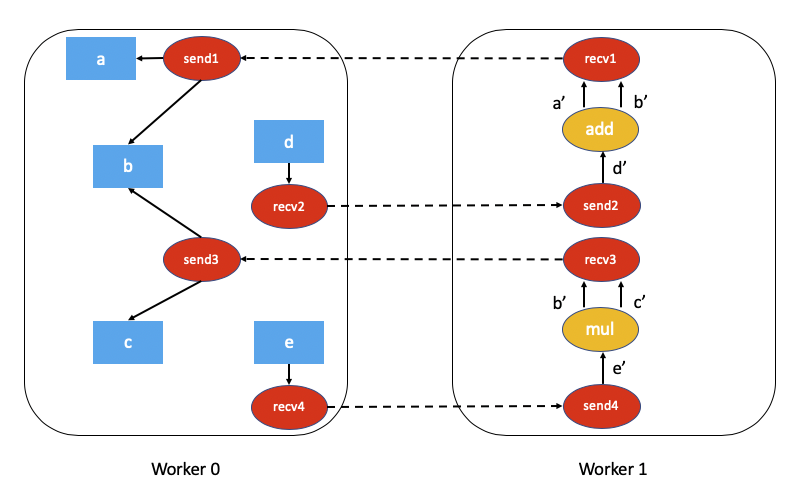
计算这个分布式自动求导图的依赖关系要困难得多，并且需要一些开销（无论是计算还是网络通信）。

对于性能敏感的应用程序，我们可以通过假设每个send和recv函数在反向传播过程中都是有效的（大多数应用程序不会执行未使用的RPC）来避免大量开销。这简化了分布式自动求导算法，并且效率更高，但代价是应用程序需要了解其局限性。该算法称为快速模式算法，并在下面详细描述。

在一般情况下，并非每个send和recv函数都必须作为反向传播的一部分有效。为了解决这个问题，我们提出了一种SMART模式算法，该算法将在后面的部分中描述。请注意，目前仅实现了FAST模式算法。

FAST模式算法

该算法的关键假设是，当我们运行反向传播时，每个 send 函数都有一个依赖性为1。换句话说，我们假设我们将从另一个节点通过RPC接收到一个梯度。

算法如下：

1. 我们从具有反向传播根节点的worker开始（所有根节点必须是本地的）。

2. 查找当前分布式自动求导上下文的所有send函数。

3. 从提供的根节点和所有我们检索到的send函数开始，在本地计算依赖关系。

4. 在计算依赖关系后，使用提供的根节点启动本地自动求导引擎。

5. 当 autograd 引擎执行 recv 函数时，recv 函数通过 RPC 将输入梯度发送到适当的 worker。 每个 recv 函数都知道目标 worker 的 ID，因为它作为前向传播的一部分被记录下来。recv 函数还会将 autograd_context_id 和 autograd_message_id 发送到远程主机。

6. 当在远程主机上接收到此请求时，我们使用 autograd_context_id 和 autograd_message_id 来查找 适当的 send 函数。

7. 如果这是工作者首次收到针对给定 autograd_context_id的请求，它将按照上述第1-3点所述在本地计算依赖关系。

8. 在第6步中获取的send函数随后被排队等待在该工作者的本地自动求导引擎上执行。

9. 最后，我们不是在 .grad 字段上累积梯度，而是根据每个 分布式自动求导上下文 单独累积梯度。梯度存储在一个 Dict[Tensor, Tensor] 中，这基本上是一个从张量到其相关梯度的映射，可以使用 get_gradients() API 检索此映射。

作为一个例子，完整的代码与分布式自动梯度如下：

import torch
import torch.distributed.autograd as dist_autograd
import torch.distributed.rpc as rpc

def my_add(t1, t2):
  return torch.add(t1, t2)

# 在 worker 0 上：

# 设置自动求导上下文。参与分布式反向传播的计算必须在分布式自动求导上下文管理器内进行。
with dist_autograd.context() as context_id:
  t1 = torch.rand((3, 3), requires_grad=True)
  t2 = torch.rand((3, 3), requires_grad=True)

  # 在远程执行一些计算。
  t3 = rpc.rpc_sync("worker1", my_add, args=(t1, t2))

  # 基于远程结果在本地执行一些计算。
  t4 = torch.rand((3, 3), requires_grad=True)
  t5 = torch.mul(t3, t4)

  # 计算一些损失。
  loss = t5.sum()

  # 运行反向传播。
  dist_autograd.backward(context_id, [loss])

  # 从上下文中检索梯度。
  dist_autograd.get_gradients(context_id)

具有依赖关系的分布式自动求导图如下所示（为简单起见，排除了t5.sum()）：

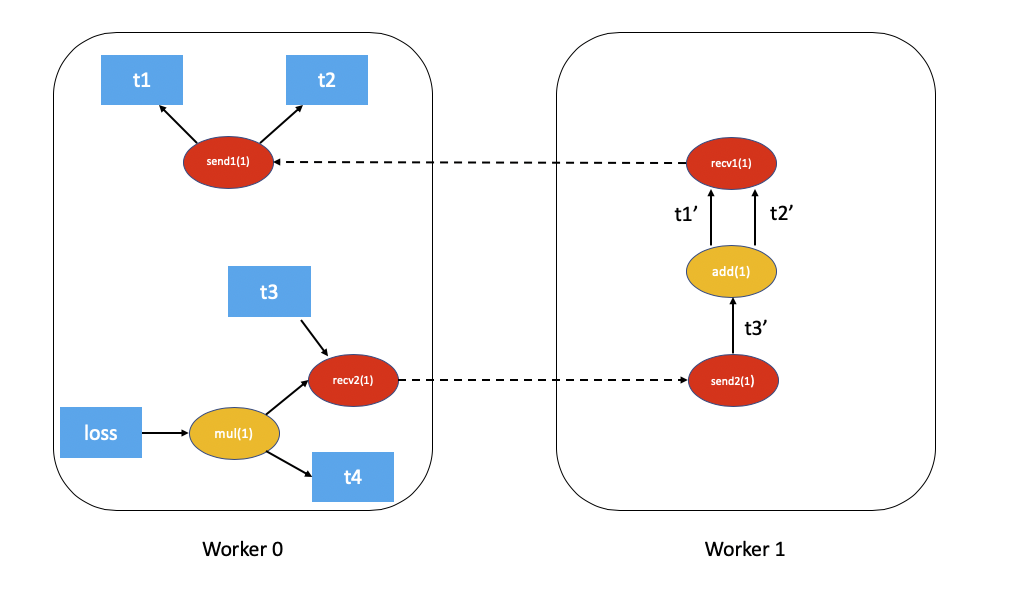
应用于上述示例的FAST模式算法如下：

1. 在Worker 0上，我们从根节点loss和send1开始计算依赖关系。结果是send1被标记为具有1的依赖关系，而mul在Worker 0上被标记为具有1的依赖关系。

2. 现在，我们在Worker 0上启动本地自动微分引擎。我们首先执行 mul函数，将其输出累积在自动微分上下文中作为 t4的梯度。然后，我们执行recv2，将梯度发送给 Worker 1。

3. 由于这是Worker 1第一次听说这个反向传播， 它开始依赖计算并适当地标记send2、 add和recv1的依赖关系。

4. 接下来，我们在Worker 1的本地自动求导引擎上将send2加入队列，这反过来执行add和recv1。

5. 当执行recv1时，它会将梯度发送给Worker 0。

6. 由于Worker 0已经为此反向传播计算了依赖关系， 它只需在本地排队并执行send1。

7. 最后，t1、t2 和 t4 的梯度在 分布式自动求导上下文中累积。

SMART模式算法

该算法的详细信息仍在完善中，但您可以参考RFC中的分布式自动求导算法智能模式部分以了解大致思路。

分布式优化器

The DistributedOptimizer 操作如下：

1. 接受一个远程参数列表（RRef）进行优化。这些参数也可以是包装在本地RRef中的本地参数。

2. 将一个 Optimizer 类作为本地优化器，在所有不同的 RRef 所有者上运行。

3. 分布式优化器在每个工作节点上创建一个本地 Optimizer 实例，并持有它们的 RRef。

4. 当调用torch.distributed.optim.DistributedOptimizer.step()时， 分布式优化器使用RPC在适当的远程工作节点上远程执行所有本地优化器。必须提供一个分布式自动求导 context_id作为输入给 torch.distributed.optim.DistributedOptimizer.step()。本地优化器使用它来应用存储在相应上下文中的梯度。

5. 如果多个并发分布式优化器正在更新同一个工作节点上的参数，这些更新将通过锁进行序列化。

简单的端到端示例

将所有内容整合在一起，以下是一个使用分布式自动梯度和分布式优化器的简单端到端示例。如果将代码放入名为“dist_autograd_simple.py”的文件中，可以使用以下命令运行：

MASTER_ADDR="localhost" MASTER_PORT=29500 python dist_autograd_simple.py

import torch
import torch.multiprocessing as mp
import torch.distributed.autograd as dist_autograd
from torch.distributed import rpc
from torch import optim
from torch.distributed.optim import DistributedOptimizer

def random_tensor():
    return torch.rand((3, 3), requires_grad=True)

def _run_process(rank, dst_rank, world_size):
    name = "worker{}".format(rank)
    dst_name = "worker{}".format(dst_rank)

    # 初始化RPC。
    rpc.init_rpc(
        name=name,
        rank=rank,
        world_size=world_size
    )

    # 使用分布式自动求导上下文。
    with dist_autograd.context() as context_id:
        # 前向传播（在远程节点上创建引用）。
        rref1 = rpc.remote(dst_name, random_tensor)
        rref2 = rpc.remote(dst_name, random_tensor)
        loss = rref1.to_here() + rref2.to_here()

        # 反向传播（运行分布式自动求导）。
        dist_autograd.backward(context_id, [loss.sum()])

        # 构建分布式优化器。
        dist_optim = DistributedOptimizer(
        optim.SGD,
        [rref1, rref2],
        lr=0.05,
        )

        # 运行分布式优化器步骤。
        dist_optim.step(context_id)

def run_process(rank, world_size):
    dst_rank = (rank + 1) % world_size
    _run_process(rank, dst_rank, world_size)
    rpc.shutdown()

if __name__ == '__main__':
  # 运行world_size个工作进程
  world_size = 2
  mp.spawn(run_process, args=(world_size,), nprocs=world_size)