使用适配器

简介

您可以定义适配器来在优化过程中实现动态变异和交叉概率，而非固定值。其理念是将这些概率设为世代数的函数；这种定义可以实现不同的训练策略，例如：

开始时采用较高的变异概率以探索更多样化的解决方案，然后逐步降低变异概率，专注于保留更有潜力的解。
初始使用较低交叉概率，最终采用较高概率
为每个参数组合不同的策略

所有方法都使用三个参数：

initial_value: 这是在第0代时使用的初始值
end_value: 这是参数从initial_value开始可以取到的极限值
adaptive_rate: 控制数值接近end_value的速度；数值越大收敛速度越快

在接下来的章节中，理解以下符号表示非常重要：

名称	符号
初始值	\(p_0\)
终止值	\(p_f\)
当前世代	\(t\)
自适应率	\(\alpha\)
第t代的值	\(p(t; \alpha)\)

请注意 \(p_0\) 不需要大于 \(p_f\)。

如果 \(p_0 > p_f\)，则表示您正在向 \(p_f\) 进行衰减。

如果 \(p_0 < p_f\)，则表示您正在向 \(p_f\) 进行上升操作。

所有非常数适配器 \(p(t; \alpha)\)，当 \(\alpha \in (0,1)\) 时，具有以下特性：

\[\begin{split}\lim_{t->0^{+}} p(t; \alpha) = p_0\\ \\ \lim_{t->+\infty} p(t; \alpha) = p_f\end{split}\]

以下适配器可用：

常量适配器
指数适配器
反向适配器
潜在适配器

ConstantAdapter

该适配器旨在供包内部使用；当用户未创建适配器，而是将交叉或变异概率定义为实数时，包会将其转换为ConstantAdapter，以便库能在两种情况下使用相同方法调用内部API。因此，其定义为：

\[p(t; \alpha) = p_0\]

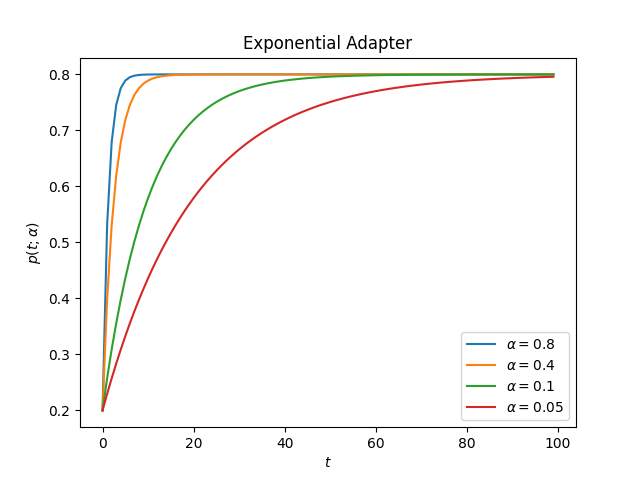
ExponentialAdapter

指数适配器使用以下形式来改变初始值

\[p(t; \alpha) = (p_0-p_f)e^{-\alpha t} + p_f\]

使用示例：

from sklearn_genetic.schedules import ExponentialAdapter

# Decay over initial_value
adapter = ExponentialAdapter(initial_value=0.8, end_value=0.2, adaptive_rate=0.1)

# Run a few iterations
for _ in range(3):
    adapter.step()  # 0.8, 0.74, 0.69

这是适配器在不同alpha值下的表现

衰减:

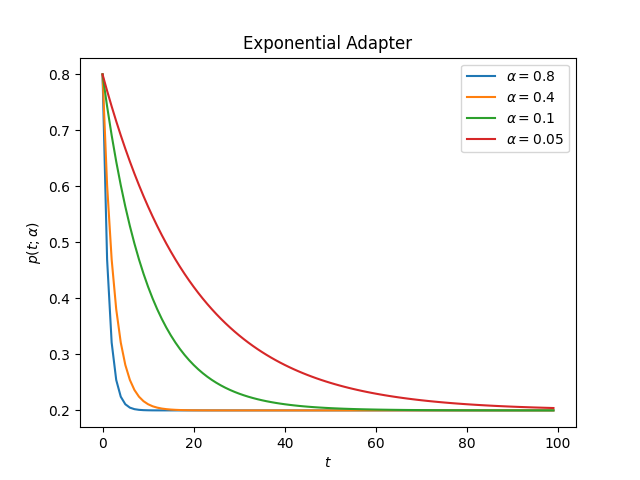
升序：

import matplotlib.pyplot as plt
from sklearn_genetic.schedules import ExponentialAdapter

values = [{"initial_value": 0.8, "end_value": 0.2},  # Decay
          {"initial_value": 0.2, "end_value": 0.8}]  # Ascend
alphas = [0.8, 0.4, 0.1, 0.05]

for value in values:
    for alpha in alphas:
        adapter = ExponentialAdapter(**value, adaptive_rate=alpha)
        adapter_result = [adapter.step() for _ in range(100)]

        plt.plot(adapter_result, label=r'$\alpha={}$'.format(alpha))

    plt.xlabel(r'$t$')
    plt.ylabel(r'$p(t; \alpha)$')
    plt.title("Exponential Adapter")
    plt.legend()
    plt.show()

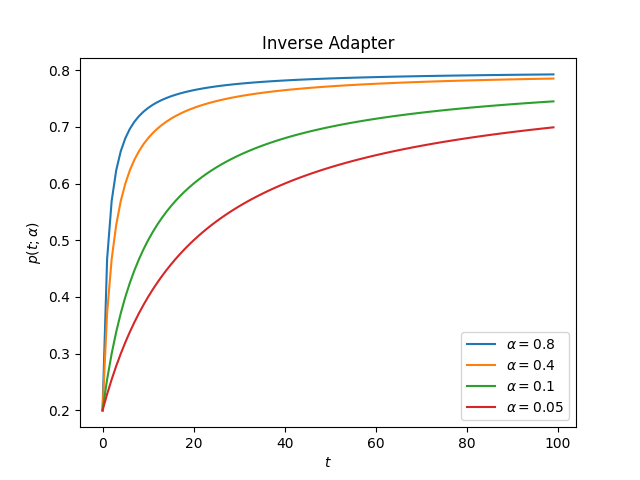
InverseAdapter

逆向适配器采用以下形式来改变初始值

\[p(t; \alpha) = \frac{(p_0-p_f)}{1+\alpha t} + p_f\]

使用示例：

from sklearn_genetic.schedules import InverseAdapter

# Decay over initial_value
adapter = InverseAdapter(initial_value=0.8, end_value=0.2, adaptive_rate=0.1)

# Run a few iterations
for _ in range(3):
    adapter.step()  # 0.8, 0.75, 0.7

这是适配器在不同alpha值下的表现

衰减:

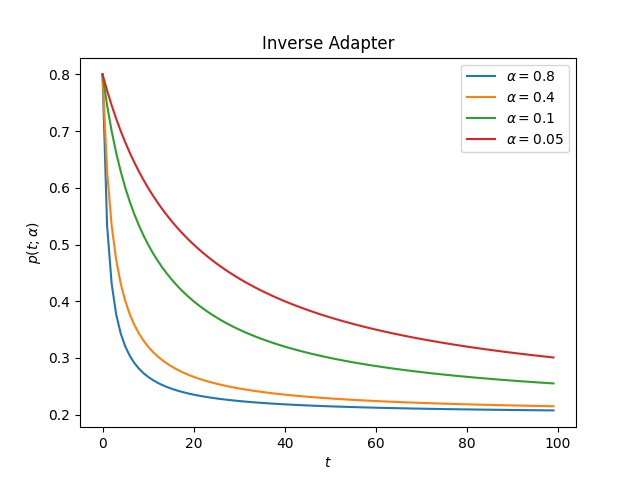
升序：

PotentialAdapter

逆向适配器采用以下形式来改变初始值

\[p(t; \alpha) = (p_0-p_f)(1-\alpha)^{ t} + p_f\]

使用示例：

from sklearn_genetic.schedules import PotentialAdapter

# Decay over initial_value
adapter = PotentialAdapter(initial_value=0.8, end_value=0.2, adaptive_rate=0.1)

# Run a few iterations
for _ in range(3):
    adapter.step()  # 0.8, 0.26, 0.206

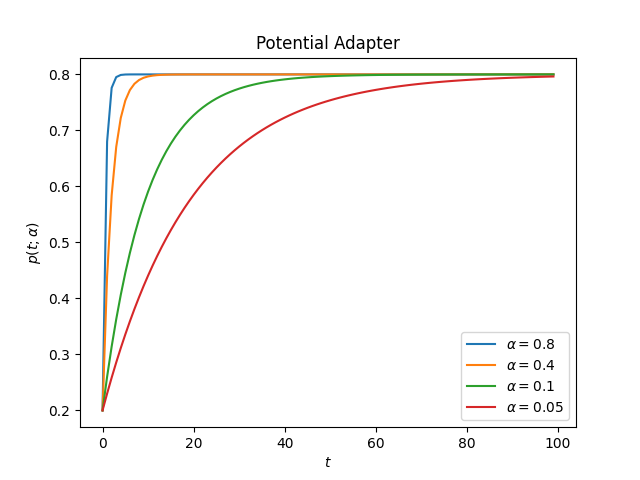
这是适配器在不同alpha值下的表现

衰减:

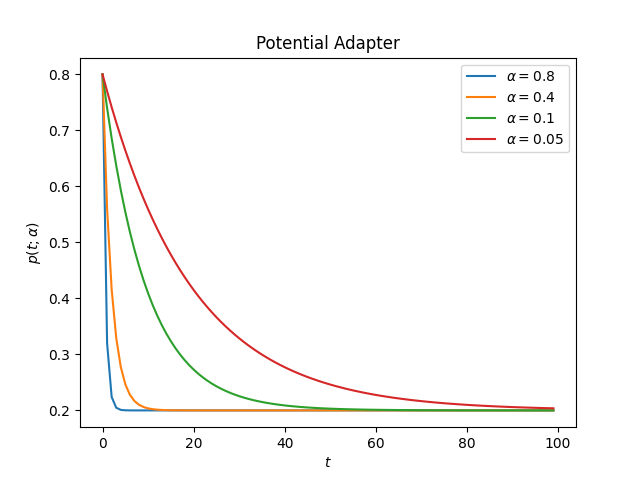
升序：

对比

这是所有适配器在相同alpha值下的外观

衰减:

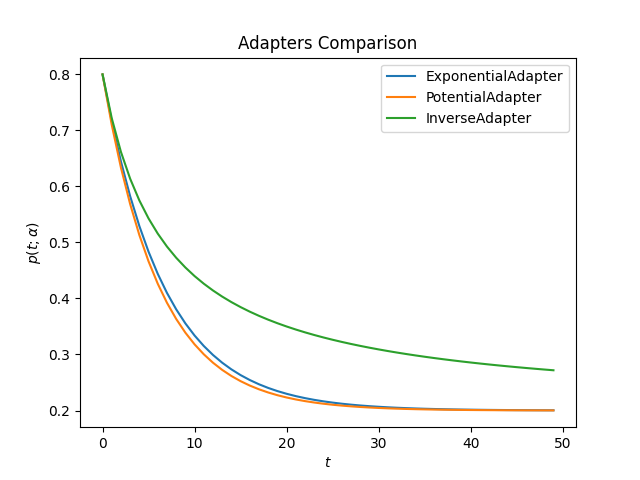
升序：

import matplotlib.pyplot as plt
from sklearn_genetic.schedules import ExponentialAdapter, PotentialAdapter, InverseAdapter


params = {"initial_value": 0.2, "end_value": 0.8, "adaptive_rate": 0.15}  # Ascend
adapters = [ExponentialAdapter(**params), PotentialAdapter(**params), InverseAdapter(**params)]

for adapter in adapters:
    adapter_result = [adapter.step() for _ in range(50)]

    plt.plot(adapter_result, label=f"{type(adapter).__name__}")

plt.xlabel(r'$t$')
plt.ylabel(r'$p(t; \alpha)$')
plt.title("Adapters Comparison")
plt.legend()
plt.show()

完整示例

在本示例中，我们希望为变异概率创建一个衰减策略，并为交叉概率创建一个递增策略，分别称之为\(p_{mt}(t; \alpha)\)和\(p_{cr}(t; \alpha)\)；这将使优化器在初始迭代中探索更多样化的解决方案。需要注意的是，在此场景下，我们必须谨慎选择\(\alpha, p_0, p_f\)，这是因为进化实现要求：

\[p_{mt}(t; \alpha) + p_{cr}(t; \alpha) <= 1; \forall t\]

同样的思路可以应用于超参数调优或特征选择。

from sklearn_genetic import GASearchCV
from sklearn_genetic import ExponentialAdapter
from sklearn_genetic.space import Continuous, Categorical, Integer
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split, StratifiedKFold
from sklearn.datasets import load_digits
from sklearn.metrics import accuracy_score

data = load_digits()
n_samples = len(data.images)
X = data.images.reshape((n_samples, -1))
y = data['target']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)

clf = RandomForestClassifier()

mutation_adapter = ExponentialAdapter(initial_value=0.8, end_value=0.2, adaptive_rate=0.1)
crossover_adapter = ExponentialAdapter(initial_value=0.2, end_value=0.8, adaptive_rate=0.1)

param_grid = {'min_weight_fraction_leaf': Continuous(0.01, 0.5, distribution='log-uniform'),
              'bootstrap': Categorical([True, False]),
              'max_depth': Integer(2, 30),
              'max_leaf_nodes': Integer(2, 35),
              'n_estimators': Integer(100, 300)}

cv = StratifiedKFold(n_splits=3, shuffle=True)

evolved_estimator = GASearchCV(estimator=clf,
                               cv=cv,
                               scoring='accuracy',
                               population_size=20,
                               generations=25,
                               mutation_probability=mutation_adapter,
                               crossover_probability=crossover_adapter,
                               param_grid=param_grid,
                               n_jobs=-1)

# Train and optimize the estimator
evolved_estimator.fit(X_train, y_train)
# Best parameters found
print(evolved_estimator.best_params_)
# Use the model fitted with the best parameters
y_predict_ga = evolved_estimator.predict(X_test)
print(accuracy_score(y_test, y_predict_ga))

# Saved metadata for further analysis
print("Stats achieved in each generation: ", evolved_estimator.history)
print("Best k solutions: ", evolved_estimator.hof)