理解评估流程

本文将解释超参数调优中的评估流程工作原理，以及如何使用不同的验证策略。

参数

GASearchCV 类需要一个名为 cv 的参数。 这代表交叉验证，它接受任何 scikit-learn 的策略， 例如 K折、重复K折、分层K折等。 您可以在scikit-learn文档中找到更多相关信息。

另一个相关参数是scoring，这是模型用来决定哪个模型更好的评估指标， 例如对于分类问题可以是准确率、精确率、召回率， 对于回归问题可以是r2、max_error、neg_root_mean_squared_error。 要查看完整的指标列表，请点击这里

进化算法背景

遗传算法(GA)是一种受自然选择启发的元启发式过程，通常用于优化和搜索问题，其基础是一组函数如变异、交叉和选择，我们称这些为遗传算子。 在本节中，我将交替使用以下术语以建立遗传算法与机器学习之间的联系：

超参数的一个选择→个体， 种群→多个个体， 世代→包含固定种群的单次迭代， 适应度值→交叉验证分数。

虽然存在多种变体，但通常需要遵循的步骤如下：

  1. 随机生成一个初始种群（包含多组不同的超参数组合）；这被称为第0代。

  2. 评估种群中每个个体的适应度值，在机器学习中，即获取交叉验证分数。

  3. 通过使用多种遗传算子生成新一代。 重复步骤2和3，直到满足停止条件。

让我们一步步来。

创建第0代并进行评估：

如前所述，您可以生成一组随机的超参数，也可以手动添加一些您已经尝试过并认为是不错候选的参数。

每组通常以染色体形式编码，即该组的二进制表示， 例如，如果我们设置第一代的大小为3个个体，它将看起来像这样：

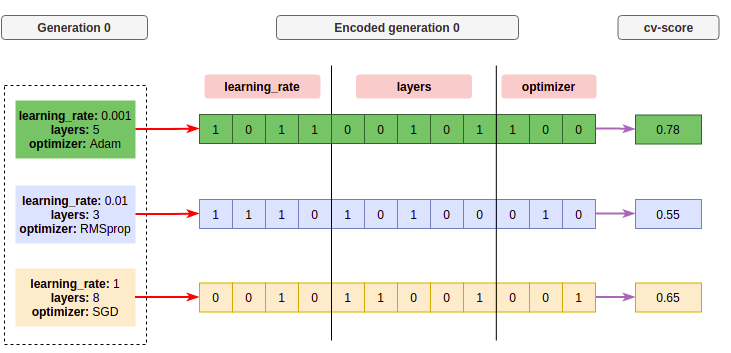
../_images/understandcv_generation0.png

在这一代中，我们获得三个被映射为染色体（二进制）表示的个体， 使用红色箭头表示的编码函数，染色体中的每个方框都是一个基因。 染色体的固定部分是超参数之一。 然后我们使用评分函数获得每个候选者的交叉验证分数（适应度）， 如紫色箭头所示。

创建新一代：

现在我们可以创建一组新的候选方案，如前所述，存在多种遗传算子，我将展示其中最常用的几种：

交叉操作：

该算子通过选取两条父代染色体并进行交配以产生新的子代，选择父代的方式可以采用概率分布函数，该函数会给予适应度更高的个体更大的选择概率。假设个体1和3被选中，那么我们可以在每个父代上随机选取两个点进行交叉操作，如下所示：

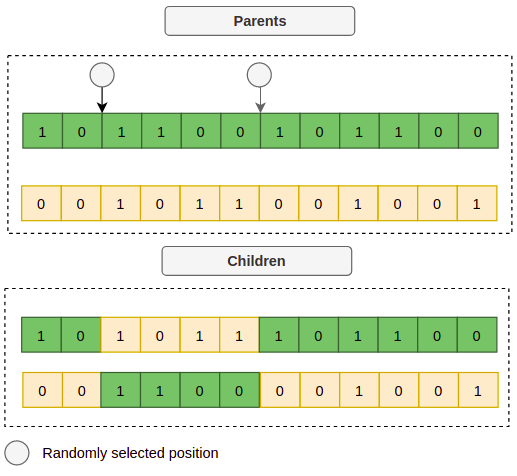
../_images/understandcv_crossover.png

现在这些子代代表了一组新的超参数，如果我们解码每个子代，可能会得到例如：

Child 1: {"learning_rate": 0.015, "layers": 4, "optimizer": "Adam"}
Child 2: {"learning_rate": 0.4, "layers": 6, "optimizer": "SGD"}

但在相同的超参数集上进行交叉操作，经过多次迭代后可能会产生相似的结果， 因此我们会陷入相同类型的解决方案中，这就是为什么我们引入了变异等其他操作。

变异：

该操作符允许以足够低的概率（< ~0.1）随机改变一个基因或整个超参数，从而创建更多样化的集合。 以前图中的子代1为例，我们随机选取一个基因并改变其值：

../_images/understandcv_mutantchild.png

或者甚至可以改变整个参数，例如优化器：

../_images/understandcv_mutantparameter.png

精英保留机制：

该选择策略指的是在每一代中筛选最优个体的过程，以确保其信息能在代际间传递。这种方法非常直观——只需根据适应度值选取前k个最优个体，并将其复制到下一代。在执行这些操作后，新一代的种群可能呈现如下形态：

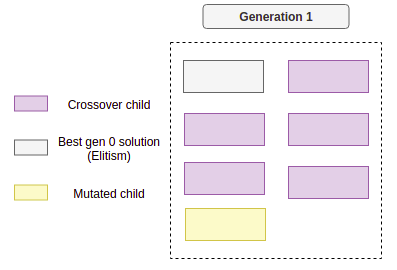
../_images/understandcv_generation1.png

从现在开始，只需重复这个过程若干代，直到满足停止条件， 这些条件可以是例如：

  • 已达到最大世代数。

  • 进程运行时间已超出预算时间。

  • 过去n代没有出现超过阈值的性能提升。

步骤

现在，转到这个包的实现部分。 GASearchCV评估候选方案的方式如下：

  • 首先根据param_grid定义随机选择多组超参数，总组数由population_size参数决定。

  • 它会为每组超参数拟合一个模型，并根据cv和scoring设置计算交叉验证分数。

  • 在评估每个候选方案后，系统会计算适应度(fitness)、适应度标准差(fitness_std)、最大适应度(fitness_max)和最小适应度(fitness_min)，如果verbose=True，这些指标会被记录到控制台。适应度是指所选评估指标的代称，但这里计算的是当前代所有候选方案的平均值，这意味着如果有10组不同的超参数组合，适应度值就是这10个评估候选方案的平均得分，其他指标的计算方式也相同。

  • 现在它会创建新的超参数集合（代际），这些集合是通过将上一代与不同策略相结合而产生的，这些策略取决于所选的algorithms。

  • 它会重复步骤2、3和4，直到达到设定的世代数，或者回调函数终止该过程。

  • 最终，算法会选择表现最佳的个体交叉验证分数对应的超参数组合作为最优解。

这些步骤可以这样表示，每一行代表几种可能的自然过程之一，如交配、交叉、选择和变异：

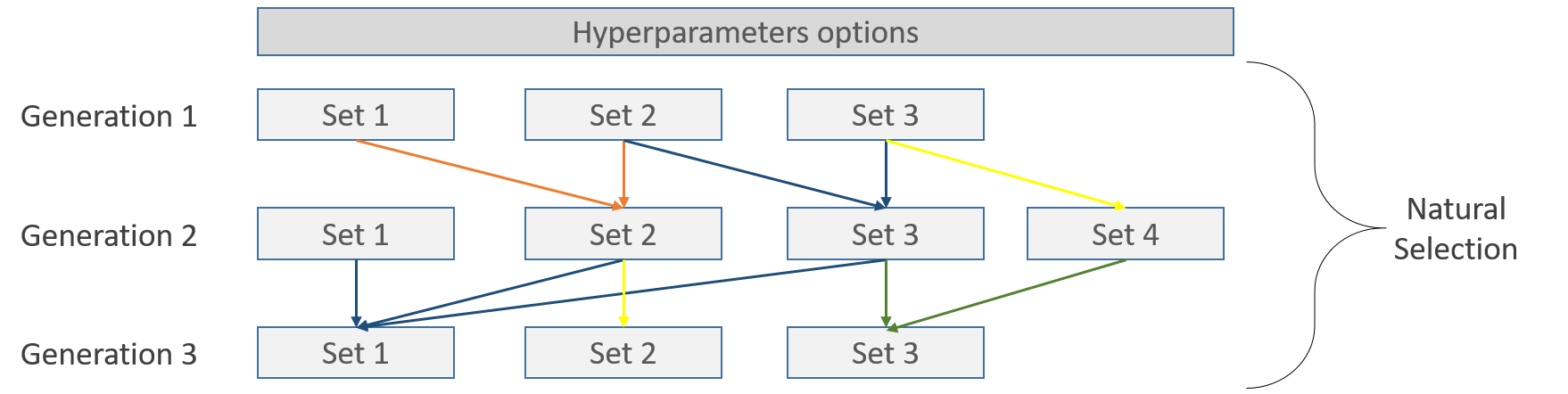
../_images/genetic_cv.png

在每个集合内部进行交叉验证，例如采用5折策略

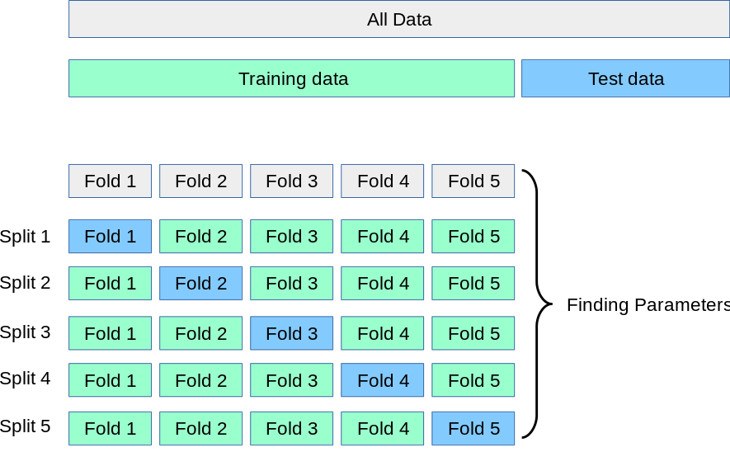
../_images/k-folds.png

图片取自 scikit-learn

示例

本示例将使用波士顿房价数据集中的回归问题。 我们将采用5折交叉验证，并以r-squared指标作为评估标准。

最后，我们将打印出前4个解决方案以及在测试集上最佳超参数组合对应的r-squared值。

from sklearn_genetic import GASearchCV
from sklearn_genetic.space import Integer, Categorical, Continuous
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split, KFold
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import r2_score
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

data = load_diabetes()

y = data["target"]
X = data["data"]

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.33, random_state=42)

cv = KFold(n_splits=5, shuffle=True)

clf = DecisionTreeRegressor()

pipe = Pipeline([('scaler', StandardScaler()), ('clf', clf)])

param_grid = {
    "clf__ccp_alpha": Continuous(0, 1),
    "clf__criterion": Categorical(["squared_error", "absolute_error"]),
    "clf__max_depth": Integer(2, 20),
    "clf__min_samples_split": Integer(2, 30),
}

evolved_estimator = GASearchCV(
    estimator=pipe,
    cv=3,
    scoring="r2",
    population_size=15,
    generations=20,
    tournament_size=3,
    elitism=True,
    keep_top_k=4,
    crossover_probability=0.9,
    mutation_probability=0.05,
    param_grid=param_grid,
    criteria="max",
    algorithm="eaMuCommaLambda",
    n_jobs=-1,
)

evolved_estimator.fit(X_train, y_train)
y_predict_ga = evolved_estimator.predict(X_test)
r_squared = r2_score(y_test, y_predict_ga)

print(evolved_estimator.best_params_)
print("r-squared: ", "{:.2f}".format(r_squared))