指数平滑

让我们考虑Hyndman和Athanasopoulos[1]关于指数平滑的优秀著作中的第7章。我们将逐一完成本章中的所有示例。

[1] Hyndman, Rob J., 和 George Athanasopoulos. 预测：原理与实践. OTexts, 2014.

加载数据

首先我们加载一些数据。为了方便起见，我们在笔记本中包含了R数据。

[1]:

import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.api import ExponentialSmoothing, SimpleExpSmoothing, Holt

%matplotlib inline

data = [
    446.6565,
    454.4733,
    455.663,
    423.6322,
    456.2713,
    440.5881,
    425.3325,
    485.1494,
    506.0482,
    526.792,
    514.2689,
    494.211,
]
index = pd.date_range(start="1996", end="2008", freq="Y")
oildata = pd.Series(data, index)

data = [
    17.5534,
    21.86,
    23.8866,
    26.9293,
    26.8885,
    28.8314,
    30.0751,
    30.9535,
    30.1857,
    31.5797,
    32.5776,
    33.4774,
    39.0216,
    41.3864,
    41.5966,
]
index = pd.date_range(start="1990", end="2005", freq="Y")
air = pd.Series(data, index)

data = [
    263.9177,
    268.3072,
    260.6626,
    266.6394,
    277.5158,
    283.834,
    290.309,
    292.4742,
    300.8307,
    309.2867,
    318.3311,
    329.3724,
    338.884,
    339.2441,
    328.6006,
    314.2554,
    314.4597,
    321.4138,
    329.7893,
    346.3852,
    352.2979,
    348.3705,
    417.5629,
    417.1236,
    417.7495,
    412.2339,
    411.9468,
    394.6971,
    401.4993,
    408.2705,
    414.2428,
]
index = pd.date_range(start="1970", end="2001", freq="Y")
livestock2 = pd.Series(data, index)

data = [407.9979, 403.4608, 413.8249, 428.105, 445.3387, 452.9942, 455.7402]
index = pd.date_range(start="2001", end="2008", freq="Y")
livestock3 = pd.Series(data, index)

data = [
    41.7275,
    24.0418,
    32.3281,
    37.3287,
    46.2132,
    29.3463,
    36.4829,
    42.9777,
    48.9015,
    31.1802,
    37.7179,
    40.4202,
    51.2069,
    31.8872,
    40.9783,
    43.7725,
    55.5586,
    33.8509,
    42.0764,
    45.6423,
    59.7668,
    35.1919,
    44.3197,
    47.9137,
]
index = pd.date_range(start="2005", end="2010-Q4", freq="QS-OCT")
aust = pd.Series(data, index)

/var/folders/xc/cwj7_pwj6lb0lkpyjtcbm7y80000gn/T/ipykernel_80852/536270367.py:23: FutureWarning: 'Y' is deprecated and will be removed in a future version, please use 'YE' instead.
  index = pd.date_range(start="1996", end="2008", freq="Y")
/var/folders/xc/cwj7_pwj6lb0lkpyjtcbm7y80000gn/T/ipykernel_80852/536270367.py:43: FutureWarning: 'Y' is deprecated and will be removed in a future version, please use 'YE' instead.
  index = pd.date_range(start="1990", end="2005", freq="Y")
/var/folders/xc/cwj7_pwj6lb0lkpyjtcbm7y80000gn/T/ipykernel_80852/536270367.py:79: FutureWarning: 'Y' is deprecated and will be removed in a future version, please use 'YE' instead.
  index = pd.date_range(start="1970", end="2001", freq="Y")
/var/folders/xc/cwj7_pwj6lb0lkpyjtcbm7y80000gn/T/ipykernel_80852/536270367.py:83: FutureWarning: 'Y' is deprecated and will be removed in a future version, please use 'YE' instead.
  index = pd.date_range(start="2001", end="2008", freq="Y")

简单指数平滑

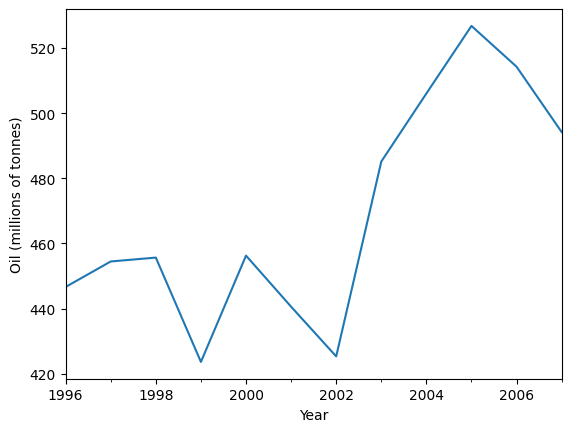
让我们使用简单指数平滑法来预测下面的石油数据。

[2]:

ax = oildata.plot()
ax.set_xlabel("Year")
ax.set_ylabel("Oil (millions of tonnes)")
print("Figure 7.1: Oil production in Saudi Arabia from 1996 to 2007.")

Figure 7.1: Oil production in Saudi Arabia from 1996 to 2007.
../../../_images/examples_notebooks_generated_exponential_smoothing_4_1.png

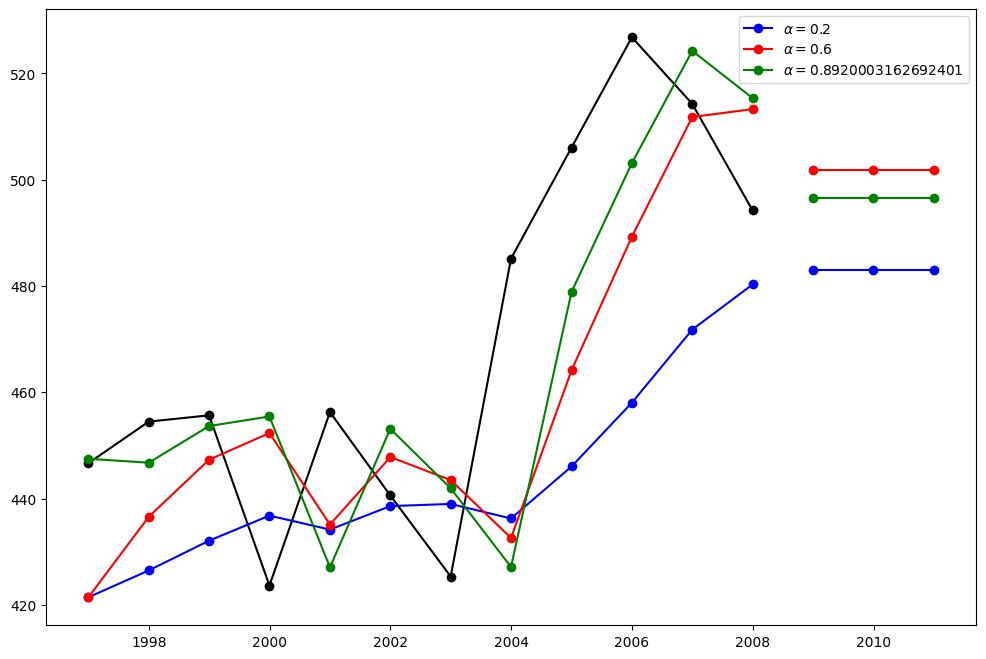
这里我们运行了三种简单指数平滑的变体：1. 在 fit1 中，我们不使用自动优化，而是选择显式地为模型提供 \(\alpha=0.2\) 参数 2. 在 fit2 中，如上所述，我们选择 \(\alpha=0.6\) 3. 在 fit3 中，我们允许 statsmodels 自动为我们找到优化的 \(\alpha\) 值。这是推荐的方法。

[3]:

fit1 = SimpleExpSmoothing(oildata, initialization_method="heuristic").fit(
    smoothing_level=0.2, optimized=False
)
fcast1 = fit1.forecast(3).rename(r"$\alpha=0.2$")
fit2 = SimpleExpSmoothing(oildata, initialization_method="heuristic").fit(
    smoothing_level=0.6, optimized=False
)
fcast2 = fit2.forecast(3).rename(r"$\alpha=0.6$")
fit3 = SimpleExpSmoothing(oildata, initialization_method="estimated").fit()
fcast3 = fit3.forecast(3).rename(r"$\alpha=%s$" % fit3.model.params["smoothing_level"])

plt.figure(figsize=(12, 8))
plt.plot(oildata, marker="o", color="black")
plt.plot(fit1.fittedvalues, marker="o", color="blue")
(line1,) = plt.plot(fcast1, marker="o", color="blue")
plt.plot(fit2.fittedvalues, marker="o", color="red")
(line2,) = plt.plot(fcast2, marker="o", color="red")
plt.plot(fit3.fittedvalues, marker="o", color="green")
(line3,) = plt.plot(fcast3, marker="o", color="green")
plt.legend([line1, line2, line3], [fcast1.name, fcast2.name, fcast3.name])

[3]:

<matplotlib.legend.Legend at 0x10dc27ed0>
../../../_images/examples_notebooks_generated_exponential_smoothing_6_1.png

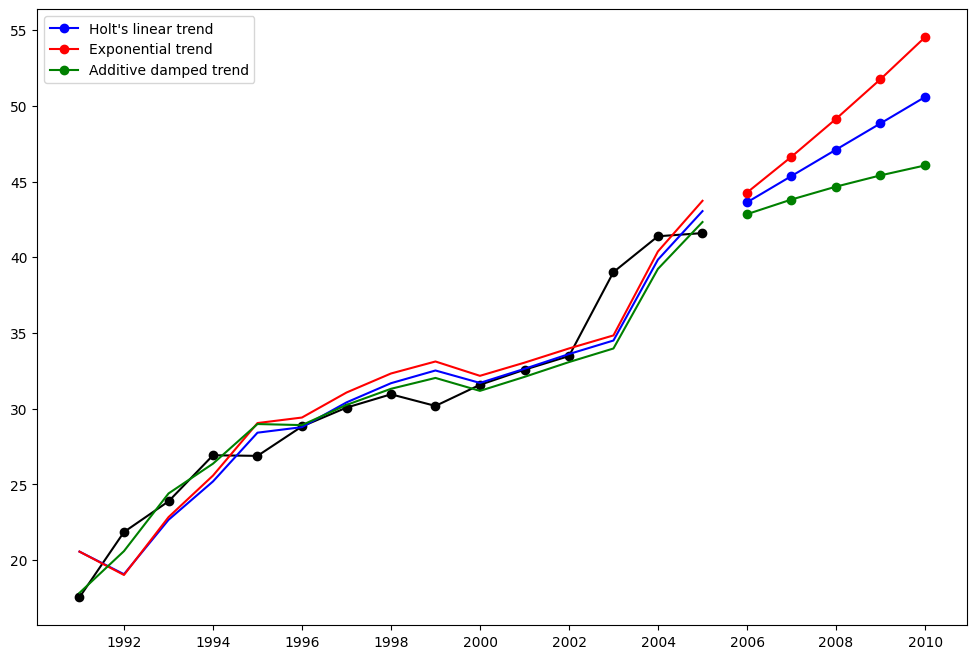
霍尔特方法

让我们来看另一个例子。这次我们使用空气污染数据和Holt方法。我们将再次拟合三个例子。1. 在fit1中，我们再次选择不使用优化器，并为\(\alpha=0.8\)和\(\beta=0.2\)提供显式值。2. 在fit2中，我们做了与fit1相同的事情，但选择使用指数模型而不是Holt的加法模型。3. 在fit3中，我们使用了Holt加法模型的阻尼版本，但允许阻尼参数\(\phi\)进行优化，同时固定\(\alpha=0.8\)和\(\beta=0.2\)的值。

[4]:

fit1 = Holt(air, initialization_method="estimated").fit(
    smoothing_level=0.8, smoothing_trend=0.2, optimized=False
)
fcast1 = fit1.forecast(5).rename("Holt's linear trend")
fit2 = Holt(air, exponential=True, initialization_method="estimated").fit(
    smoothing_level=0.8, smoothing_trend=0.2, optimized=False
)
fcast2 = fit2.forecast(5).rename("Exponential trend")
fit3 = Holt(air, damped_trend=True, initialization_method="estimated").fit(
    smoothing_level=0.8, smoothing_trend=0.2
)
fcast3 = fit3.forecast(5).rename("Additive damped trend")

plt.figure(figsize=(12, 8))
plt.plot(air, marker="o", color="black")
plt.plot(fit1.fittedvalues, color="blue")
(line1,) = plt.plot(fcast1, marker="o", color="blue")
plt.plot(fit2.fittedvalues, color="red")
(line2,) = plt.plot(fcast2, marker="o", color="red")
plt.plot(fit3.fittedvalues, color="green")
(line3,) = plt.plot(fcast3, marker="o", color="green")
plt.legend([line1, line2, line3], [fcast1.name, fcast2.name, fcast3.name])

[4]:

<matplotlib.legend.Legend at 0x10dcd81d0>
../../../_images/examples_notebooks_generated_exponential_smoothing_8_1.png

季节性调整数据

让我们来看一些季节性调整后的牲畜数据。我们拟合了五个Holt模型。下表允许我们在使用指数与加法以及阻尼与非阻尼时比较结果。

注意：fit4 不允许通过提供固定值 \(\phi=0.98\) 来优化参数 \(\phi\)

[5]:

fit1 = SimpleExpSmoothing(livestock2, initialization_method="estimated").fit()
fit2 = Holt(livestock2, initialization_method="estimated").fit()
fit3 = Holt(livestock2, exponential=True, initialization_method="estimated").fit()
fit4 = Holt(livestock2, damped_trend=True, initialization_method="estimated").fit(
    damping_trend=0.98
)
fit5 = Holt(
    livestock2, exponential=True, damped_trend=True, initialization_method="estimated"
).fit()
params = [
    "smoothing_level",
    "smoothing_trend",
    "damping_trend",
    "initial_level",
    "initial_trend",
]
results = pd.DataFrame(
    index=[r"$\alpha$", r"$\beta$", r"$\phi$", r"$l_0$", "$b_0$", "SSE"],
    columns=["SES", "Holt's", "Exponential", "Additive", "Multiplicative"],
)
results["SES"] = [fit1.params[p] for p in params] + [fit1.sse]
results["Holt's"] = [fit2.params[p] for p in params] + [fit2.sse]
results["Exponential"] = [fit3.params[p] for p in params] + [fit3.sse]
results["Additive"] = [fit4.params[p] for p in params] + [fit4.sse]
results["Multiplicative"] = [fit5.params[p] for p in params] + [fit5.sse]
results

[5]:
SES Holt's Exponential Additive Multiplicative
$\alpha$ 1.000000 0.974306 9.776418e-01 0.978850 0.974894
$\beta$ NaN 0.000000 3.628848e-07 0.000000 0.000026
$\phi$ NaN NaN NaN 0.980000 0.981636
$l_0$ 263.917735 258.882592 2.603437e+02 257.357619 258.950949
$b_0$ NaN 5.010781 1.013780e+00 6.644640 1.038157
SSE 6761.350235 6004.138200 6.104197e+03 6036.555004 6082.163796

季节性调整数据的图表

以下图表允许我们评估上述表格拟合的水平和斜率/趋势分量。

[6]:

for fit in [fit2, fit4]:
    pd.DataFrame(np.c_[fit.level, fit.trend]).rename(
        columns={0: "level", 1: "slope"}
    ).plot(subplots=True)
plt.show()
print(
    "Figure 7.4: Level and slope components for Holt’s linear trend method and the additive damped trend method."
)
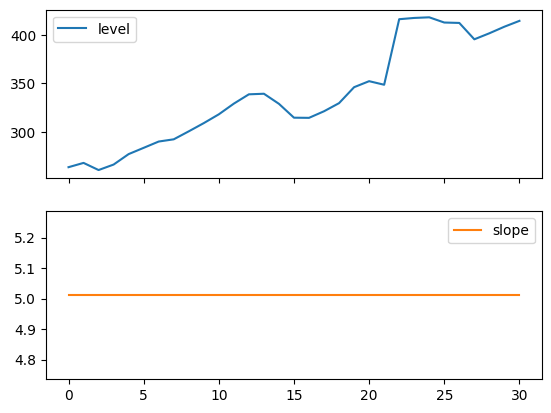
../../../_images/examples_notebooks_generated_exponential_smoothing_12_0.png
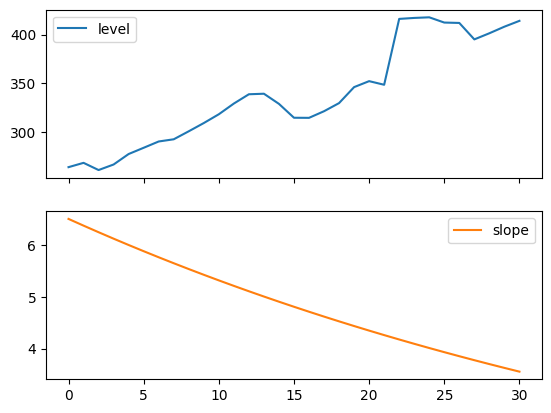
../../../_images/examples_notebooks_generated_exponential_smoothing_12_1.png 
Figure 7.4: Level and slope components for Holt’s linear trend method and the additive damped trend method.

比较

这里我们绘制了简单指数平滑法和霍尔特方法在各种加法、指数和阻尼组合下的比较。所有模型的参数将由statsmodels优化。

[7]:

fit1 = SimpleExpSmoothing(livestock2, initialization_method="estimated").fit()
fcast1 = fit1.forecast(9).rename("SES")
fit2 = Holt(livestock2, initialization_method="estimated").fit()
fcast2 = fit2.forecast(9).rename("Holt's")
fit3 = Holt(livestock2, exponential=True, initialization_method="estimated").fit()
fcast3 = fit3.forecast(9).rename("Exponential")
fit4 = Holt(livestock2, damped_trend=True, initialization_method="estimated").fit(
    damping_trend=0.98
)
fcast4 = fit4.forecast(9).rename("Additive Damped")
fit5 = Holt(
    livestock2, exponential=True, damped_trend=True, initialization_method="estimated"
).fit()
fcast5 = fit5.forecast(9).rename("Multiplicative Damped")

ax = livestock2.plot(color="black", marker="o", figsize=(12, 8))
livestock3.plot(ax=ax, color="black", marker="o", legend=False)
fcast1.plot(ax=ax, color="red", legend=True)
fcast2.plot(ax=ax, color="green", legend=True)
fcast3.plot(ax=ax, color="blue", legend=True)
fcast4.plot(ax=ax, color="cyan", legend=True)
fcast5.plot(ax=ax, color="magenta", legend=True)
ax.set_ylabel("Livestock, sheep in Asia (millions)")
plt.show()
print(
    "Figure 7.5: Forecasting livestock, sheep in Asia: comparing forecasting performance of non-seasonal methods."
)
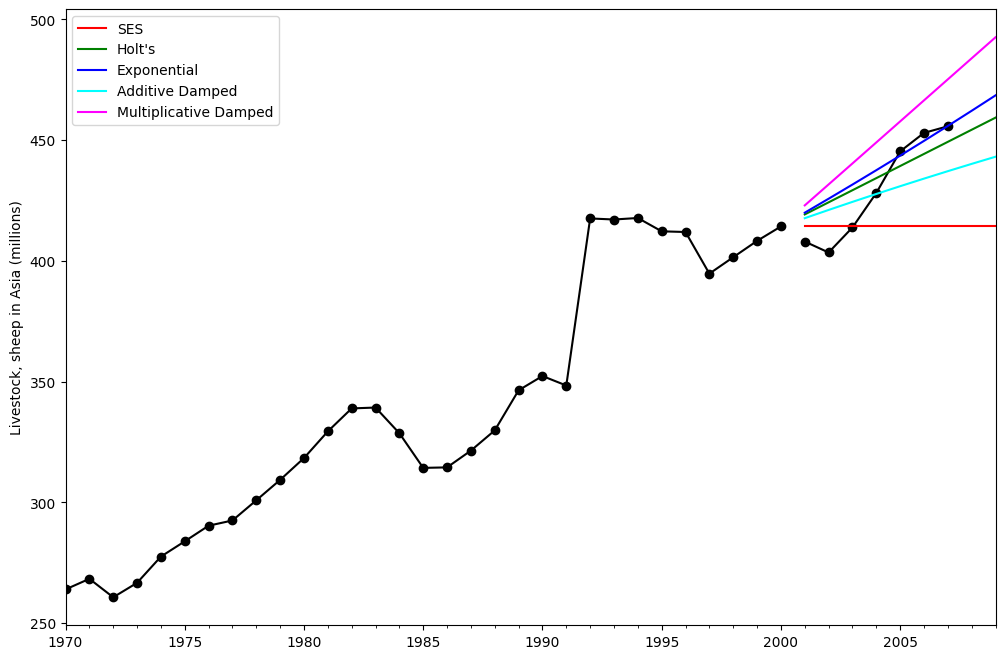
../../../_images/examples_notebooks_generated_exponential_smoothing_14_0.png 
Figure 7.5: Forecasting livestock, sheep in Asia: comparing forecasting performance of non-seasonal methods.

Holt’s Winters 季节性

最后，我们能够运行完整的Holt’s Winters季节性指数平滑，包括趋势分量和季节性分量。statsmodels允许所有组合，如下面的示例所示：1. fit1 加性趋势，周期为season_length=4的加性季节性，并使用Box-Cox变换。1. fit2 加性趋势，周期为season_length=4的乘性季节性，并使用Box-Cox变换。1. fit3 加性阻尼趋势，周期为season_length=4的加性季节性，并使用Box-Cox变换。1. fit4 加性阻尼趋势，周期为season_length=4的乘性季节性，并使用Box-Cox变换。

该图显示了fit1和fit2的结果和预测。该表允许我们比较结果和参数化。

[8]:

fit1 = ExponentialSmoothing(
    aust,
    seasonal_periods=4,
    trend="add",
    seasonal="add",
    use_boxcox=True,
    initialization_method="estimated",
).fit()
fit2 = ExponentialSmoothing(
    aust,
    seasonal_periods=4,
    trend="add",
    seasonal="mul",
    use_boxcox=True,
    initialization_method="estimated",
).fit()
fit3 = ExponentialSmoothing(
    aust,
    seasonal_periods=4,
    trend="add",
    seasonal="add",
    damped_trend=True,
    use_boxcox=True,
    initialization_method="estimated",
).fit()
fit4 = ExponentialSmoothing(
    aust,
    seasonal_periods=4,
    trend="add",
    seasonal="mul",
    damped_trend=True,
    use_boxcox=True,
    initialization_method="estimated",
).fit()
results = pd.DataFrame(
    index=[r"$\alpha$", r"$\beta$", r"$\phi$", r"$\gamma$", r"$l_0$", "$b_0$", "SSE"]
)
params = [
    "smoothing_level",
    "smoothing_trend",
    "damping_trend",
    "smoothing_seasonal",
    "initial_level",
    "initial_trend",
]
results["Additive"] = [fit1.params[p] for p in params] + [fit1.sse]
results["Multiplicative"] = [fit2.params[p] for p in params] + [fit2.sse]
results["Additive Dam"] = [fit3.params[p] for p in params] + [fit3.sse]
results["Multiplica Dam"] = [fit4.params[p] for p in params] + [fit4.sse]

ax = aust.plot(
    figsize=(10, 6),
    marker="o",
    color="black",
    title="Forecasts from Holt-Winters' multiplicative method",
)
ax.set_ylabel("International visitor night in Australia (millions)")
ax.set_xlabel("Year")
fit1.fittedvalues.plot(ax=ax, style="--", color="red")
fit2.fittedvalues.plot(ax=ax, style="--", color="green")

fit1.forecast(8).rename("Holt-Winters (add-add-seasonal)").plot(
    ax=ax, style="--", marker="o", color="red", legend=True
)
fit2.forecast(8).rename("Holt-Winters (add-mul-seasonal)").plot(
    ax=ax, style="--", marker="o", color="green", legend=True
)

plt.show()
print(
    "Figure 7.6: Forecasting international visitor nights in Australia using Holt-Winters method with both additive and multiplicative seasonality."
)

results
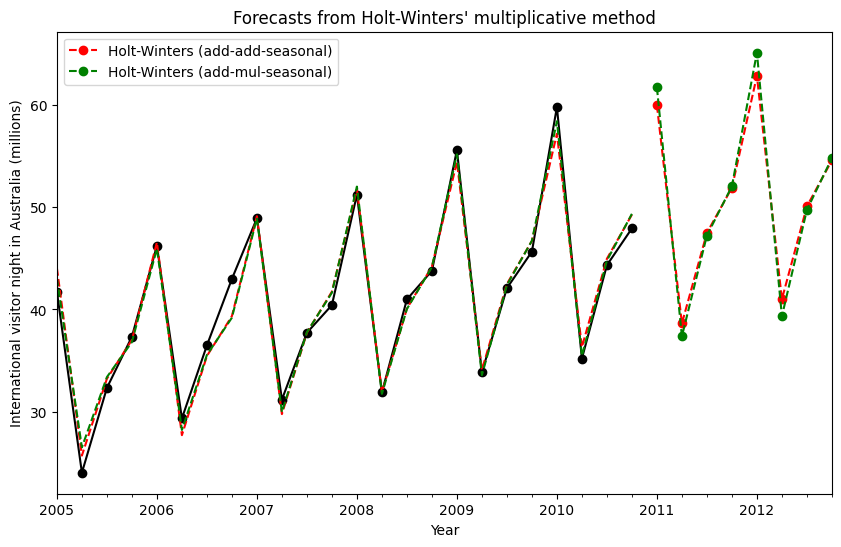
../../../_images/examples_notebooks_generated_exponential_smoothing_16_0.png 
Figure 7.6: Forecasting international visitor nights in Australia using Holt-Winters method with both additive and multiplicative seasonality.

[8]:
Additive Multiplicative Additive Dam Multiplica Dam
$\alpha$ 1.490116e-08 1.490116e-08 1.490116e-08 1.490116e-08
$\beta$ 1.409869e-08 1.308971e-23 6.490801e-09 5.042240e-09
$\phi$ NaN NaN 9.430416e-01 9.536044e-01
$\gamma$ 3.312830e-15 0.000000e+00 1.008101e-16 0.000000e+00
$l_0$ 1.119348e+01 1.106381e+01 1.084022e+01 9.899308e+00
$b_0$ 1.205396e-01 1.198963e-01 2.456750e-01 1.975449e-01
SSE 4.402746e+01 3.611262e+01 3.527620e+01 3.062033e+01

内部机制

可以获取指数平滑模型的内部信息。

这里我们展示了一些表格，允许您并排查看原始值 \(y_t\)、水平 \(l_t\)、趋势 \(b_t\)、季节 \(s_t\) 和拟合值 \(\hat{y}_t\)。请注意，如果未进行Box-Cox变换，这些值仅在原始数据的空间中具有有意义的值。

[9]:

fit1 = ExponentialSmoothing(
    aust,
    seasonal_periods=4,
    trend="add",
    seasonal="add",
    initialization_method="estimated",
).fit()
fit2 = ExponentialSmoothing(
    aust,
    seasonal_periods=4,
    trend="add",
    seasonal="mul",
    initialization_method="estimated",
).fit()

[10]:

df = pd.DataFrame(
    np.c_[aust, fit1.level, fit1.trend, fit1.season, fit1.fittedvalues],
    columns=[r"$y_t$", r"$l_t$", r"$b_t$", r"$s_t$", r"$\hat{y}_t$"],
    index=aust.index,
)
forecasts = fit1.forecast(8).rename(r"$\hat{y}_t$").to_frame()
df = pd.concat([df, forecasts], axis=0, sort=True)

[11]:

df = pd.DataFrame(
    np.c_[aust, fit2.level, fit2.trend, fit2.season, fit2.fittedvalues],
    columns=[r"$y_t$", r"$l_t$", r"$b_t$", r"$s_t$", r"$\hat{y}_t$"],
    index=aust.index,
)
forecasts = fit2.forecast(8).rename(r"$\hat{y}_t$").to_frame()
df = pd.concat([df, forecasts], axis=0, sort=True)

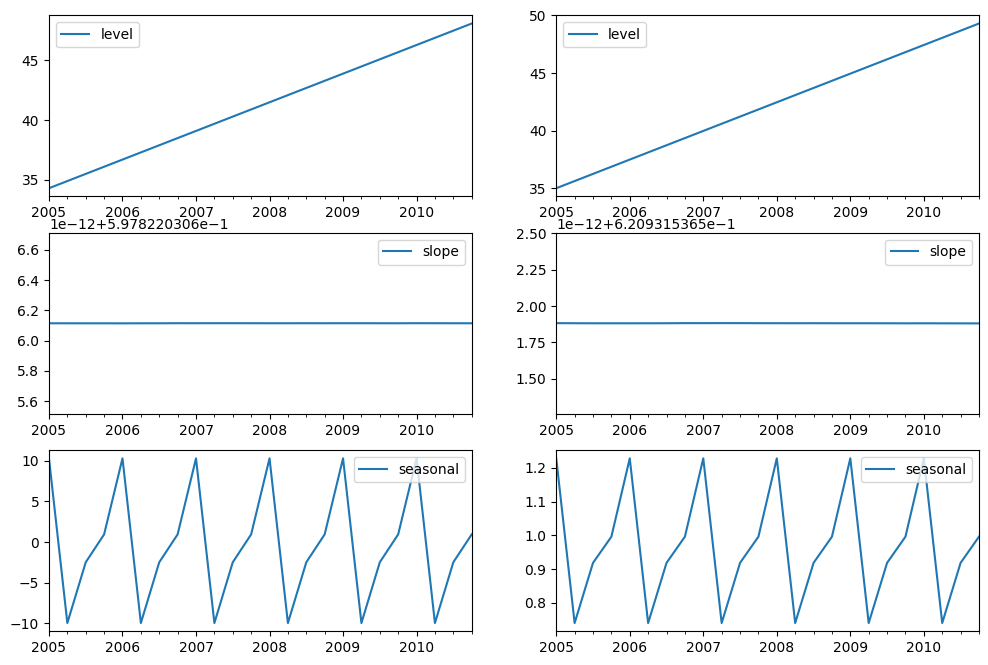
最后，让我们来看看模型的水平、斜率/趋势和季节性成分。

[12]:

states1 = pd.DataFrame(
    np.c_[fit1.level, fit1.trend, fit1.season],
    columns=["level", "slope", "seasonal"],
    index=aust.index,
)
states2 = pd.DataFrame(
    np.c_[fit2.level, fit2.trend, fit2.season],
    columns=["level", "slope", "seasonal"],
    index=aust.index,
)
fig, [[ax1, ax4], [ax2, ax5], [ax3, ax6]] = plt.subplots(3, 2, figsize=(12, 8))
states1[["level"]].plot(ax=ax1)
states1[["slope"]].plot(ax=ax2)
states1[["seasonal"]].plot(ax=ax3)
states2[["level"]].plot(ax=ax4)
states2[["slope"]].plot(ax=ax5)
states2[["seasonal"]].plot(ax=ax6)
plt.show()
../../../_images/examples_notebooks_generated_exponential_smoothing_22_0.png

模拟与置信区间

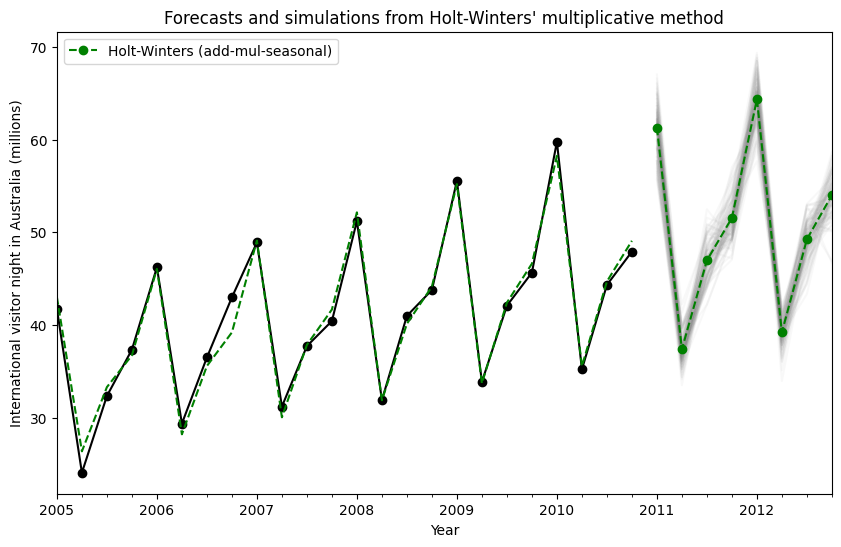
通过使用状态空间公式，我们可以进行未来值的模拟。数学细节在Hyndman和Athanasopoulos [2] 以及 HoltWintersResults.simulate 的文档中有描述。

类似于[2]中的示例，我们使用具有加性趋势、乘性季节性和乘性误差的模型。我们模拟未来最多8步，并进行1000次模拟。如下图所示，模拟结果与预测值非常吻合。

[2] Hyndman, Rob J., 和 George Athanasopoulos. 预测：原理与实践，第二版。OTexts, 2018.

[13]:

fit = ExponentialSmoothing(
    aust,
    seasonal_periods=4,
    trend="add",
    seasonal="mul",
    initialization_method="estimated",
).fit()
simulations = fit.simulate(8, repetitions=100, error="mul")

ax = aust.plot(
    figsize=(10, 6),
    marker="o",
    color="black",
    title="Forecasts and simulations from Holt-Winters' multiplicative method",
)
ax.set_ylabel("International visitor night in Australia (millions)")
ax.set_xlabel("Year")
fit.fittedvalues.plot(ax=ax, style="--", color="green")
simulations.plot(ax=ax, style="-", alpha=0.05, color="grey", legend=False)
fit.forecast(8).rename("Holt-Winters (add-mul-seasonal)").plot(
    ax=ax, style="--", marker="o", color="green", legend=True
)
plt.show()
../../../_images/examples_notebooks_generated_exponential_smoothing_24_0.png

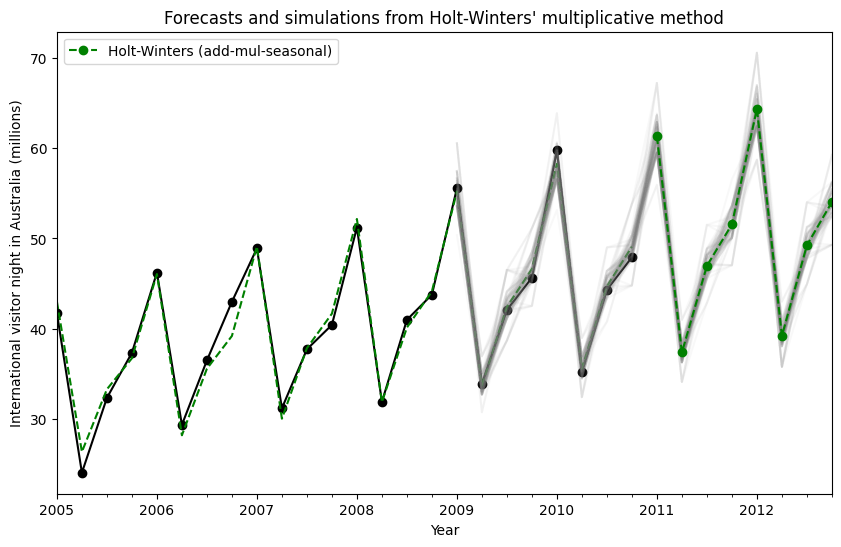
模拟也可以在不同的时间点开始，并且有多种选择来选择随机噪声。

[14]:

fit = ExponentialSmoothing(
    aust,
    seasonal_periods=4,
    trend="add",
    seasonal="mul",
    initialization_method="estimated",
).fit()
simulations = fit.simulate(
    16, anchor="2009-01-01", repetitions=100, error="mul", random_errors="bootstrap"
)

ax = aust.plot(
    figsize=(10, 6),
    marker="o",
    color="black",
    title="Forecasts and simulations from Holt-Winters' multiplicative method",
)
ax.set_ylabel("International visitor night in Australia (millions)")
ax.set_xlabel("Year")
fit.fittedvalues.plot(ax=ax, style="--", color="green")
simulations.plot(ax=ax, style="-", alpha=0.05, color="grey", legend=False)
fit.forecast(8).rename("Holt-Winters (add-mul-seasonal)").plot(
    ax=ax, style="--", marker="o", color="green", legend=True
)
plt.show()
../../../_images/examples_notebooks_generated_exponential_smoothing_26_0.png
Last update: Oct 16, 2024