时间序列过滤器¶
[1]:
%matplotlib inline
[2]:
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
[3]:
dta = sm.datasets.macrodata.load_pandas().data
[4]:
index = pd.Index(sm.tsa.datetools.dates_from_range("1959Q1", "2009Q3"))
print(index)
DatetimeIndex(['1959-03-31', '1959-06-30', '1959-09-30', '1959-12-31',
'1960-03-31', '1960-06-30', '1960-09-30', '1960-12-31',
'1961-03-31', '1961-06-30',
...
'2007-06-30', '2007-09-30', '2007-12-31', '2008-03-31',
'2008-06-30', '2008-09-30', '2008-12-31', '2009-03-31',
'2009-06-30', '2009-09-30'],
dtype='datetime64[ns]', length=203, freq=None)
[5]:
dta.index = index
del dta["year"]
del dta["quarter"]
[6]:
print(sm.datasets.macrodata.NOTE)
::
Number of Observations - 203
Number of Variables - 14
Variable name definitions::
year - 1959q1 - 2009q3
quarter - 1-4
realgdp - Real gross domestic product (Bil. of chained 2005 US$,
seasonally adjusted annual rate)
realcons - Real personal consumption expenditures (Bil. of chained
2005 US$, seasonally adjusted annual rate)
realinv - Real gross private domestic investment (Bil. of chained
2005 US$, seasonally adjusted annual rate)
realgovt - Real federal consumption expenditures & gross investment
(Bil. of chained 2005 US$, seasonally adjusted annual rate)
realdpi - Real private disposable income (Bil. of chained 2005
US$, seasonally adjusted annual rate)
cpi - End of the quarter consumer price index for all urban
consumers: all items (1982-84 = 100, seasonally adjusted).
m1 - End of the quarter M1 nominal money stock (Seasonally
adjusted)
tbilrate - Quarterly monthly average of the monthly 3-month
treasury bill: secondary market rate
unemp - Seasonally adjusted unemployment rate (%)
pop - End of the quarter total population: all ages incl. armed
forces over seas
infl - Inflation rate (ln(cpi_{t}/cpi_{t-1}) * 400)
realint - Real interest rate (tbilrate - infl)
[7]:
print(dta.head(10))
realgdp realcons realinv realgovt realdpi cpi m1 \
1959-03-31 2710.349 1707.4 286.898 470.045 1886.9 28.98 139.7
1959-06-30 2778.801 1733.7 310.859 481.301 1919.7 29.15 141.7
1959-09-30 2775.488 1751.8 289.226 491.260 1916.4 29.35 140.5
1959-12-31 2785.204 1753.7 299.356 484.052 1931.3 29.37 140.0
1960-03-31 2847.699 1770.5 331.722 462.199 1955.5 29.54 139.6
1960-06-30 2834.390 1792.9 298.152 460.400 1966.1 29.55 140.2
1960-09-30 2839.022 1785.8 296.375 474.676 1967.8 29.75 140.9
1960-12-31 2802.616 1788.2 259.764 476.434 1966.6 29.84 141.1
1961-03-31 2819.264 1787.7 266.405 475.854 1984.5 29.81 142.1
1961-06-30 2872.005 1814.3 286.246 480.328 2014.4 29.92 142.9
tbilrate unemp pop infl realint
1959-03-31 2.82 5.8 177.146 0.00 0.00
1959-06-30 3.08 5.1 177.830 2.34 0.74
1959-09-30 3.82 5.3 178.657 2.74 1.09
1959-12-31 4.33 5.6 179.386 0.27 4.06
1960-03-31 3.50 5.2 180.007 2.31 1.19
1960-06-30 2.68 5.2 180.671 0.14 2.55
1960-09-30 2.36 5.6 181.528 2.70 -0.34
1960-12-31 2.29 6.3 182.287 1.21 1.08
1961-03-31 2.37 6.8 182.992 -0.40 2.77
1961-06-30 2.29 7.0 183.691 1.47 0.81
[8]:
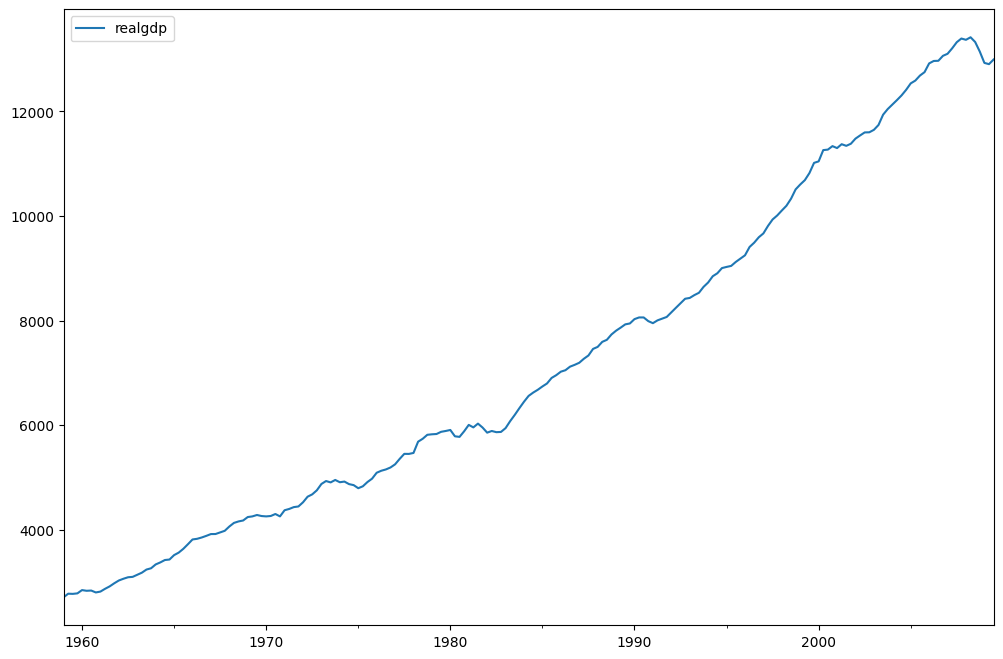
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111)
dta.realgdp.plot(ax=ax)
legend = ax.legend(loc="upper left")
legend.prop.set_size(20)
Hodrick-Prescott 滤波器¶
Hodrick-Prescott滤波器将时间序列\(y_t\)分解为趋势\(\tau_t\)和周期性成分\(\zeta_t\)
\[y_t = \tau_t + \zeta_t\]
通过最小化以下二次损失函数来确定组件
\[\begin{split}\min_{\\{ \tau_{t}\\} }\sum_{t}^{T}\zeta_{t}^{2}+\lambda\sum_{t=1}^{T}\left[\left(\tau_{t}-\tau_{t-1}\right)-\left(\tau_{t-1}-\tau_{t-2}\right)\right]^{2}\end{split}\]
[9]:
gdp_cycle, gdp_trend = sm.tsa.filters.hpfilter(dta.realgdp)
[10]:
gdp_decomp = dta[["realgdp"]].copy()
gdp_decomp["cycle"] = gdp_cycle
gdp_decomp["trend"] = gdp_trend
[11]:
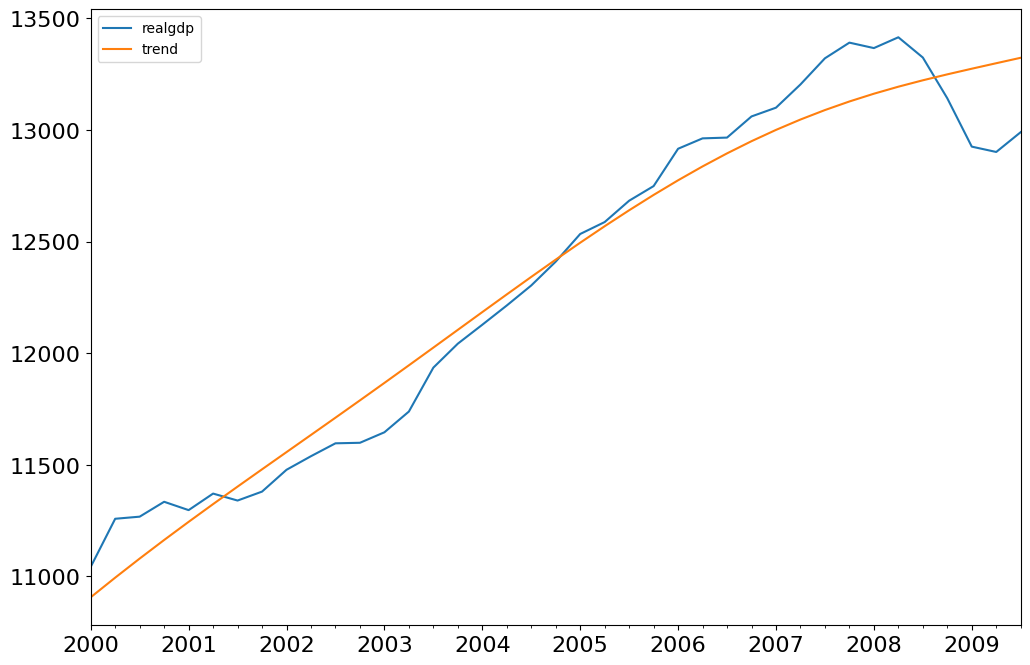
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111)
gdp_decomp[["realgdp", "trend"]]["2000-03-31":].plot(ax=ax, fontsize=16)
legend = ax.get_legend()
legend.prop.set_size(20)
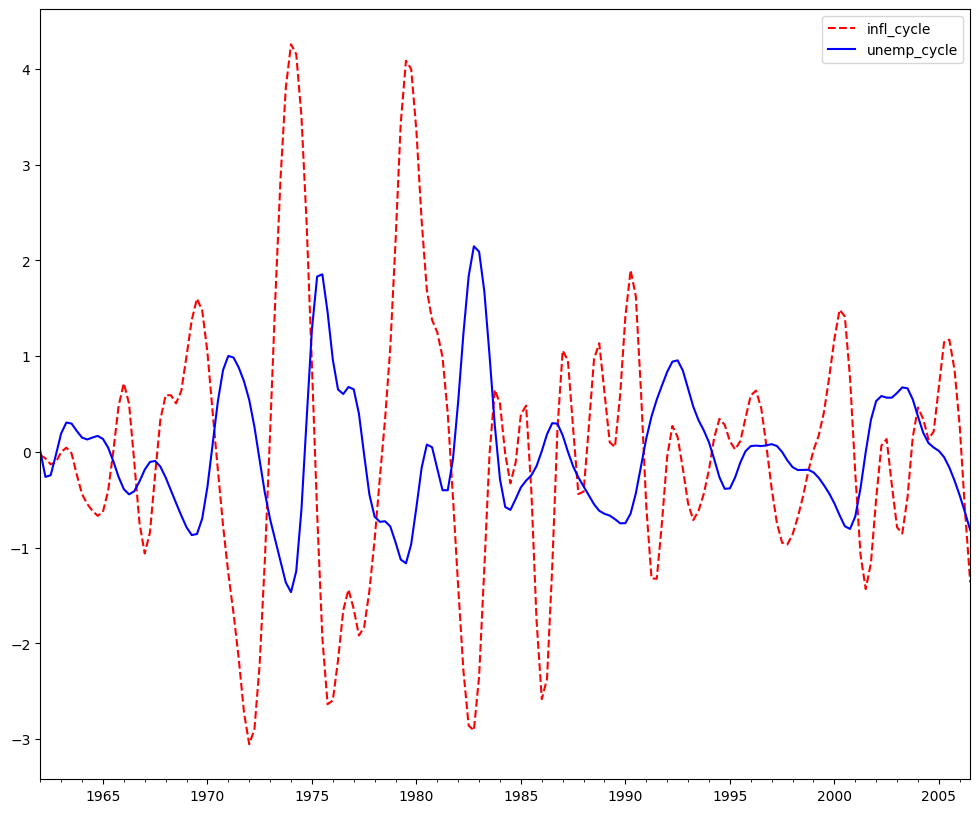
Baxter-King近似带通滤波器: 通货膨胀和失业¶
探讨通货膨胀和失业率呈反周期性的假设。¶
Baxter-King 滤波器旨在明确处理商业周期的周期性。通过将他们的带通滤波器应用于一个序列，他们生成一个不包含高于或低于商业周期波动的新序列。具体来说，BK 滤波器采用对称移动平均的形式
\[y_{t}^{*}=\sum_{k=-K}^{k=K}a_ky_{t-k}\]
其中 \(a_{-k}=a_k\) 且 \(\sum_{k=-k}^{K}a_k=0\) 以消除序列中的任何趋势，并使其平稳，如果序列是 I(1) 或 I(2)。
为了完整性，过滤器权重确定如下
\[a_{j} = B_{j}+\theta\text{ for }j=0,\pm1,\pm2,\dots,\pm K\]
\[B_{0} = \frac{\left(\omega_{2}-\omega_{1}\right)}{\pi}\]
\[B_{j} = \frac{1}{\pi j}\left(\sin\left(\omega_{2}j\right)-\sin\left(\omega_{1}j\right)\right)\text{ for }j=0,\pm1,\pm2,\dots,\pm K\]
其中 \(\theta\) 是一个归一化常数，使得权重之和为零。
\[\theta=\frac{-\sum_{j=-K^{K}b_{j}}}{2K+1}\]
\[\omega_{1}=\frac{2\pi}{P_{H}}\]
\[\omega_{2}=\frac{2\pi}{P_{L}}\]
\(P_L\) 和 \(P_H\) 是低和高截止频率的周期性。根据Burns和Mitchell关于美国商业周期的研究，建议周期持续时间为1.5到8年，我们默认使用 \(P_L=6\) 和 \(P_H=32\)。
[12]:
bk_cycles = sm.tsa.filters.bkfilter(dta[["infl", "unemp"]])
我们在两端丢失了K个观测值。建议对季度数据使用K=12。
[13]:
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(111)
bk_cycles.plot(ax=ax, style=["r--", "b-"])
[13]:
<Axes: >
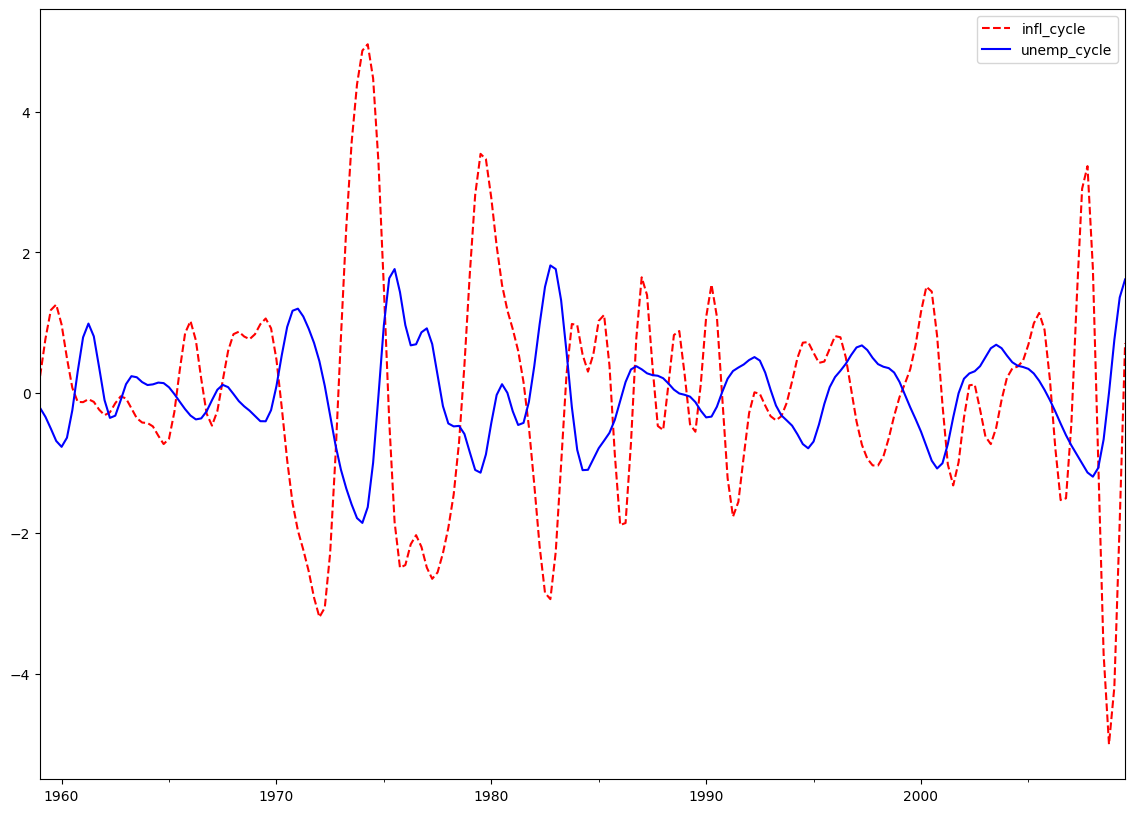
Christiano-Fitzgerald 近似带通滤波器: 通货膨胀和失业¶
Christiano-Fitzgerald 滤波器是 BK 的泛化，因此也可以被视为加权移动平均。然而，CF 滤波器在 \(t\) 处是不对称的，并且使用了整个序列。他们的滤波器的实现涉及在
\[y_{t}^{*}=B_{0}y_{t}+B_{1}y_{t+1}+\dots+B_{T-1-t}y_{T-1}+\tilde B_{T-t}y_{T}+B_{1}y_{t-1}+\dots+B_{t-2}y_{2}+\tilde B_{t-1}y_{1}\]
对于 \(t=3,4,...,T-2\)，其中
\[B_{j} = \frac{\sin(jb)-\sin(ja)}{\pi j},j\geq1\]
\[B_{0} = \frac{b-a}{\pi},a=\frac{2\pi}{P_{u}},b=\frac{2\pi}{P_{L}}\]
\(\tilde B_{T-t}\) 和 \(\tilde B_{t-1}\) 是 \(B_{j}\) 的线性函数，并且 \(t=1,2,T-1,\) 和 \(T\) 的值也是以类似的方式计算的。\(P_{U}\) 和 \(P_{L}\) 如上所述，具有相同的解释。
CF 滤波器适用于可能遵循随机游走的序列。
[14]:
print(sm.tsa.stattools.adfuller(dta["unemp"])[:3])
(np.float64(-2.5364584673346355), np.float64(0.10685366457233497), 9)
[15]:
print(sm.tsa.stattools.adfuller(dta["infl"])[:3])
(np.float64(-3.054514496257235), np.float64(0.030107620863486003), 2)
[16]:
cf_cycles, cf_trend = sm.tsa.filters.cffilter(dta[["infl", "unemp"]])
print(cf_cycles.head(10))
infl_cycle unemp_cycle
1959-03-31 0.237927 -0.216867
1959-06-30 0.770007 -0.343779
1959-09-30 1.177736 -0.511024
1959-12-31 1.256754 -0.686967
1960-03-31 0.972128 -0.770793
1960-06-30 0.491889 -0.640601
1960-09-30 0.070189 -0.249741
1960-12-31 -0.130432 0.301545
1961-03-31 -0.134155 0.788992
1961-06-30 -0.092073 0.985356
[17]:
fig = plt.figure(figsize=(14, 10))
ax = fig.add_subplot(111)
cf_cycles.plot(ax=ax, style=["r--", "b-"])
[17]:
<Axes: >
过滤假设先验存在商业周期。由于这一假设，许多宏观经济模型试图创建与脉冲响应函数形状相匹配的模型，而不是复制过滤序列的属性。请参阅VAR笔记本。
Last update:
Oct 16, 2024