理解图注意力网络

作者: Hao Zhang, Mufei Li, Minjie Wang Zheng Zhang

警告

The tutorial aims at gaining insights into the paper, with code as a mean of explanation. The implementation thus is NOT optimized for running efficiency. For recommended implementation, please refer to the official examples.

在本教程中，您将了解图注意力网络（GAT）以及如何在PyTorch中实现它。您还可以学习如何可视化并理解注意力机制所学到的内容。

论文中描述的研究图卷积网络（GCN）表明，结合局部图结构和节点级特征在节点分类任务上表现出色。然而，GCN的聚合方式是结构依赖的，这可能会影响其泛化能力。

一种解决方法是在所有邻居节点特征上简单平均，如研究论文GraphSAGE中所述。 然而，Graph Attention Network提出了一种不同类型的聚合方式。GAT使用特征依赖和无结构归一化的方式对邻居特征进行加权，采用注意力机制的风格。

将注意力引入GCN

GAT和GCN之间的关键区别在于如何聚合来自一跳邻域的信息。

对于GCN，图卷积操作生成邻居节点特征的归一化和。

\[h_i^{(l+1)}=\sigma\left(\sum_{j\in \mathcal{N}(i)} {\frac{1}{c_{ij}} W^{(l)}h^{(l)}_j}\right)\]

其中 \(\mathcal{N}(i)\) 是其一跳邻居的集合（要将 \(v_i\) 包含在集合中，只需为每个节点添加自环），\(c_{ij}=\sqrt{|\mathcal{N}(i)|}\sqrt{|\mathcal{N}(j)|}\) 是基于图结构的归一化常数，\(\sigma\) 是激活函数（GCN 使用 ReLU），\(W^{(l)}\) 是用于节点特征变换的共享权重矩阵。在 GraphSAGE 中提出的另一个模型采用了相同的更新规则，只是他们将 \(c_{ij}=|\mathcal{N}(i)|\)。

GAT 引入了注意力机制作为静态归一化卷积操作的替代。以下是计算第 \(l+1\) 层节点嵌入 \(h_i^{(l+1)}\) 的公式，该公式基于第 \(l\) 层的嵌入。

\[\begin{split}\begin{align} z_i^{(l)}&=W^{(l)}h_i^{(l)},&(1) \\ e_{ij}^{(l)}&=\text{LeakyReLU}(\vec a^{(l)^T}(z_i^{(l)}||z_j^{(l)})),&(2)\\ \alpha_{ij}^{(l)}&=\frac{\exp(e_{ij}^{(l)})}{\sum_{k\in \mathcal{N}(i)}^{}\exp(e_{ik}^{(l)})},&(3)\\ h_i^{(l+1)}&=\sigma\left(\sum_{j\in \mathcal{N}(i)} {\alpha^{(l)}_{ij} z^{(l)}_j }\right),&(4) \end{align}\end{split}\]

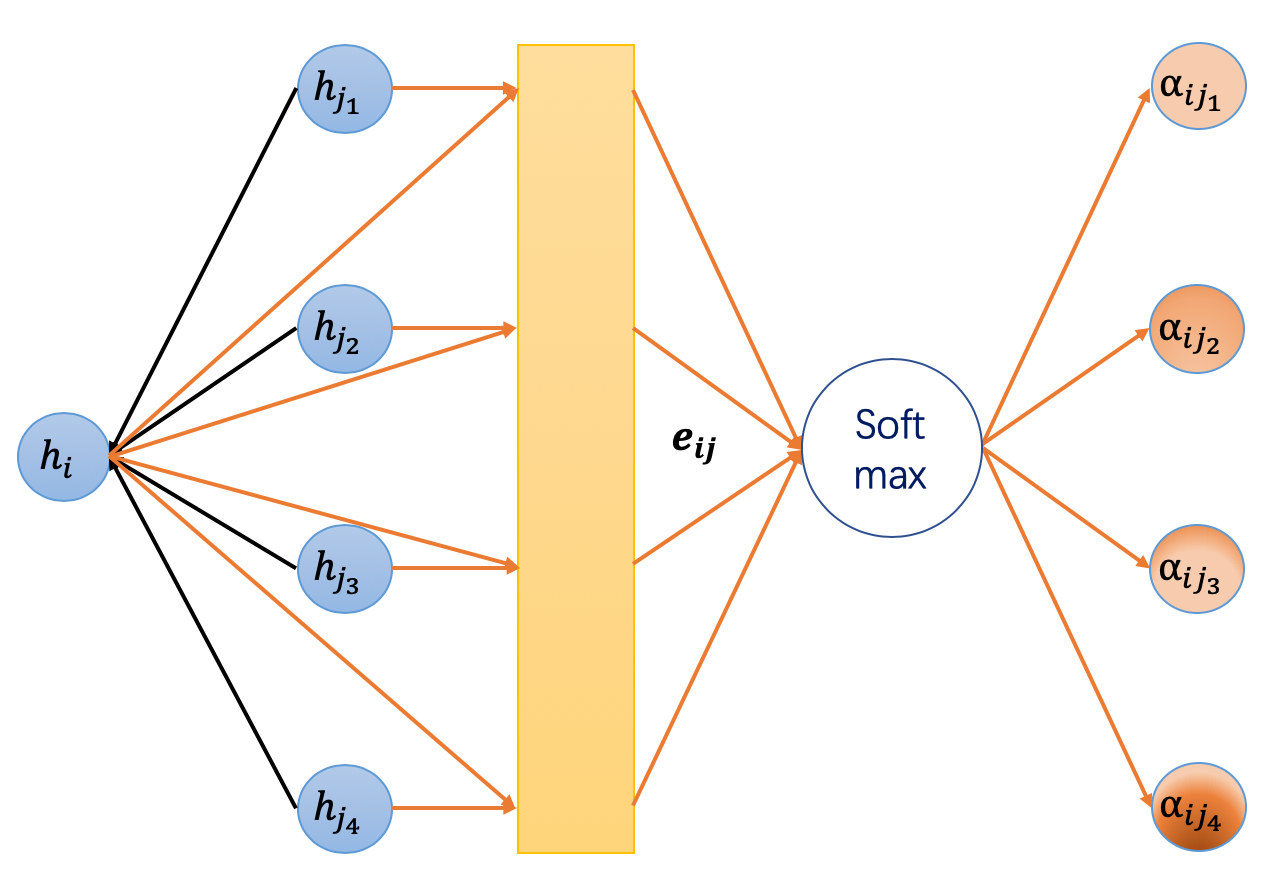
解释：

• 方程（1）是下层嵌入\(h_i^{(l)}\)的线性变换，\(W^{(l)}\)是其可学习的权重矩阵。

• 方程 (2) 计算了两个邻居之间的成对未归一化注意力分数。 这里，它首先连接两个节点的 \(z\) 嵌入，其中 \(||\) 表示连接，然后将其与可学习的权重向量 \(\vec a^{(l)}\) 进行点积，最后应用 LeakyReLU。这种形式的注意力通常称为 加法注意力，与 Transformer 模型中的点积注意力形成对比。

• 方程（3）应用了softmax来归一化每个节点传入边上的注意力分数。

• 方程（4）与GCN相似。来自邻居的嵌入被聚合在一起，通过注意力分数进行缩放。

论文中还有其他细节，例如 dropout 和跳跃连接。 为了简化起见，本教程中省略了这些细节。要查看更多细节， 请下载完整示例。 本质上，GAT 只是一个不同的聚合函数，它通过注意力机制对邻居的特征进行聚合，而不是简单的均值聚合。

DGL中的GAT

DGL 在 dgl.nn. 子包下提供了 GAT 层的现成实现。只需按如下方式导入 GATConv。

import os

os.environ["DGLBACKEND"] = "pytorch"

读者可以跳过以下逐步实现的解释，直接跳转到将所有内容整合在一起以查看训练和可视化结果。

首先，您可以对GATLayer模块在DGL中的实现有一个整体的印象。在本节中，将逐一分解上述四个公式。

注意

这是展示如何从头实现一个GAT。DGL提供了一个更高效的builtin GAT layer module。

import torch
import torch.nn as nn
import torch.nn.functional as F
from dgl.nn.pytorch import GATConv


class GATLayer(nn.Module):
    def __init__(self, g, in_dim, out_dim):
        super(GATLayer, self).__init__()
        self.g = g
        # equation (1)
        self.fc = nn.Linear(in_dim, out_dim, bias=False)
        # equation (2)
        self.attn_fc = nn.Linear(2 * out_dim, 1, bias=False)
        self.reset_parameters()

    def reset_parameters(self):
        """Reinitialize learnable parameters."""
        gain = nn.init.calculate_gain("relu")
        nn.init.xavier_normal_(self.fc.weight, gain=gain)
        nn.init.xavier_normal_(self.attn_fc.weight, gain=gain)

    def edge_attention(self, edges):
        # edge UDF for equation (2)
        z2 = torch.cat([edges.src["z"], edges.dst["z"]], dim=1)
        a = self.attn_fc(z2)
        return {"e": F.leaky_relu(a)}

    def message_func(self, edges):
        # message UDF for equation (3) & (4)
        return {"z": edges.src["z"], "e": edges.data["e"]}

    def reduce_func(self, nodes):
        # reduce UDF for equation (3) & (4)
        # equation (3)
        alpha = F.softmax(nodes.mailbox["e"], dim=1)
        # equation (4)
        h = torch.sum(alpha * nodes.mailbox["z"], dim=1)
        return {"h": h}

    def forward(self, h):
        # equation (1)
        z = self.fc(h)
        self.g.ndata["z"] = z
        # equation (2)
        self.g.apply_edges(self.edge_attention)
        # equation (3) & (4)
        self.g.update_all(self.message_func, self.reduce_func)
        return self.g.ndata.pop("h")

方程 (1)

\[z_i^{(l)}=W^{(l)}h_i^{(l)},(1)\]

第一个展示了线性变换。这是常见的，并且可以很容易地在Pytorch中使用torch.nn.Linear实现。

方程 (2)

\[e_{ij}^{(l)}=\text{LeakyReLU}(\vec a^{(l)^T}(z_i^{(l)}|z_j^{(l)})),(2)\]

未归一化的注意力分数 \(e_{ij}\) 是通过相邻节点 \(i\) 和 \(j\) 的嵌入计算的。这表明注意力分数可以被视为边数据，可以通过 apply_edges API 计算。apply_edges 的参数是一个 Edge UDF，其定义如下：

def edge_attention(self, edges):
    # edge UDF for equation (2)
    z2 = torch.cat([edges.src["z"], edges.dst["z"]], dim=1)
    a = self.attn_fc(z2)
    return {"e": F.leaky_relu(a)}

在这里，使用PyTorch的线性变换attn_fc再次实现了与可学习权重向量\(\vec{a^{(l)}}\)的点积。注意，apply_edges会将所有边数据批量处理为一个张量，因此这里的cat和attn_fc是并行应用于所有边的。

方程 (3) & (4)

\[\begin{split}\begin{align} \alpha_{ij}^{(l)}&=\frac{\exp(e_{ij}^{(l)})}{\sum_{k\in \mathcal{N}(i)}^{}\exp(e_{ik}^{(l)})},&(3)\\ h_i^{(l+1)}&=\sigma\left(\sum_{j\in \mathcal{N}(i)} {\alpha^{(l)}_{ij} z^{(l)}_j }\right),&(4) \end{align}\end{split}\]

与GCN类似，update_all API用于在所有节点上触发消息传递。消息函数发送出两个张量：源节点的转换后的z嵌入和每条边上的未归一化注意力分数e。然后，reduce函数执行两个任务：

• 使用softmax归一化注意力分数（公式（3））。

• 通过注意力分数加权聚合邻居嵌入（公式(4)）。

两个任务首先从邮箱中获取数据，然后在第二个维度（dim=1）上对其进行操作，消息在该维度上进行批处理。

def reduce_func(self, nodes):
    # reduce UDF for equation (3) & (4)
    # equation (3)
    alpha = F.softmax(nodes.mailbox["e"], dim=1)
    # equation (4)
    h = torch.sum(alpha * nodes.mailbox["z"], dim=1)
    return {"h": h}

多头注意力机制

类似于ConvNet中的多个通道，GAT引入了多头注意力来丰富模型容量并稳定学习过程。每个注意力头都有自己的参数，它们的输出可以通过两种方式合并：

\[\text{concatenation}: h^{(l+1)}_{i} =||_{k=1}^{K}\sigma\left(\sum_{j\in \mathcal{N}(i)}\alpha_{ij}^{k}W^{k}h^{(l)}_{j}\right)\]

或

\[\text{average}: h_{i}^{(l+1)}=\sigma\left(\frac{1}{K}\sum_{k=1}^{K}\sum_{j\in\mathcal{N}(i)}\alpha_{ij}^{k}W^{k}h^{(l)}_{j}\right)\]

其中 \(K\) 是头的数量。你可以使用连接来处理中间层，并在最终层使用平均。

使用上述定义的单头GATLayer作为下面MultiHeadGATLayer的构建块：

class MultiHeadGATLayer(nn.Module):
    def __init__(self, g, in_dim, out_dim, num_heads, merge="cat"):
        super(MultiHeadGATLayer, self).__init__()
        self.heads = nn.ModuleList()
        for i in range(num_heads):
            self.heads.append(GATLayer(g, in_dim, out_dim))
        self.merge = merge

    def forward(self, h):
        head_outs = [attn_head(h) for attn_head in self.heads]
        if self.merge == "cat":
            # concat on the output feature dimension (dim=1)
            return torch.cat(head_outs, dim=1)
        else:
            # merge using average
            return torch.mean(torch.stack(head_outs))

将所有内容整合在一起

现在，你可以定义一个两层的GAT模型。

class GAT(nn.Module):
    def __init__(self, g, in_dim, hidden_dim, out_dim, num_heads):
        super(GAT, self).__init__()
        self.layer1 = MultiHeadGATLayer(g, in_dim, hidden_dim, num_heads)
        # Be aware that the input dimension is hidden_dim*num_heads since
        # multiple head outputs are concatenated together. Also, only
        # one attention head in the output layer.
        self.layer2 = MultiHeadGATLayer(g, hidden_dim * num_heads, out_dim, 1)

    def forward(self, h):
        h = self.layer1(h)
        h = F.elu(h)
        h = self.layer2(h)
        return h


import networkx as nx

然后我们使用DGL内置的数据模块加载Cora数据集。

from dgl import DGLGraph
from dgl.data import citation_graph as citegrh


def load_cora_data():
    data = citegrh.load_cora()
    g = data[0]
    mask = torch.BoolTensor(g.ndata["train_mask"])
    return g, g.ndata["feat"], g.ndata["label"], mask

训练循环与GCN教程中的完全相同。

import time

import numpy as np

g, features, labels, mask = load_cora_data()

# create the model, 2 heads, each head has hidden size 8
net = GAT(g, in_dim=features.size()[1], hidden_dim=8, out_dim=7, num_heads=2)

# create optimizer
optimizer = torch.optim.Adam(net.parameters(), lr=1e-3)

# main loop
dur = []
for epoch in range(30):
    if epoch >= 3:
        t0 = time.time()

    logits = net(features)
    logp = F.log_softmax(logits, 1)
    loss = F.nll_loss(logp[mask], labels[mask])

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    if epoch >= 3:
        dur.append(time.time() - t0)

    print(
        "Epoch {:05d} | Loss {:.4f} | Time(s) {:.4f}".format(
            epoch, loss.item(), np.mean(dur)
        )
    )

  NumNodes: 2708
  NumEdges: 10556
  NumFeats: 1433
  NumClasses: 7
  NumTrainingSamples: 140
  NumValidationSamples: 500
  NumTestSamples: 1000
Done loading data from cached files.
/home/ubuntu/prod-doc/readthedocs.org/user_builds/dgl/envs/latest/lib/python3.8/site-packages/numpy/core/fromnumeric.py:3464: RuntimeWarning: Mean of empty slice.
  return _methods._mean(a, axis=axis, dtype=dtype,
/home/ubuntu/prod-doc/readthedocs.org/user_builds/dgl/envs/latest/lib/python3.8/site-packages/numpy/core/_methods.py:192: RuntimeWarning: invalid value encountered in scalar divide
  ret = ret.dtype.type(ret / rcount)
Epoch 00000 | Loss 1.9431 | Time(s) nan
Epoch 00001 | Loss 1.9412 | Time(s) nan
Epoch 00002 | Loss 1.9394 | Time(s) nan
Epoch 00003 | Loss 1.9375 | Time(s) 0.1490
Epoch 00004 | Loss 1.9357 | Time(s) 0.1493
Epoch 00005 | Loss 1.9338 | Time(s) 0.1487
Epoch 00006 | Loss 1.9320 | Time(s) 0.1485
Epoch 00007 | Loss 1.9301 | Time(s) 0.1483
Epoch 00008 | Loss 1.9282 | Time(s) 0.1483
Epoch 00009 | Loss 1.9263 | Time(s) 0.1481
Epoch 00010 | Loss 1.9244 | Time(s) 0.1481
Epoch 00011 | Loss 1.9225 | Time(s) 0.1481
Epoch 00012 | Loss 1.9206 | Time(s) 0.1482
Epoch 00013 | Loss 1.9187 | Time(s) 0.1484
Epoch 00014 | Loss 1.9168 | Time(s) 0.1484
Epoch 00015 | Loss 1.9148 | Time(s) 0.1483
Epoch 00016 | Loss 1.9129 | Time(s) 0.1483
Epoch 00017 | Loss 1.9109 | Time(s) 0.1483
Epoch 00018 | Loss 1.9089 | Time(s) 0.1488
Epoch 00019 | Loss 1.9070 | Time(s) 0.1489
Epoch 00020 | Loss 1.9050 | Time(s) 0.1488
Epoch 00021 | Loss 1.9030 | Time(s) 0.1489
Epoch 00022 | Loss 1.9010 | Time(s) 0.1489
Epoch 00023 | Loss 1.8989 | Time(s) 0.1489
Epoch 00024 | Loss 1.8969 | Time(s) 0.1489
Epoch 00025 | Loss 1.8948 | Time(s) 0.1493
Epoch 00026 | Loss 1.8928 | Time(s) 0.1493
Epoch 00027 | Loss 1.8907 | Time(s) 0.1492
Epoch 00028 | Loss 1.8886 | Time(s) 0.1491
Epoch 00029 | Loss 1.8865 | Time(s) 0.1491

可视化和理解学习到的注意力

Cora

下表总结了在Cora数据集上报告的模型性能，该性能在GAT论文中报告，并通过DGL实现获得。

模型	准确率
GCN (论文)	\(81.4\pm 0.5%\)
GCN (dgl)	\(82.05\pm 0.33%\)
GAT (论文)	\(83.0\pm 0.7%\)
GAT (dgl)	\(83.69\pm 0.529%\)

我们的模型学到了什么样的注意力分布？

因为注意力权重 \(a_{ij}\) 与边相关联，你可以通过给边着色来可视化它。下面你可以选择 Cora 的一个子图并绘制最后一个 GATLayer 的注意力权重。节点根据它们的标签着色，而边根据注意力权重的大小着色，可以参考右侧的颜色条。

你可以看到模型似乎学习了不同的注意力权重。为了更彻底地理解分布，测量注意力分布的熵)。对于任何节点\(i\)，\(\{\alpha_{ij}\}_{j\in\mathcal{N}(i)}\)形成了其所有邻居的离散概率分布，其熵由以下公式给出：

\[H({\alpha_{ij}}_{j\in\mathcal{N}(i)})=-\sum_{j\in\mathcal{N}(i)} \alpha_{ij}\log\alpha_{ij}\]

低熵意味着高度集中，反之亦然。熵为0意味着所有注意力都集中在一个源节点上。均匀分布具有最高的熵\(\log(\mathcal{N}(i))\)。理想情况下，您希望看到模型学习到较低熵的分布（即，一两个邻居比其他邻居重要得多）。

请注意，由于节点的度数可能不同，最大熵也会有所不同。因此，您绘制了整个图中所有节点的熵值的聚合直方图。以下是每个注意力头学习到的注意力直方图。

作为参考，这里是所有节点具有均匀注意力权重分布的直方图。

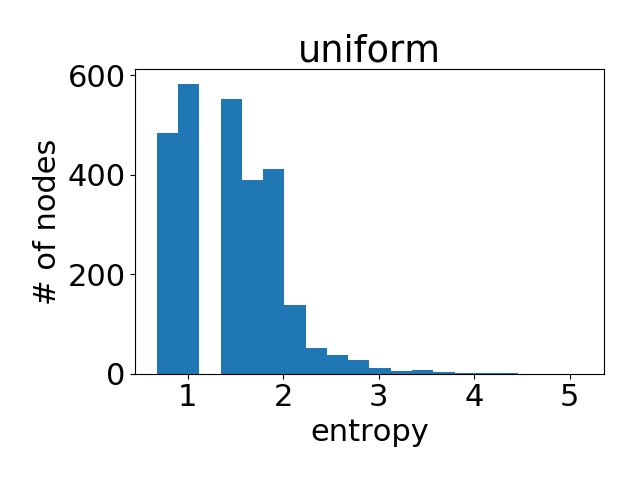
可以看出，学习到的注意力值与均匀分布非常相似 （即所有邻居同等重要）。这部分解释了为什么在Cora数据集上，GAT的性能接近GCN （根据作者报告的结果，100次运行的平均准确率差异小于2%）。注意力并不重要， 因为它没有太大的区分度。

这是否意味着注意力机制没有用？ 不！不同的数据集会展现出完全不同的模式，如下所示。

蛋白质-蛋白质相互作用（PPI）网络

这里使用的PPI数据集由\(24\)个图组成，对应于不同的人类组织。节点最多可以有\(121\)种标签，因此节点的标签表示为一个大小为\(121\)的二进制张量。任务是预测节点标签。

使用\(20\)个图进行训练，\(2\)个用于验证，\(2\)个用于测试。每个图的平均节点数为\(2372\)。每个节点具有\(50\)个特征，这些特征由位置基因集、基序基因集和免疫学特征组成。关键的是，测试图在训练期间完全未被观察到，这种设置称为“归纳学习”。

比较GAT和GCN在此任务上\(10\)次随机运行的性能，并在验证集上使用超参数搜索以找到最佳模型。

模型	F1分数（微平均）
GAT	\(0.975 \pm 0.006\)
图卷积网络	\(0.509 \pm 0.025\)
论文	\(0.973 \pm 0.002\)

上表是本次实验的结果，其中您使用微F1分数来评估模型性能。

注意

以下是F1分数的计算过程：

\[ \begin{align}\begin{aligned}precision=\frac{\sum_{t=1}^{n}TP_{t}}{\sum_{t=1}^{n}(TP_{t} +FP_{t})}\\recall=\frac{\sum_{t=1}^{n}TP_{t}}{\sum_{t=1}^{n}(TP_{t} +FN_{t})}\\F1_{micro}=2\frac{precision*recall}{precision+recall}\end{aligned}\end{align} \]

• \(TP_{t}\) 表示实际具有标签 \(t\) 并且被预测为具有标签 \(t\) 的节点数量

• \(FP_{t}\) 表示没有但被预测为具有标签 \(t\) 的节点数量

• \(FN_{t}\) 表示被标记为 \(t\) 但被预测为其他类别的输出类别数量。

• \(n\) 是标签的数量，即在我们的情况下是 \(121\)。

在训练过程中，使用BCEWithLogitsLoss作为损失函数。GAT和GCN的学习曲线如下所示；明显的是，GAT相对于GCN的性能优势显著。

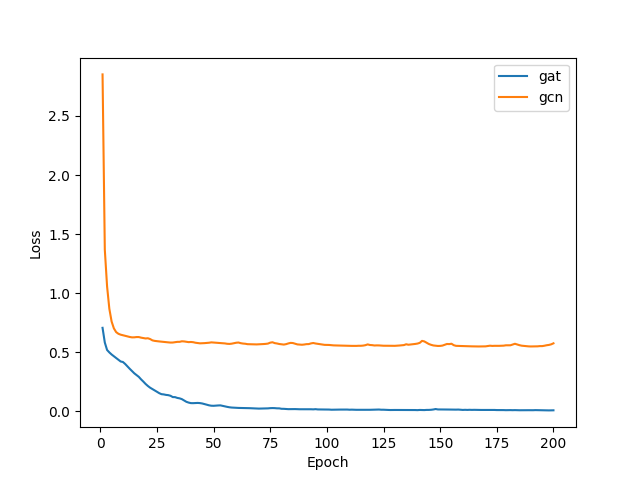
和之前一样，您可以通过显示节点注意力熵的直方图来对学习的注意力进行统计理解。以下是不同注意力层学习到的注意力直方图。

第一层学习到的注意力：

在第2层学习到的注意力：

在最后一层学到的注意力：

再次，与均匀分布进行比较：

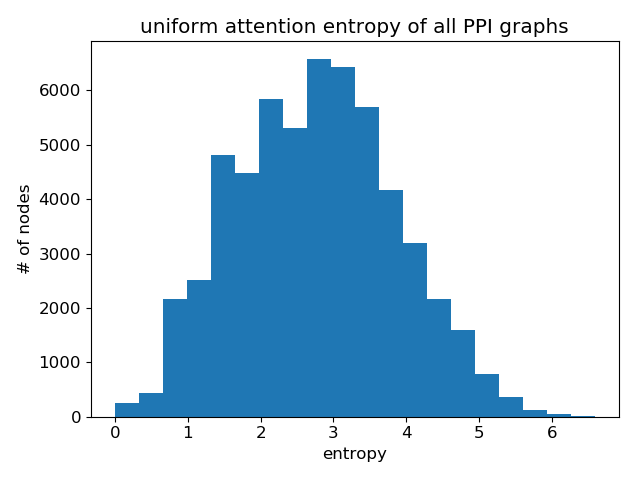
显然，GAT确实学会了锐利的注意力权重！各层之间也有一个明显的模式：随着层数的增加，注意力变得更加锐利。

与Cora数据集中GAT的增益微乎其微不同，对于PPI数据集，GAT与其他GNN变体相比在GAT论文中表现出显著的性能差距（至少20%），并且两者之间的注意力分布明显不同。虽然这值得进一步研究，但一个直接的结论是，GAT的优势可能更多地在于其处理具有更复杂邻域结构图的能力。

What’s next?

到目前为止，你已经了解了如何使用DGL来实现GAT。还有一些缺失的细节，比如dropout、跳跃连接和超参数调优，这些实践不涉及DGL相关的概念。更多信息请查看完整示例。

• 查看优化后的完整示例。

• 下一个教程描述了如何通过并行化多个注意力头和SPMV优化来加速GAT模型。