qml.measurements

警告

除非您是PennyLane或插件开发者，否则您可能不需要直接使用这些类。

查看主要测量页面以获取可用测量的详细信息。

该模块包含PennyLane支持的所有测量。

描述

测量

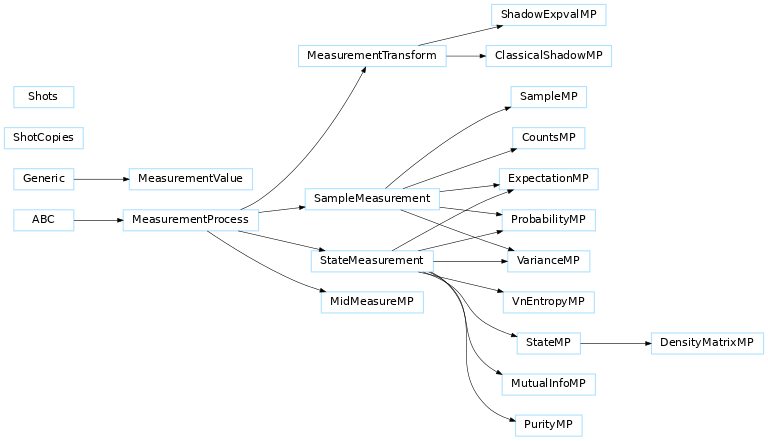
MeasurementProcess 类作为测量的基类，并由 SampleMeasurement、 StateMeasurement 和 MeasurementTransform 类继承。这些类被子类化以在 PennyLane 中实现测量。

• 每个 SampleMeasurement 子类代表一个基于样本的测量，它包含一个 SampleMeasurement.process_samples() 方法和一个 SampleMeasurement.process_counts() 方法，这些方法处理设备生成的样本序列。 process_samples 方法应该始终具有相同的参数：

  • 样本 (Sequence[complex]): 为所有导线生成的计算基样本

  • wire_order (Wires): 确定samples作用的子空间的导线

  • shot_range (tuple[int]): 指定使用的样本范围的两个整数元组。如果未指定，则使用所有样本。

  • bin_size (int)：将射击范围划分为大小为 bin_size 的区间，并分别返回每个区间的测量统计。如果未提供，则将整个射击范围视为一个单一的区间。

  SampleMeasurement.process_counts() 当前是可选的。它接受一个字典，将基态的字符串表示映射到一个整数和电线顺序。

  请参见 CountsMP 以获取示例。

• 每个 StateMeasurement 子类表示一个基于状态的测量，它包含一个 StateMeasurement.process_state() 方法，该方法处理由设备生成的量子状态。该方法应该始终具有相同的参数：

  • state (Sequence[complex]): 量子状态

  • wire_order (导线): 决定state作用的子空间的导线; 维度为\(2^n\)的矩阵作用于\(n\)个导线的子空间

  请参阅 StateMP 的示例。

• 每个 MeasurementTransform 子类代表一个需要应用批处理变换的测量过程，该变换包含一个 MeasurementTransform.process() 方法，该方法将给定的量子带转换为一批量子带，并使用设备执行它们。该方法应该始终具有相同的参数：

  • 胶带 (QuantumTape): 用于变换的量子胶带

  • 设备 (Device): 用于转换量子带的设备

  MeasurementTransform与batch_transform()之间的主要区别在于，批量转换是由梯度转换跟踪的，而MeasurementTransform过程则不是。

  有关示例，请参见 ClassicalShadowMP。

注意

一个测量过程可以同时继承自 SampleMeasurement 和 StateMeasurement 类，定义处理样本或量子状态所需的逻辑。参见 VarianceMP 以获取示例。

微分

一般来说，MeasurementProcess 对于一个参数是可微的，如果该参数的定义域是连续的。当使用解析微分方法时，测量过程的输出必须是一个实数标量值，这样才能是可微的。

处理中途测量

中途测量可以使用 qml.measure() 进行。测量值由 qml.measure 返回，可以作为经典控制的条件。此外，可以使用算术运算符组合多个测量值以进行更复杂的条件判断：

import pennylane as qml

dev = qml.device("default.qubit", wires=3)

@qml.qnode(dev)
def circ(x, y):
    qml.RX(x, wires=0)
    qml.RY(y, wires=1)

    m0 = qml.measure(0)
    m1 = qml.measure(1)
    qml.cond(~m0 & m1 == 0, qml.X)(wires=2)
    return qml.expval(qml.Z(2))

在进行中间电路测量后，导线可以照常重复使用。此外，通过将qml.measure的reset关键字参数设置为True，还可以将已测量的导线重置为\(|0 \rangle\)状态。

用户还可以收集中间电路测量以及其他终端测量的统计数据。目前，qml.expval、qml.probs、qml.sample、qml.counts和qml.var是支持的。qml.probs、qml.sample和qml.counts支持测量值的序列，qml.expval和qml.var不支持。所有的测量值的算术组合的统计数据都被支持，除了qml.probs，并且只要它们不是以序列的形式收集，例如，[m1 + m2, m1 - m2]是不支持的。

import pennylane as qml

dev = qml.device("default.qubit", wires=3)

@qml.qnode(dev)
def circ(x, y):
    qml.RX(x, wires=0)
    qml.RY(y, wires=1)
    m0 = qml.measure(1)
    return qml.expval(qml.Z(0)), qml.sample(m0)

在收集中途测量统计时，QNodes 可以像往常一样执行：

>>> circ(1.0, 2.0, shots=5)
(0.6, array([1, 1, 1, 0, 1]))

PennyLane 还支持对中途测量结果进行后选择。要了解更多信息，请参考measure()的文档。

创建自定义测量

可以通过继承上述提到的任何类来创建自定义测量过程。

以下是一个基于样本的测量示例，用于计算获得的给定状态的样本数量：

import pennylane as qml
from pennylane.measurements import SampleMeasurement

class CountState(SampleMeasurement):
    def __init__(self, state: str):
        self.state = state  # string identifying the state e.g. "0101"
        wires = list(range(len(state)))
        super().__init__(wires=wires)

    def process_samples(self, samples, wire_order, shot_range=None, bin_size=None):
        counts_mp = qml.counts(wires=self._wires)
        counts = counts_mp.process_samples(samples, wire_order, shot_range, bin_size)
        return float(counts.get(self.state, 0))

    def process_counts(self, counts, wire_order):
        return float(counts.get(self.state, 0))

    def __copy__(self):
        return CountState(state=self.state)

注意

当在 __init__ 方法中添加新参数时，需要重写 __copy__ 方法。

此示例中的测量过程使用了 counts() 函数，该函数是一个返回包含每个量子状态被采样次数的字典的测量过程。

我们现在可以在一个 QNode 中执行新的测量。让我们使用一个简单的电路，以便我们能够从数学上验证我们的结果。

dev = qml.device("default.qubit", wires=1, shots=10000)

@qml.qnode(dev)
def circuit(x):
    qml.RX(x, wires=0)
    return CountState(state="1")

测量前的量子态为：

\[\begin{split}\psi = R_x(\theta) \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} \cos(\theta/2) & -i\sin(\theta/2) \\ -i\sin(\theta/2) & \cos(\theta/2) \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} \cos(\theta/2) \\ -i\sin(\theta/2) \end{bmatrix}\end{split}\]

当 \(\theta = 1.23\) 时，获得态 \(\begin{bmatrix} 1 \\ 0 \end{bmatrix}\) 的概率是 \(\sin^2(\theta/2) = 0.333\)。使用 10000 次实验 我们大约应该获得激发态 3333 次。

>>> circuit(1.23)
array(3303.)

鉴于测量过程返回一个实数标量值，我们可以使用解析方法对其进行微分。

我们从之前的分析中知道，测量过程的解析结果是 \(r(\theta) = \text{nshots} \cdot \sin^2(\theta/2)\)。

测量过程的梯度是 \(\frac{\partial r}{\partial \theta} = \text{nshots} \sin(\theta/2) \cos(\theta/2)\).

当 \(\theta = 1.23\), \(\frac{\partial r}{\partial \theta} = 4712.444\)

>>> x = qml.numpy.array(1.23, requires_grad=True)
>>> qml.grad(circuit)(x)
4715.000000000001

注意

在PennyLane中，我们使用函数来定义测量（例如 counts()）。这些 函数将返回相应测量过程的实例 （例如 CountsMP）。这个决定仅仅是出于设计目的。

序列化和 Pytree 格式

PennyLane 测量会自动注册为 Pytrees . MeasurementProcess._flatten 和 MeasurementProcess._unflatten 需要被重写，如果测量具有附加的 元数据，例如 seed 或 all_outcomes。

>>> H = 2.0 * qml.X(0)
>>> mp = qml.expval(H)
>>> mp._flatten()
((2.0 * X(0), None), (('wires', None),))
>>> type(mp)._unflatten(*mp._flatten())
expval(2.0 * X(0))
>>> jax.tree_util.tree_leaves(mp)
[2.0]

将您的新测量添加到PennyLane

如果您想将此新测量添加到PennyLane，以便其他用户可以受益，您必须创建一个Pull Request，创建一个以您的测量名称命名的文件（例如 state.py），并将其添加到 pennylane/measurements/ 中。此文件应包含：

• 具有适当的 process 方法定义的测量类。

• 与创建的文件同名的函数，将用于实例化测量类。

测试被添加到一个类似名称和位置的文件中，位于 tests/measurements/。

这个类和这个函数需要在 pennylane/measurements/__init__.py 中导入。这个函数需要在 pennylane/__init__.py 中导入。

这里有一些关于添加测量的更多提示：

• 仔细选择名称。 好的名称告诉用户测量的用途，或它实现的架构。问问自己，是否可能在不同的上下文中添加类似名称的测量。

• 撰写良好的文档字符串。 用清晰的文档字符串解释您的测量功能，并提供充足的示例。

您可以在文档中的指南中找到有关Pennylane标准的更多信息。

概述

顶层测量函数

创建标准PennyLane测量过程的 measurements 函数是顶级导入：

classical_shadow(导线[, 种子])	经典阴影测量协议。
counts([op, wires, all_outcomes])	从提供的观测值中获取样本，样本数量由对应设备的 dev.shots 属性决定，返回每个样本的计数数量。
density_matrix(电线)	计算基中的量子密度矩阵。
expval(op)	提供的可观察量的期望值。
measure(导线[, 重置, 后选择])	对提供的量子比特进行计算基中的中途测量。
mutual_info(wires0, wires1[, log_base])	测量之前子系统之间的互信息：
probs([wires, op])	每个计算基态的概率。
purity(导线)	测量前系统的纯度。
sample([操作, 导线])	来自提供的可观察对象的样本，样本数量由相应设备的 dev.shots 属性确定，返回原始样本。
shadow_expval(H[, k, seed])	以可微分的方式使用经典阴影计算期望值。
state()	计算基中的量子态。
var(op)	提供的可观察量的方差。
vn_entropy(wires[, log_base])	测量前系统的冯·诺依曼熵。

函数

add_shots(s1, s2)	通过连接它们的射击向量来添加两个 Shots 对象。
find_post_processed_mcms(电路)	返回后处理所需的中途测量的子集。

类

ClassicalShadowMP([wires, seed, id])	表示量子变分电路末尾发生的经典阴影测量过程。
CountsMP([obs, wires, eigvals, id, all_outcomes])	从提供的可观察量中采样的测量过程，并返回每个样本的计数。
DensityMatrixMP(线路[, id])	测量过程，返回计算基上的量子状态。
ExpectationMP([观测值, 导线, 特征值, 标识符])	测量过程，计算所提供可观察量的期望值。
MeasurementProcess([obs, wires, eigvals, id])	表示在量子变分电路末尾发生的测量过程。
MeasurementTransform([obs, wires, eigvals, id])	将变换应用到给定量子带的测量过程。
MeasurementValue(measurements, processing_fn)	一个表示量子位模型中未知测量结果的类。
MidMeasureMP([wires, reset, postselect, id])	中途测量。
MutualInfoMP([wires, id, log_base])	测量过程，计算提供的线路之间的互信息。
ProbabilityMP([观测, 线圈, 特征值, 标识])	测量过程计算每个计算基态的概率。
PurityMP(导线[, id])	在测量之前计算系统纯度的测量过程。
SampleMP([obs, wires, eigvals, id])	测量过程，返回给定可观测量的样本。
SampleMeasurement([obs, wires, eigvals, id])	基于样本的测量过程。
ShadowExpvalMP(H[, seed, k, id])	利用经典影子测量过程测量算子的期望值。
ShotCopies(shots, copies)	一个命名元组，表示一种数量被重复一定次数。
Shots([shots])	一个存储拍摄信息的数据类。
StateMP([导线, 标识])	测量过程，返回计算基上的量子状态。
StateMeasurement([obs, wires, eigvals, id])	基于状态的测量过程。
VarianceMP([obs, wires, eigvals, id])	计算提供的可观测量的方差的测量过程。
VnEntropyMP([wires, id, log_base])	测量过程，用于计算测量前系统的冯·诺依曼熵。

变量

AllCounts	枚举类，用于表示可观察对象的返回类型。
Counts	枚举类用于表示可观察对象的返回类型。
期望	枚举类，用于表示可观测对象的返回类型。
MidMeasure	枚举类，用于表示可观察对象的返回类型。
MutualInfo	枚举类，用于表示可观察对象的返回类型。
概率	枚举类用于表示可观察对象的返回类型。
纯度	枚举类，用于表示可观察对象的返回类型。
示例	枚举类，用于表示可观察对象的返回类型。
Shadow	枚举类，用于表示可观测对象的返回类型。
ShadowExpval	枚举类，用于表示可观测对象的返回类型。
State	枚举类，用于表示可观察对象的返回类型。
方差	枚举类，用于表示可观察对象的返回类型。
VnEntropy	枚举类用于表示可观察对象的返回类型。

类继承图

代码/qml_测量

 

下载 Python 脚本

 

下载笔记本

 

在GitHub上查看