统计估计和误差条#

数据可视化有时涉及聚合或估计的步骤，其中多个数据点被简化为一个汇总统计量，如均值或中位数。当显示汇总统计量时，通常适合添加 误差条 ，这提供了关于汇总统计量如何代表基础数据点的视觉提示。

seaborn 的几个函数在给定完整数据集时会自动计算汇总统计数据和误差线。本章解释了如何控制误差线的显示内容，以及为什么您可能会选择 seaborn 提供的每个选项。

围绕集中趋势估计的误差线可以显示两种一般情况之一：要么是估计的不确定性范围，要么是基础数据围绕它的分布。这些度量是相关的：在相同的样本量下，当数据分布更广时，估计会更加不确定。但随着样本量的增加，不确定性会减少，而分布不会。

在 seaborn 中，构建每种误差条有两种方法。一种方法是参数化的，使用依赖于分布形状假设的公式。另一种方法是非参数化的，仅使用您提供的数据。

你的选择是通过 errorbar 参数做出的，该参数存在于每个作为绘图一部分进行估计的函数中。此参数接受要使用的方法名称，并可选地接受一个控制区间大小的参数。选择可以在一个二维分类中定义，该分类取决于显示的内容及其构建方式：

../_images/error_bars_2_0.svg

您会注意到，参数方法和非参数方法的 size 参数定义不同。对于参数误差条，它是一个标量因子，乘以定义误差的统计量（标准误差或标准差）。对于非参数误差条，它是一个百分位宽度。下面将进一步解释每种特定方法。

备注

这里描述的 errorbar API 是在 seaborn v0.12 中引入的。在之前的版本中，唯一的选择是显示一个引导置信区间或标准差，选择由 ci 参数控制（即 ci=<size> 或 ci="sd"）。

为了比较不同的参数化，我们将使用以下辅助函数：

def plot_errorbars(arg, **kws):
    np.random.seed(sum(map(ord, "error_bars")))
    x = np.random.normal(0, 1, 100)
    f, axs = plt.subplots(2, figsize=(7, 2), sharex=True, layout="tight")
    sns.pointplot(x=x, errorbar=arg, **kws, capsize=.3, ax=axs[0])
    sns.stripplot(x=x, jitter=.3, ax=axs[1])

数据分散的度量#

表示数据分布的误差条提供了一种紧凑的分布显示方式，使用三个数字，而 boxplot() 需要5个或更多数字，violinplot() 则需要一个复杂的算法。

标准偏差误差线#

标准差误差棒是最容易解释的，因为标准差是一个熟悉的统计量。它是每个数据点到样本均值的平均距离。默认情况下，errorbar="sd" 将在估计值周围绘制 +/- 1 标准差的误差棒，但可以通过传递一个缩放大小参数来增加范围。请注意，假设数据呈正态分布，约 68% 的数据将位于一个标准差内，约 95% 将位于两个标准差内，约 99.7% 将位于三个标准差内：

plot_errorbars("sd")
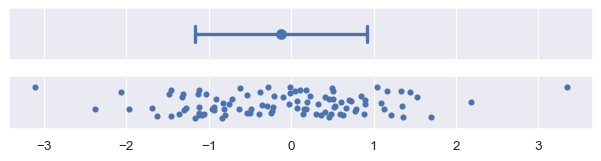
../_images/error_bars_6_0.png

百分位区间误差条#

百分位区间也代表数据落入的某个范围，但它们是通过直接从样本中计算这些百分位数来实现的。默认情况下，errorbar="pi" 将显示一个95%的区间，范围从2.5到97.5百分位数。你可以通过传递一个大小参数来选择不同的范围，例如，显示四分位距：

plot_errorbars(("pi", 50))
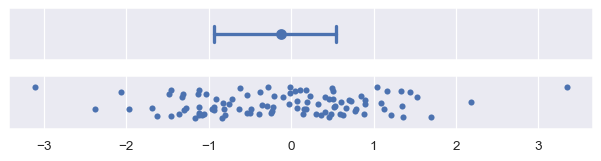
../_images/error_bars_8_0.png

标准差误差条将始终对称地围绕估计值。当数据偏斜时，这可能是一个问题，特别是当存在自然界限时（例如，如果数据代表一个只能为正的数量）。在某些情况下，标准差误差条可能会延伸到“不可能”的值。非参数方法没有这个问题，因为它可以考虑不对称的分布，并且永远不会超出数据的范围。

估计不确定性的度量#

如果你的数据是从一个更大的总体中随机抽取的样本，那么均值（或其他估计值）将是总体真实平均值的不完美度量。显示估计不确定性的误差条试图表示真实参数的可能值范围。

标准误差条#

标准误差统计量与标准差有关：实际上，它只是标准差除以样本大小的平方根。默认情况下，使用 errorbar="se" 时，会在均值的上下绘制一个标准误差的区间：

plot_errorbars("se")
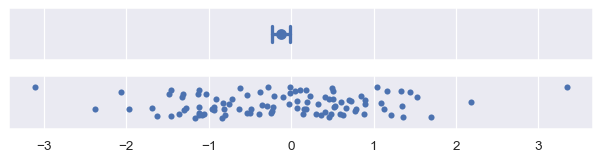
../_images/error_bars_11_0.png

置信区间误差条#

非参数方法表示不确定性的方式使用 bootstrapping：一种过程，其中数据集被随机重采样多次，并且每次重采样后重新计算估计值。这个过程创建了一个统计分布，近似于如果你有不同的样本，你可能得到的估计值的分布。

置信区间是通过取*bootstrap分布*的百分位区间构建的。默认情况下，`errorbar=”ci”`绘制一个95%的置信区间：

plot_errorbars("ci")
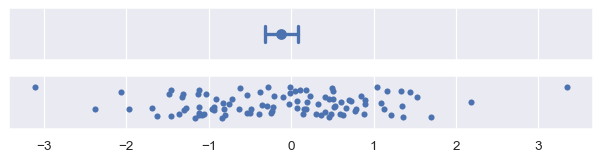
../_images/error_bars_13_0.png

seaborn 的术语有些特定，因为在统计学中，置信区间可以是参数化的或非参数化的。要绘制一个参数化的置信区间，你可以使用类似于上面提到的公式来缩放标准误差。例如，一个近似的 95% 置信区间可以通过取均值 +/- 两个标准误差来构建：

plot_errorbars(("se", 2))
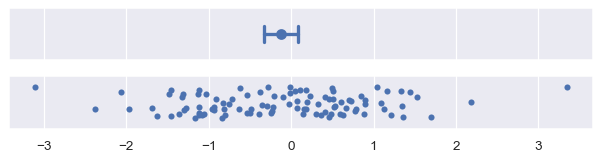
../_images/error_bars_15_0.png

非参数自助法具有与百分位区间类似的优点：它自然地适应于偏斜和有界数据，这是标准误差区间无法做到的。它也更加通用。虽然标准误差公式是针对均值的，但可以使用自助法为任何估计量计算误差条。

plot_errorbars("ci", estimator="median")
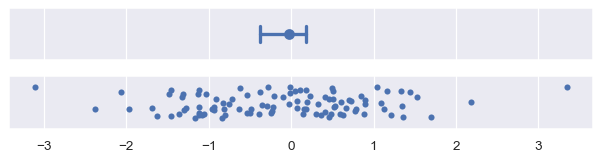
../_images/error_bars_17_0.png

Bootstrapping 涉及随机性，每次运行生成它们的代码时，误差条都会略有不同。有几个参数控制这一点。一个参数设置迭代次数（n_boot）：迭代次数越多，结果区间将越稳定。另一个参数设置随机数生成器的 seed，这将确保结果相同：

plot_errorbars("ci", n_boot=5000, seed=10)
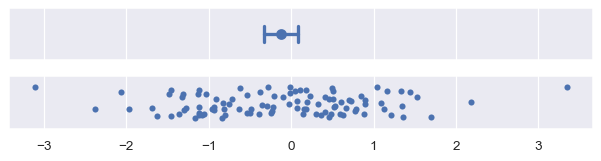
../_images/error_bars_19_0.png

由于其迭代过程，引导区间（bootstrap intervals）的计算可能会非常昂贵，尤其是在处理大数据集时。但由于不确定性随样本量减少，在这种情况下，使用代表数据分布的误差条可能更具信息量。

自定义误差条#

如果这些方法不够用，也可以将一个通用函数传递给 errorbar 参数。这个函数应该接受一个向量并生成一对值，表示区间的最小值和最大值：

plot_errorbars(lambda x: (x.min(), x.max()))
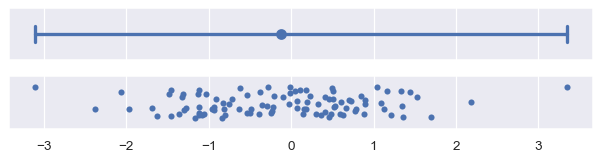
../_images/error_bars_21_0.png

（实际上，你可以使用 errorbar=("pi", 100) 来展示数据的完整范围，而不是上面展示的自定义函数）。

需要注意的是，seaborn 函数目前无法从外部计算的值中绘制误差条，尽管可以使用 matplotlib 函数将此类误差条添加到 seaborn 图中。

回归拟合的误差条#

前面的讨论主要集中在围绕聚合数据参数估计显示的误差线上。在seaborn中，当估计回归模型以可视化关系时，也会出现误差线。在这里，误差线将由回归线周围的“带”表示：

x = np.random.normal(0, 1, 50)
y = x * 2 + np.random.normal(0, 2, size=x.size)
sns.regplot(x=x, y=y)
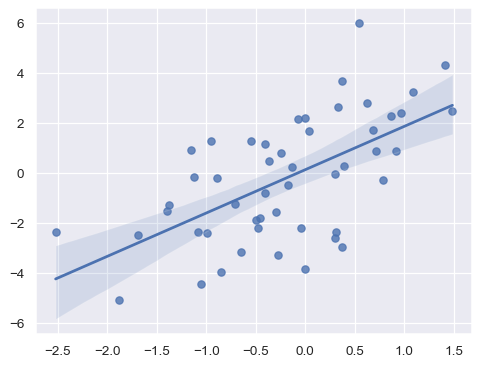
../_images/error_bars_24_0.png

目前，回归估计的误差条不太灵活，仅显示通过 ci= 设置大小的置信区间。这在未来可能会改变。

误差棒足够吗？#

你应该总是问自己，是否最好使用一个只显示汇总统计量和误差条的图表。在许多情况下，并非如此。

如果你对总结性问题感兴趣（例如，均值在不同组之间是否不同或随时间增加），聚合可以简化图形的复杂性，使这些推断更容易。但这样做的同时，它会掩盖关于基础数据点的有价值信息，例如分布的形状和异常值的存在。

在分析自己的数据时，不要满足于汇总统计。也要始终查看基础分布。有时，将这两种视角结合到同一图中会很有帮助。许多 seaborn 函数可以协助完成这项任务，特别是那些在 分类教程 中讨论的函数。