估计回归拟合#

许多数据集包含多个定量变量，分析的目标通常是找出这些变量之间的关系。我们 之前讨论过 可以通过显示两个变量的联合分布来实现这一点的函数。然而，使用统计模型来估计两个噪声观测集之间的简单关系是非常有帮助的。本章中讨论的函数将通过线性回归的通用框架来实现这一点。

在Tukey的精神指导下，seaborn中的回归图主要用于添加视觉指南，以帮助在探索性数据分析期间强调数据集中的模式。也就是说，seaborn本身并不是一个统计分析包。要获得与回归模型拟合相关的定量测量，您应该使用 statsmodels。然而，seaborn的目标是通过可视化快速简便地探索数据集，因为这样做与通过统计表格探索数据集同样（如果不是更重要的话）重要。

用于绘制线性回归模型的函数#

可以用来可视化线性拟合的两个函数是 regplot() 和 lmplot()。

在最简单的调用中，这两个函数都会绘制两个变量 x 和 y 的散点图，然后拟合回归模型 y ~ x 并绘制得到的回归线和该回归的95%置信区间：

tips = sns.load_dataset("tips")
sns.regplot(x="total_bill", y="tip", data=tips);
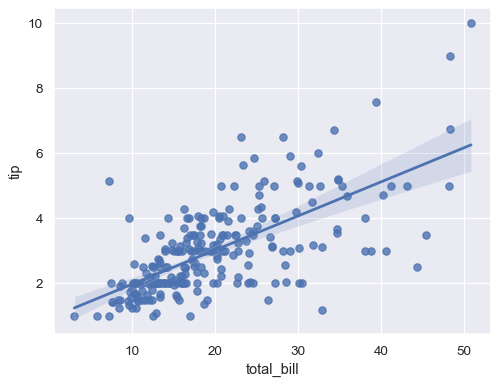
../_images/regression_4_0.png 
sns.lmplot(x="total_bill", y="tip", data=tips);
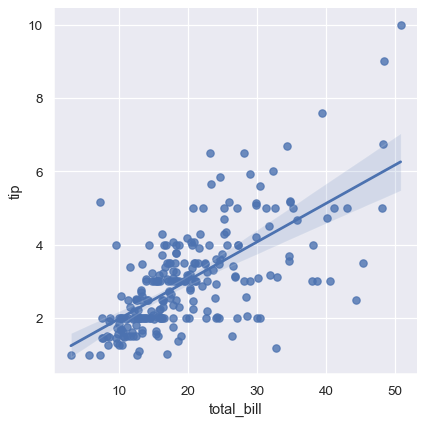
../_images/regression_5_0.png

这些函数绘制相似的图形，但 regplot() 是一个 轴级函数，而 lmplot() 是一个图形级函数。此外，regplot() 接受 x 和 y 变量在多种格式中，包括简单的 numpy 数组、pandas.Series 对象，或作为传递给 data 的 pandas.DataFrame 对象中的变量引用。相比之下，lmplot() 将 data 作为必需参数，并且 x 和 y 变量必须指定为字符串。最后，只有 lmplot() 具有 hue 作为参数。

核心功能在其他方面是相似的，因此本教程将重点介绍 lmplot():

当其中一个变量取离散值时，可以进行线性回归，然而，这种数据集生成的简单散点图通常不是最优的：

sns.lmplot(x="size", y="tip", data=tips);
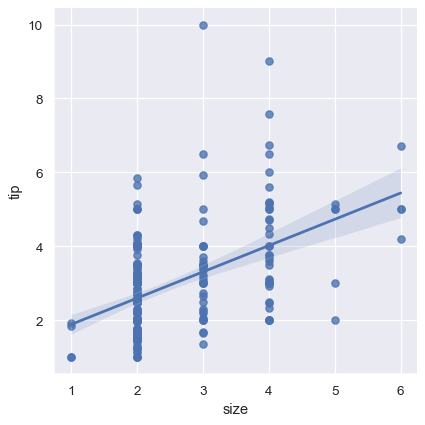
../_images/regression_7_0.png

一种选择是向离散值添加一些随机噪声（“抖动”），以使这些值的分布更加清晰。请注意，抖动仅应用于散点图数据，并不影响回归线本身的拟合：

sns.lmplot(x="size", y="tip", data=tips, x_jitter=.05);
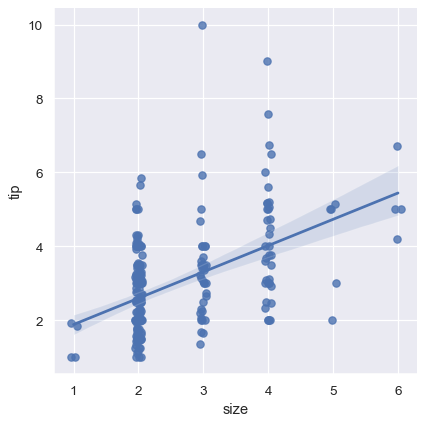
../_images/regression_9_0.png

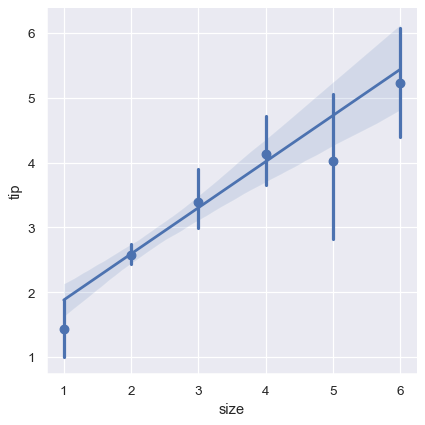
第二个选项是折叠每个离散区间内的观测值，以绘制中心趋势的估计值以及置信区间：

sns.lmplot(x="size", y="tip", data=tips, x_estimator=np.mean);
../_images/regression_11_0.png

拟合不同类型的模型#

上面使用的简单线性回归模型非常容易拟合，然而，它并不适用于某些类型的数据集。Anscombe’s quartet 数据集展示了一些例子，其中简单线性回归提供了相同的关系估计，而简单的视觉检查显然显示了差异。例如，在第一种情况下，线性回归是一个好的模型：

anscombe = sns.load_dataset("anscombe")

sns.lmplot(x="x", y="y", data=anscombe.query("dataset == 'I'"),
           ci=None, scatter_kws={"s": 80});
../_images/regression_14_0.png

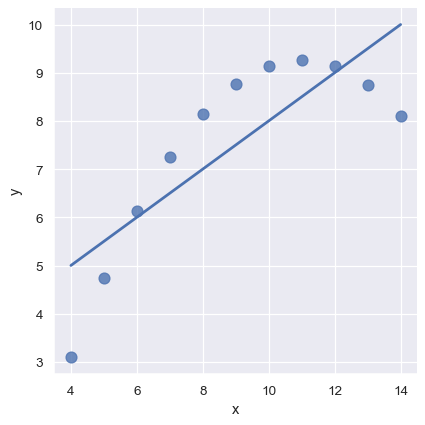
第二个数据集中的线性关系是相同的，但图表清楚地显示这不是一个好的模型：

sns.lmplot(x="x", y="y", data=anscombe.query("dataset == 'II'"),
           ci=None, scatter_kws={"s": 80});
../_images/regression_16_0.png

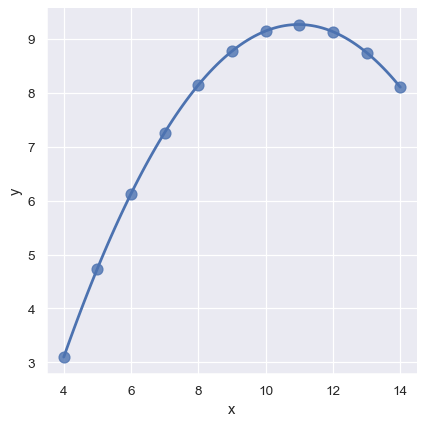
在这些高阶关系的背景下，lmplot() 和 regplot() 可以拟合多项式回归模型，以探索数据集中简单的非线性趋势：

sns.lmplot(x="x", y="y", data=anscombe.query("dataset == 'II'"),
           order=2, ci=None, scatter_kws={"s": 80});
../_images/regression_18_0.png

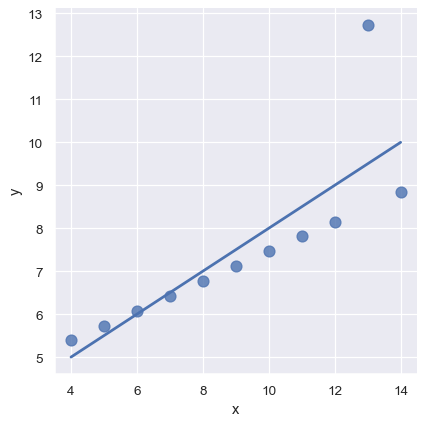
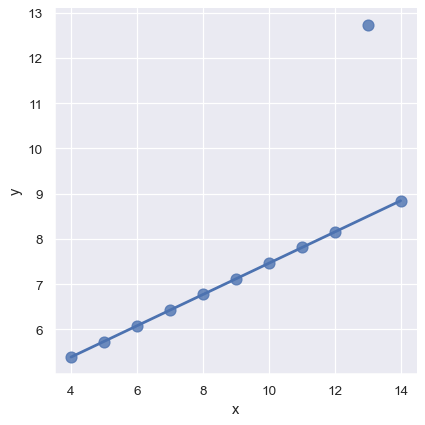
另一个问题是“异常值”观测，这些观测由于某些原因偏离了研究中的主要关系：

sns.lmplot(x="x", y="y", data=anscombe.query("dataset == 'III'"),
           ci=None, scatter_kws={"s": 80});
../_images/regression_20_0.png

在存在异常值的情况下，拟合一个稳健回归可能会有用，这种回归使用不同的损失函数来降低相对较大的残差的影响：

sns.lmplot(x="x", y="y", data=anscombe.query("dataset == 'III'"),
           robust=True, ci=None, scatter_kws={"s": 80});
../_images/regression_22_0.png

当 y 变量是二进制时，简单线性回归虽然“有效”，但提供的预测结果并不可信：

tips["big_tip"] = (tips.tip / tips.total_bill) > .15
sns.lmplot(x="total_bill", y="big_tip", data=tips,
           y_jitter=.03);
../_images/regression_24_0.png

在这种情况下，解决方案是拟合一个逻辑回归，使得回归线显示给定 x 值时 y = 1 的估计概率：

sns.lmplot(x="total_bill", y="big_tip", data=tips,
           logistic=True, y_jitter=.03);
../_images/regression_26_0.png

请注意，逻辑回归估计在计算上要复杂得多（这也适用于稳健回归）。由于回归线周围的置信区间是使用bootstrap程序计算的，您可能希望关闭此功能以加快迭代速度（使用 ci=None）。

另一种完全不同的方法是使用 lowess smoother 进行非参数回归。这种方法的假设最少，尽管它在计算上非常密集，因此目前根本不计算置信区间：

sns.lmplot(x="total_bill", y="tip", data=tips,
           lowess=True, line_kws={"color": "C1"});
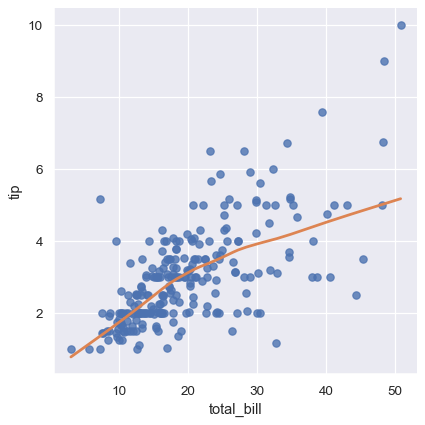
../_images/regression_28_0.png

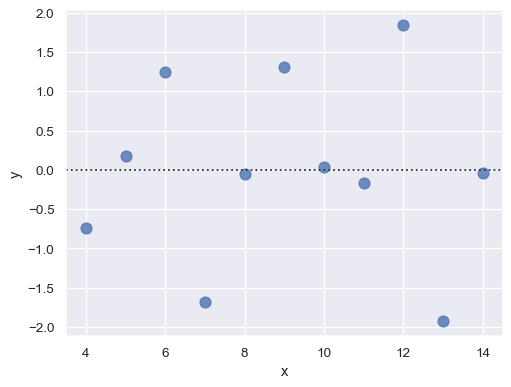
函数 residplot() 可以是一个有用的工具，用于检查简单回归模型是否适合某个数据集。它拟合并移除一个简单线性回归，然后绘制每个观测值的残差值。理想情况下，这些值应该随机分布在 y = 0 周围：

sns.residplot(x="x", y="y", data=anscombe.query("dataset == 'I'"),
              scatter_kws={"s": 80});
../_images/regression_30_0.png

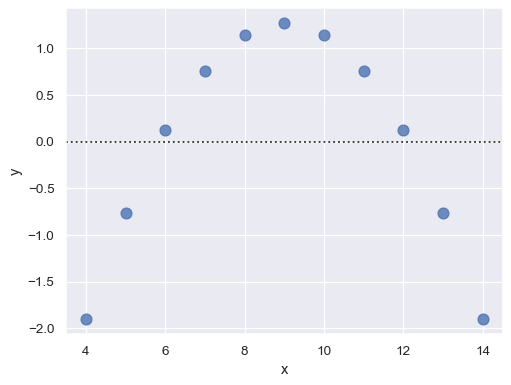
如果残差中存在结构，这表明简单线性回归可能不合适：

sns.residplot(x="x", y="y", data=anscombe.query("dataset == 'II'"),
              scatter_kws={"s": 80});
../_images/regression_32_0.png

基于其他变量进行条件化#

上面的图表展示了探索一对变量之间关系的多种方法。然而，通常一个更有趣的问题是“这两个变量之间的关系如何随着第三个变量的变化而变化？”这就是 regplot() 和 lmplot() 的主要区别所在。虽然 regplot() 总是显示单一的关系，但 lmplot() 结合了 regplot() 和 FacetGrid 来使用 hue 映射或分面显示多个拟合。

分离关系的最佳方式是在同一坐标轴上绘制两个级别，并使用颜色来区分它们：

sns.lmplot(x="total_bill", y="tip", hue="smoker", data=tips);
../_images/regression_34_0.png

与 relplot() 不同，无法将不同的变量映射到散点图的样式属性，但可以通过标记形状冗余地编码 hue 变量：

sns.lmplot(x="total_bill", y="tip", hue="smoker", data=tips,
           markers=["o", "x"], palette="Set1");
../_images/regression_36_0.png

要添加另一个变量，您可以通过在网格的行或列中显示变量的每个级别来绘制多个“方面”：

sns.lmplot(x="total_bill", y="tip", hue="smoker", col="time", data=tips);
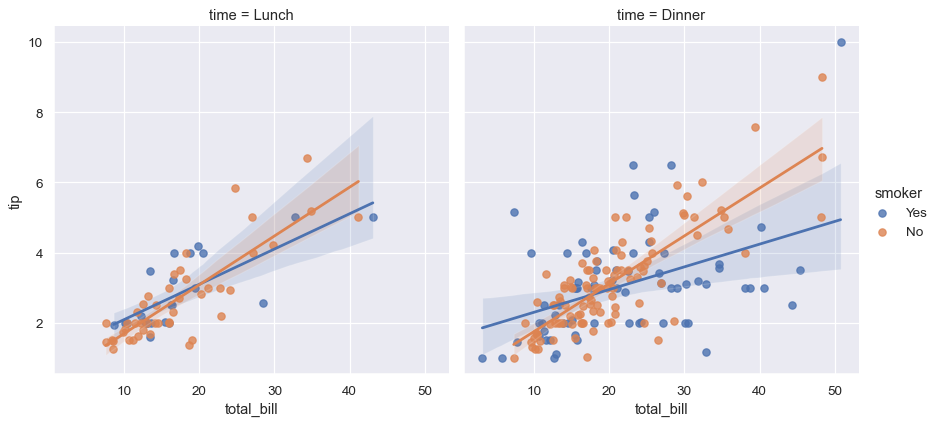
../_images/regression_38_0.png 
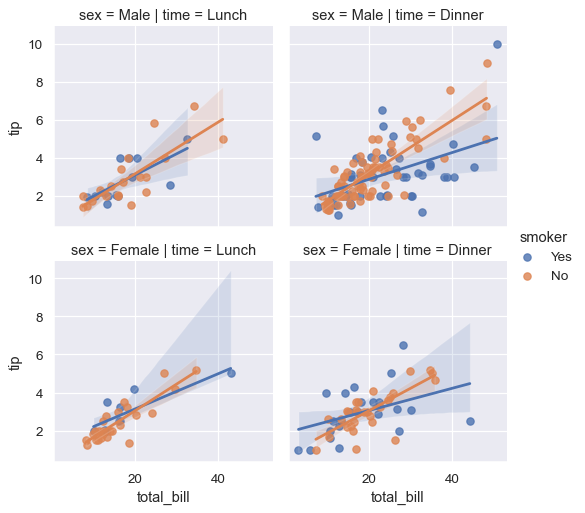
sns.lmplot(x="total_bill", y="tip", hue="smoker",
           col="time", row="sex", data=tips, height=3);
../_images/regression_39_0.png

在其他情境中绘制回归图#

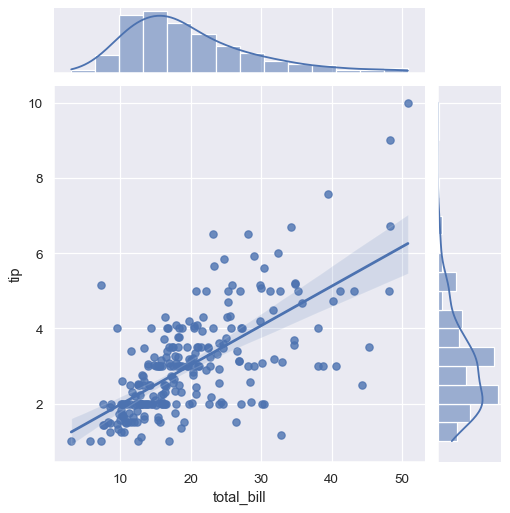
一些其他的seaborn函数在更大、更复杂的图表环境中使用了 regplot()。首先是我们在 分布教程 中介绍的 jointplot() 函数。除了之前讨论的绘图样式外， jointplot() 可以通过传递 kind="reg" 来使用 regplot() 在联合轴上显示线性回归拟合：

sns.jointplot(x="total_bill", y="tip", data=tips, kind="reg");
../_images/regression_41_0.png

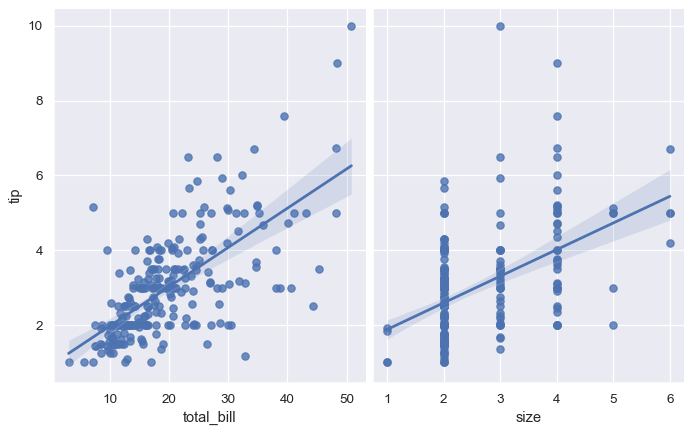
使用 pairplot() 函数并设置 kind="reg" 可以将 regplot() 和 PairGrid 结合起来，展示数据集中变量之间的线性关系。请注意这与 lmplot() 的区别。在下图中，两个轴并没有展示在第三个变量的两个水平下相同的关系；相反，PairGrid() 用于展示数据集中不同变量对之间的多个关系：

sns.pairplot(tips, x_vars=["total_bill", "size"], y_vars=["tip"],
             height=5, aspect=.8, kind="reg");
../_images/regression_43_0.png

通过 hue 参数，这两个函数都可以内置对附加分类变量的条件处理：

sns.pairplot(tips, x_vars=["total_bill", "size"], y_vars=["tip"],
             hue="smoker", height=5, aspect=.8, kind="reg");
../_images/regression_45_0.png