statsmodels.graphics.functional.hdrboxplot

statsmodels.graphics.functional.hdrboxplot(data, ncomp=2, alpha=None, threshold=0.95, bw=None, xdata=None, labels=None, ax=None, use_brute=False, seed=None)[source]

高密度区域箱线图

Parameters:
datasequence of ndarrays or 2-D ndarray

用于创建功能箱线图的函数向量。如果是一个1-D数组的序列，这些数组的大小应该相同。第一个轴是函数索引，第二个轴是函数定义的轴。因此 data[0, :] 是第一个功能曲线。

ncompint, optional

要使用的组件数量。如果为 None，则返回数据中行数或列数较小的那个数量。

alphalist of floats between 0 and 1, optional

额外要计算的分位数值。默认是 None

thresholdfloat between 0 and 1, optional

用于异常值检测的百分位阈值。较高的值意味着对异常值的敏感度较低。默认值为 0.95。

bwarray_like or str, optional

如果是一个数组，它是用户指定的固定带宽。如果是None，则设置为normal_reference。如果是一个字符串，应该是以下之一：

  • normal_reference: 正常参考经验法则（默认）

  • cv_ml: 交叉验证最大似然

  • cv_ls: 交叉验证最小二乘法

xdatandarray, optional

数据的独立变量。如果没有给出，则假设为整数数组 0..N-1，其中 N 是 data 中向量的长度。

labelssequence of scalar or str, optional

曲线在数据中的标签或标识符。如果未给出，异常值在图中会用数组索引进行标记。

axAxesSubplot, optional

如果指定，此子图将用于绘图，而不是创建新图形。

use_brutebool

使用蛮力优化器而不是默认的差分进化来寻找曲线。默认为False。

seed{None, int, np.random.RandomState}

传递给 scipy.optimize.differential_evolution 的种子值。可以是整数或 RandomState 实例。如果为 None，则使用 np.random 提供的默认 RandomState。

Returns:
figFigure

如果 ax 为 None，则创建图形。否则为 ax 连接的图形。

hdr_resHdrResults instance

一个具有以下属性的HdrResults实例：

  • ‘中位数’, 数组。中位数曲线。

  • ‘hdr_50’, 数组。50%分位数带。[上界, 下界]曲线

  • ‘hdr_90’, list of array. 90% quantile band. [sup, inf]

    曲线。

  • ‘extra_quantiles’, list of array. Extra quantile band.

    [上确界, 下确界]曲线。

  • ‘outliers’, ndarray. 异常曲线。

另请参阅

banddepth, rainbowplot, fboxplot

注释

中位曲线是在主成分分析（PCA）的降维空间中具有最高概率的曲线。

离群值被定义为落在由阈值给定的分位数对应的带之外的曲线。

非异常区域定义为由所有非异常曲线组成的带状区域。

在幕后，数据集被表示为一个矩阵。每一行对应一个一维曲线。然后使用主成分分析（PCA）对该矩阵进行分解。这允许使用有限数量的模式或成分来表示数据。这种压缩过程可以将函数的表示转换为矩阵的标量表示。换句话说，您可以根据其成分可视化每条曲线。因此，每条曲线在这个简化空间中是一个点。如果有2个成分，这被称为二元图（2D图）。

在这个图中，如果某些点是相邻的（相似的成分），这意味着在原始空间中，曲线是相似的。然后，找到中位曲线意味着在降维空间中找到高密度区域（HDR）。此外，你离这个HDR越远，曲线与其他曲线的相似性就越低。

使用核平滑技术，可以恢复多元空间的概率密度函数（PDF）。从该PDF中，可以计算与点簇相关的密度概率并绘制其等高线。

最后，使用这些轮廓，可以提取不同的分位数以及中位曲线和异常值。

生成HDR箱线图的步骤包括：

  1. 计算多元核密度估计

  2. 计算90%、50%和alpha%分位数的等高线

  3. 绘制二元图

  4. 计算中位数曲线以及分位数和异常值曲线。

参考文献

[1] R.J. Hyndman and H.L. Shang, “Rainbow Plots, Bagplots, and Boxplots for

功能数据”，第19卷，第29-45页，2010年。

示例

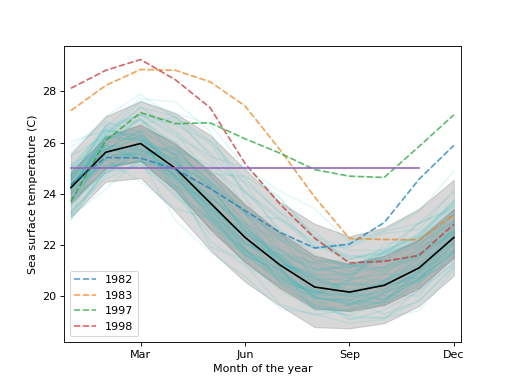
加载厄尔尼诺数据集。包含60年太平洋海洋海面温度数据。

>>> import matplotlib.pyplot as plt
>>> import statsmodels.api as sm
>>> data = sm.datasets.elnino.load()

创建一个功能性箱线图。我们看到1982-83年和1997-98年是异常值；这些年份是厄尔尼诺现象（一种以海面温度升高和气压升高为特征的气候模式）以异常强度发生的年份。

>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> res = sm.graphics.hdrboxplot(data.raw_data[:, 1:],
...                              labels=data.raw_data[:, 0].astype(int),
...                              ax=ax)

>>> ax.set_xlabel("Month of the year")
>>> ax.set_ylabel("Sea surface temperature (C)")
>>> ax.set_xticks(np.arange(13, step=3) - 1)
>>> ax.set_xticklabels(["", "Mar", "Jun", "Sep", "Dec"])
>>> ax.set_xlim([-0.2, 11.2])

>>> plt.show()

(源代码, png, 高分辨率png, pdf)

../_images/graphics_functional_hdrboxplot_00_00.png
Last update: Oct 16, 2024