注意
跳至末尾 下载完整示例代码。
融合Softmax¶
在本教程中,您将编写一个融合的softmax操作,对于特定类别的矩阵(那些行可以放入GPU的SRAM中的矩阵),该操作比PyTorch原生操作要快得多。
在此过程中,您将了解:
内核融合对带宽受限操作的优势。
Triton中的归约运算符。
动机¶
针对元素级加法定制GPU内核在教学上很有价值,但在实践中作用有限。 让我们转而考虑一个简单的(数值稳定的)softmax运算案例:
import torch
import triton
import triton.language as tl
from triton.runtime import driver
DEVICE = triton.runtime.driver.active.get_active_torch_device()
def is_hip():
return triton.runtime.driver.active.get_current_target().backend == "hip"
def is_cdna():
return is_hip() and triton.runtime.driver.active.get_current_target().arch in ('gfx940', 'gfx941', 'gfx942',
'gfx90a', 'gfx908')
def naive_softmax(x):
"""Compute row-wise softmax of X using native pytorch
We subtract the maximum element in order to avoid overflows. Softmax is invariant to
this shift.
"""
# read MN elements ; write M elements
x_max = x.max(dim=1)[0]
# read MN + M elements ; write MN elements
z = x - x_max[:, None]
# read MN elements ; write MN elements
numerator = torch.exp(z)
# read MN elements ; write M elements
denominator = numerator.sum(dim=1)
# read MN + M elements ; write MN elements
ret = numerator / denominator[:, None]
# in total: read 5MN + 2M elements ; wrote 3MN + 2M elements
return ret
在PyTorch中原始实现时,计算y = naive_softmax(x)对于\(x \in R^{M \times N}\)
需要从DRAM读取\(5MN + 2M\)个元素并写回\(3MN + 2M\)个元素。
这显然效率低下;我们更希望有一个自定义的"融合"内核,只需读取
X一次并在芯片上完成所有必要的计算。
这样做只需要读写\(MN\)字节,因此我们
可以预期理论加速比约为4倍(即\((8MN + 4M) / 2MN\))。
torch.jit.script标志旨在自动执行这种"内核融合",
但正如我们稍后将看到的,它仍然远非理想。
计算内核¶
我们的softmax内核工作流程如下:每个程序加载输入矩阵X的一组行,按程序数量进行跨步访问,对其进行归一化处理,然后将结果写回输出Y。
需要注意的是,Triton的一个重要限制是每个块必须包含2的幂次方数量的元素,因此如果我们想要处理任何可能的输入形状,就需要在内部对每行进行"填充"并妥善保护内存操作:
@triton.jit
def softmax_kernel(output_ptr, input_ptr, input_row_stride, output_row_stride, n_rows, n_cols, BLOCK_SIZE: tl.constexpr,
num_stages: tl.constexpr):
# starting row of the program
row_start = tl.program_id(0)
row_step = tl.num_programs(0)
for row_idx in tl.range(row_start, n_rows, row_step, num_stages=num_stages):
# The stride represents how much we need to increase the pointer to advance 1 row
row_start_ptr = input_ptr + row_idx * input_row_stride
# The block size is the next power of two greater than n_cols, so we can fit each
# row in a single block
col_offsets = tl.arange(0, BLOCK_SIZE)
input_ptrs = row_start_ptr + col_offsets
# Load the row into SRAM, using a mask since BLOCK_SIZE may be > than n_cols
mask = col_offsets < n_cols
row = tl.load(input_ptrs, mask=mask, other=-float('inf'))
# Subtract maximum for numerical stability
row_minus_max = row - tl.max(row, axis=0)
# Note that exponentiation in Triton is fast but approximate (i.e., think __expf in CUDA)
numerator = tl.exp(row_minus_max)
denominator = tl.sum(numerator, axis=0)
softmax_output = numerator / denominator
# Write back output to DRAM
output_row_start_ptr = output_ptr + row_idx * output_row_stride
output_ptrs = output_row_start_ptr + col_offsets
tl.store(output_ptrs, softmax_output, mask=mask)
我们可以创建一个辅助函数,用于为任何给定的输入张量入队内核及其(元)参数。
properties = driver.active.utils.get_device_properties(DEVICE.index)
NUM_SM = properties["multiprocessor_count"]
NUM_REGS = properties["max_num_regs"]
SIZE_SMEM = properties["max_shared_mem"]
WARP_SIZE = properties["warpSize"]
target = triton.runtime.driver.active.get_current_target()
kernels = {}
def softmax(x):
n_rows, n_cols = x.shape
# The block size of each loop iteration is the smallest power of two greater than the number of columns in `x`
BLOCK_SIZE = triton.next_power_of_2(n_cols)
# Another trick we can use is to ask the compiler to use more threads per row by
# increasing the number of warps (`num_warps`) over which each row is distributed.
# You will see in the next tutorial how to auto-tune this value in a more natural
# way so you don't have to come up with manual heuristics yourself.
num_warps = 8
# Number of software pipelining stages.
num_stages = 4 if SIZE_SMEM > 200000 else 2
# Allocate output
y = torch.empty_like(x)
# pre-compile kernel to get register usage and compute thread occupancy.
kernel = softmax_kernel.warmup(y, x, x.stride(0), y.stride(0), n_rows, n_cols, BLOCK_SIZE=BLOCK_SIZE,
num_stages=num_stages, num_warps=num_warps, grid=(1, ))
kernel._init_handles()
n_regs = kernel.n_regs
size_smem = kernel.metadata.shared
if is_hip():
# NUM_REGS represents the number of regular purpose registers. On CDNA architectures this is half of all registers available.
# However, this is not always the case. In most cases all registers can be used as regular purpose registers.
# ISA SECTION (3.6.4 for CDNA3)
# VGPRs are allocated out of two pools: regular VGPRs and accumulation VGPRs. Accumulation VGPRs are used
# with matrix VALU instructions, and can also be loaded directly from memory. A wave may have up to 512 total
# VGPRs, 256 of each type. When a wave has fewer than 512 total VGPRs, the number of each type is flexible - it is
# not required to be equal numbers of both types.
if is_cdna():
NUM_GPRS = NUM_REGS * 2
# MAX_NUM_THREADS represents maximum number of resident threads per multi-processor.
# When we divide this number with WARP_SIZE we get maximum number of waves that can
# execute on a CU (multi-processor) in parallel.
MAX_NUM_THREADS = properties["max_threads_per_sm"]
max_num_waves = MAX_NUM_THREADS // WARP_SIZE
occupancy = min(NUM_GPRS // WARP_SIZE // n_regs, max_num_waves) // num_warps
else:
occupancy = NUM_REGS // (n_regs * WARP_SIZE * num_warps)
occupancy = min(occupancy, SIZE_SMEM // size_smem)
num_programs = NUM_SM * occupancy
num_programs = min(num_programs, n_rows)
# Create a number of persistent programs.
kernel[(num_programs, 1, 1)](y, x, x.stride(0), y.stride(0), n_rows, n_cols, BLOCK_SIZE, num_stages)
return y
单元测试¶
我们确保在具有不规则行数和列数的矩阵上测试我们的内核。 这将使我们能够验证我们的填充机制是否正常工作。
torch.manual_seed(0)
x = torch.randn(1823, 781, device=DEVICE)
y_triton = softmax(x)
y_torch = torch.softmax(x, axis=1)
assert torch.allclose(y_triton, y_torch), (y_triton, y_torch)
正如预期的那样,结果是相同的。
基准测试¶
这里我们将以输入矩阵的列数作为变量进行性能基准测试——假设行数为4096。
然后将其性能与以下两者进行比较:(1) torch.softmax 和 (2) 上文定义的 naive_softmax。
@triton.testing.perf_report(
triton.testing.Benchmark(
x_names=['N'], # argument names to use as an x-axis for the plot
x_vals=[128 * i for i in range(2, 100)], # different possible values for `x_name`
line_arg='provider', # argument name whose value corresponds to a different line in the plot
line_vals=['triton', 'torch'], # possible values for `line_arg``
line_names=[
"Triton",
"Torch",
], # label name for the lines
styles=[('blue', '-'), ('green', '-')], # line styles
ylabel="GB/s", # label name for the y-axis
plot_name="softmax-performance", # name for the plot. Used also as a file name for saving the plot.
args={'M': 4096}, # values for function arguments not in `x_names` and `y_name`
))
def benchmark(M, N, provider):
x = torch.randn(M, N, device=DEVICE, dtype=torch.float32)
stream = getattr(torch, DEVICE.type).Stream()
getattr(torch, DEVICE.type).set_stream(stream)
if provider == 'torch':
ms = triton.testing.do_bench(lambda: torch.softmax(x, axis=-1))
if provider == 'triton':
ms = triton.testing.do_bench(lambda: softmax(x))
gbps = lambda ms: 2 * x.numel() * x.element_size() * 1e-9 / (ms * 1e-3)
return gbps(ms)
benchmark.run(show_plots=True, print_data=True)
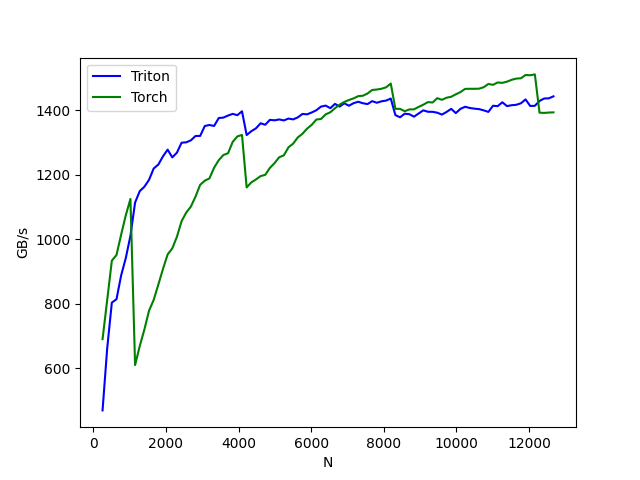
softmax-performance:
N Triton Torch
0 256.0 469.792103 690.479590
1 384.0 662.029674 811.735767
2 512.0 803.774048 933.690037
3 640.0 814.259863 951.310147
4 768.0 887.911139 1014.347900
5 896.0 941.744268 1074.276345
6 1024.0 1010.800111 1124.934718
7 1152.0 1113.810347 610.240230
8 1280.0 1149.105964 669.038125
9 1408.0 1162.764033 720.335250
10 1536.0 1184.085504 778.828310
11 1664.0 1219.239818 812.094662
12 1792.0 1231.477099 859.448345
13 1920.0 1256.886294 908.037628
14 2048.0 1277.718663 952.991168
15 2176.0 1253.725125 971.816070
16 2304.0 1268.320104 1007.719434
17 2432.0 1299.124105 1055.950085
18 2560.0 1300.365139 1082.730090
19 2688.0 1306.441687 1101.276232
20 2816.0 1319.990833 1132.168186
21 2944.0 1320.216423 1168.636828
22 3072.0 1350.997882 1181.619245
23 3200.0 1354.016834 1188.581583
24 3328.0 1351.098643 1221.780127
25 3456.0 1375.607968 1245.063417
26 3584.0 1376.988531 1261.092737
27 3712.0 1383.343078 1266.593209
28 3840.0 1388.555439 1301.730701
29 3968.0 1384.456602 1318.622662
30 4096.0 1396.556181 1323.277671
31 4224.0 1322.864751 1160.559436
32 4352.0 1334.810748 1176.315840
33 4480.0 1343.671592 1185.310404
34 4608.0 1359.287808 1195.690748
35 4736.0 1354.841830 1199.656322
36 4864.0 1369.997335 1221.139101
37 4992.0 1368.520261 1235.965433
38 5120.0 1371.279527 1254.102085
39 5248.0 1368.179618 1260.120516
40 5376.0 1373.936688 1284.889451
41 5504.0 1371.394573 1296.271412
42 5632.0 1377.587344 1315.503658
43 5760.0 1388.353173 1326.814807
44 5888.0 1387.030627 1342.728182
45 6016.0 1392.844652 1354.678115
46 6144.0 1399.846496 1370.978600
47 6272.0 1411.031522 1372.748209
48 6400.0 1414.164291 1386.946932
49 6528.0 1406.208670 1393.551380
50 6656.0 1419.471920 1405.945793
51 6784.0 1411.009759 1417.065023
52 6912.0 1421.251436 1425.455983
53 7040.0 1413.784194 1431.433972
54 7168.0 1421.633392 1436.439611
55 7296.0 1426.018564 1443.456418
56 7424.0 1421.495264 1444.651309
57 7552.0 1418.828284 1451.538160
58 7680.0 1427.975392 1462.513487
59 7808.0 1422.943836 1463.951685
60 7936.0 1427.397610 1466.297458
61 8064.0 1429.727475 1470.760793
62 8192.0 1435.952633 1482.562485
63 8320.0 1384.598040 1403.984147
64 8448.0 1377.945445 1404.082355
65 8576.0 1389.102853 1396.690335
66 8704.0 1387.508845 1402.348581
67 8832.0 1379.882152 1402.550067
68 8960.0 1389.749201 1410.167114
69 9088.0 1399.457750 1416.924510
70 9216.0 1395.016691 1424.998244
71 9344.0 1394.858859 1423.694109
72 9472.0 1392.206411 1437.172627
73 9600.0 1386.286661 1432.117636
74 9728.0 1394.420457 1438.556933
75 9856.0 1404.129055 1441.527918
76 9984.0 1390.927497 1449.154442
77 10112.0 1404.100537 1456.021603
78 10240.0 1410.556721 1465.939824
79 10368.0 1406.774314 1466.218845
80 10496.0 1404.666444 1466.183818
81 10624.0 1403.211702 1466.628643
82 10752.0 1399.436409 1471.135428
83 10880.0 1394.578227 1481.226466
84 11008.0 1413.670671 1478.431178
85 11136.0 1412.445292 1485.894046
86 11264.0 1424.475331 1484.586567
87 11392.0 1412.601028 1488.308142
88 11520.0 1415.350157 1494.075980
89 11648.0 1416.603651 1497.847659
90 11776.0 1421.355225 1498.840731
91 11904.0 1433.294484 1508.954920
92 12032.0 1412.955256 1508.118766
93 12160.0 1413.539787 1510.814239
94 12288.0 1428.464053 1392.213394
95 12416.0 1436.145762 1391.470332
96 12544.0 1436.673855 1392.656796
97 12672.0 1442.793392 1393.179870
- In the above plot, we can see that:
Triton比Torch JIT快4倍。这证实了我们的怀疑,即Torch JIT在这里没有进行任何融合优化。
Triton明显比
torch.softmax更快——而且更易读、易懂和维护。 但请注意PyTorch的softmax操作更通用,可以在任何形状的张量上工作。
脚本总运行时间: (0 分钟 23.177 秒)