注意
跳至末尾 下载完整示例代码。
矩阵乘法¶
在本教程中,您将编写一个非常简短的高性能FP16矩阵乘法内核,其性能可与cuBLAS或rocBLAS相媲美。
您将具体学习以下内容:
块级矩阵乘法。
多维指针运算。
程序重新排序以提高L2缓存命中率。
自动性能调优。
动机¶
矩阵乘法是现代高性能计算系统中的关键构建模块。 众所周知它们难以优化,因此其实现通常由硬件供应商自己完成,作为所谓的"内核库"(如cuBLAS)的一部分。 不幸的是,这些库通常是专有的,无法轻松定制以满足现代深度学习工作负载的需求(例如融合激活函数)。 在本教程中,您将学习如何使用Triton自行实现高效的矩阵乘法,这种方法既易于定制又易于扩展。
大致来说,我们将编写的内核将实现以下分块算法来将一个 (M, K) 矩阵与一个 (K, N) 矩阵相乘:
# Do in parallel for m in range(0, M, BLOCK_SIZE_M): # Do in parallel for n in range(0, N, BLOCK_SIZE_N): acc = zeros((BLOCK_SIZE_M, BLOCK_SIZE_N), dtype=float32) for k in range(0, K, BLOCK_SIZE_K): a = A[m : m+BLOCK_SIZE_M, k : k+BLOCK_SIZE_K] b = B[k : k+BLOCK_SIZE_K, n : n+BLOCK_SIZE_N] acc += dot(a, b) C[m : m+BLOCK_SIZE_M, n : n+BLOCK_SIZE_N] = acc
其中双重嵌套for循环的每次迭代都由一个专用的Triton程序实例执行。
计算内核¶
上述算法在Triton中实现实际上相当简单。
主要难点在于计算内循环中需要读取的A和B块的内存位置。为此,我们需要进行多维指针运算。
指针运算¶
对于一个行优先的2D张量X,X[i, j]的内存位置由
&X[i, j] = X + i*stride_xi + j*stride_xj给出。
因此,A[m : m+BLOCK_SIZE_M, k:k+BLOCK_SIZE_K]和
B[k : k+BLOCK_SIZE_K, n : n+BLOCK_SIZE_N]的指针块可以用伪代码定义为:
&A[m : m+BLOCK_SIZE_M, k:k+BLOCK_SIZE_K] = a_ptr + (m : m+BLOCK_SIZE_M)[:, None]*A.stride(0) + (k : k+BLOCK_SIZE_K)[None, :]*A.stride(1); &B[k : k+BLOCK_SIZE_K, n:n+BLOCK_SIZE_N] = b_ptr + (k : k+BLOCK_SIZE_K)[:, None]*B.stride(0) + (n : n+BLOCK_SIZE_N)[None, :]*B.stride(1);
这意味着A和B块的指针可以在Triton中初始化(即k=0)为以下代码。还需注意的是,我们需要额外的模运算来处理M不是BLOCK_SIZE_M的倍数或N不是BLOCK_SIZE_N倍数的情况,这种情况下我们可以用一些无用的值填充数据,这些值不会对结果产生影响。对于K维度,我们稍后将使用掩码加载语义来处理。
offs_am = (pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)) % M offs_bn = (pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)) % N offs_k = tl.arange(0, BLOCK_SIZE_K) a_ptrs = a_ptr + (offs_am[:, None]*stride_am + offs_k [None, :]*stride_ak) b_ptrs = b_ptr + (offs_k [:, None]*stride_bk + offs_bn[None, :]*stride_bn)
然后在内部循环中按如下方式更新:
a_ptrs += BLOCK_SIZE_K * stride_ak; b_ptrs += BLOCK_SIZE_K * stride_bk;
L2缓存优化¶
如上所述,每个程序实例计算一个[BLOCK_SIZE_M, BLOCK_SIZE_N]的C块。需要记住的是,这些块的计算顺序确实很重要,因为它会影响我们程序的L2缓存命中率,而遗憾的是,简单的行主序排序
pid = tl.program_id(axis=0) grid_n = tl.cdiv(N, BLOCK_SIZE_N) pid_m = pid // grid_n pid_n = pid % grid_n
这根本行不通。
一种可能的解决方案是以促进数据重用的顺序启动块。
这可以通过在切换到下一列之前将块按GROUP_M行进行"超级分组"来实现:
# Program ID pid = tl.program_id(axis=0) # Number of program ids along the M axis num_pid_m = tl.cdiv(M, BLOCK_SIZE_M) # Number of programs ids along the N axis num_pid_n = tl.cdiv(N, BLOCK_SIZE_N) # Number of programs in group num_pid_in_group = GROUP_SIZE_M * num_pid_n # Id of the group this program is in group_id = pid // num_pid_in_group # Row-id of the first program in the group first_pid_m = group_id * GROUP_SIZE_M # If `num_pid_m` isn't divisible by `GROUP_SIZE_M`, the last group is smaller group_size_m = min(num_pid_m - first_pid_m, GROUP_SIZE_M) # *Within groups*, programs are ordered in a column-major order # Row-id of the program in the *launch grid* pid_m = first_pid_m + ((pid % num_pid_in_group) % group_size_m) # Col-id of the program in the *launch grid* pid_n = (pid % num_pid_in_group) // group_size_m
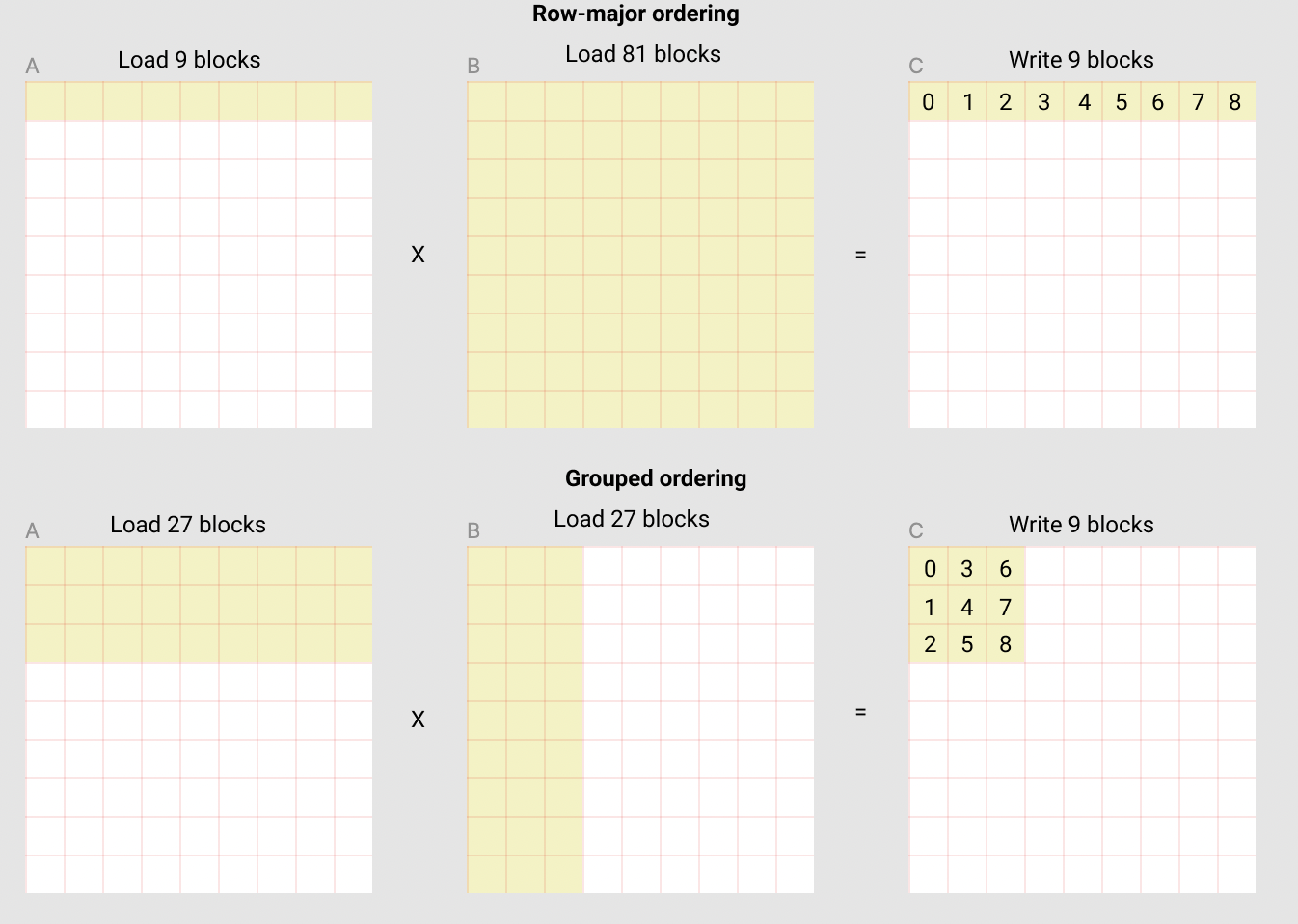
例如,在下面的矩阵乘法中,每个矩阵由9x9个块组成, 我们可以看到如果按行优先顺序计算输出,需要将90个块加载到SRAM中才能计算前9个输出块, 但如果采用分组顺序计算,则只需加载54个块。
在实际应用中,这可以将我们的矩阵乘法内核性能提升超过10%,具体取决于硬件架构(例如在A100上从220 TFLOPS提升至245 TFLOPS)。
最终结果¶
import torch
import triton
import triton.language as tl
DEVICE = triton.runtime.driver.active.get_active_torch_device()
def is_cuda():
return triton.runtime.driver.active.get_current_target().backend == "cuda"
def is_hip_cdna2():
target = triton.runtime.driver.active.get_current_target()
return target.backend == 'hip' and target.arch == 'gfx90a'
def get_cuda_autotune_config():
return [
triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 256, 'BLOCK_SIZE_K': 64, 'GROUP_SIZE_M': 8}, num_stages=3,
num_warps=8),
triton.Config({'BLOCK_SIZE_M': 64, 'BLOCK_SIZE_N': 256, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 128, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 64, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 64, 'BLOCK_SIZE_N': 128, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 32, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 64, 'BLOCK_SIZE_N': 32, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=5,
num_warps=2),
triton.Config({'BLOCK_SIZE_M': 32, 'BLOCK_SIZE_N': 64, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8}, num_stages=5,
num_warps=2),
# Good config for fp8 inputs.
triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 256, 'BLOCK_SIZE_K': 128, 'GROUP_SIZE_M': 8}, num_stages=3,
num_warps=8),
triton.Config({'BLOCK_SIZE_M': 256, 'BLOCK_SIZE_N': 128, 'BLOCK_SIZE_K': 128, 'GROUP_SIZE_M': 8}, num_stages=3,
num_warps=8),
triton.Config({'BLOCK_SIZE_M': 256, 'BLOCK_SIZE_N': 64, 'BLOCK_SIZE_K': 128, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 64, 'BLOCK_SIZE_N': 256, 'BLOCK_SIZE_K': 128, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 128, 'BLOCK_SIZE_K': 128, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 64, 'BLOCK_SIZE_K': 64, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 64, 'BLOCK_SIZE_N': 128, 'BLOCK_SIZE_K': 64, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4),
triton.Config({'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 32, 'BLOCK_SIZE_K': 64, 'GROUP_SIZE_M': 8}, num_stages=4,
num_warps=4)
]
def get_hip_autotune_config():
return [
triton.Config(
{'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 256, 'BLOCK_SIZE_K': 16, 'GROUP_SIZE_M': 1, 'waves_per_eu': 2},
num_warps=4, num_stages=2),
triton.Config(
{'BLOCK_SIZE_M': 256, 'BLOCK_SIZE_N': 256, 'BLOCK_SIZE_K': 16, 'GROUP_SIZE_M': 4, 'waves_per_eu': 2},
num_warps=8, num_stages=2),
triton.Config(
{'BLOCK_SIZE_M': 128, 'BLOCK_SIZE_N': 128, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 1, 'waves_per_eu': 2},
num_warps=8, num_stages=2),
triton.Config(
{'BLOCK_SIZE_M': 64, 'BLOCK_SIZE_N': 128, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 8, 'waves_per_eu': 3},
num_warps=4, num_stages=2),
triton.Config(
{'BLOCK_SIZE_M': 64, 'BLOCK_SIZE_N': 64, 'BLOCK_SIZE_K': 32, 'GROUP_SIZE_M': 1, 'waves_per_eu': 8},
num_warps=4, num_stages=2),
]
def get_autotune_config():
if is_cuda():
return get_cuda_autotune_config()
else:
return get_hip_autotune_config()
# `triton.jit`'ed functions can be auto-tuned by using the `triton.autotune` decorator, which consumes:
# - A list of `triton.Config` objects that define different configurations of
# meta-parameters (e.g., `BLOCK_SIZE_M`) and compilation options (e.g., `num_warps`) to try
# - An auto-tuning *key* whose change in values will trigger evaluation of all the
# provided configs
@triton.autotune(
configs=get_autotune_config(),
key=['M', 'N', 'K'],
)
@triton.jit
def matmul_kernel(
# Pointers to matrices
a_ptr, b_ptr, c_ptr,
# Matrix dimensions
M, N, K,
# The stride variables represent how much to increase the ptr by when moving by 1
# element in a particular dimension. E.g. `stride_am` is how much to increase `a_ptr`
# by to get the element one row down (A has M rows).
stride_am, stride_ak, #
stride_bk, stride_bn, #
stride_cm, stride_cn,
# Meta-parameters
BLOCK_SIZE_M: tl.constexpr, BLOCK_SIZE_N: tl.constexpr, BLOCK_SIZE_K: tl.constexpr, #
GROUP_SIZE_M: tl.constexpr, #
ACTIVATION: tl.constexpr #
):
"""Kernel for computing the matmul C = A x B.
A has shape (M, K), B has shape (K, N) and C has shape (M, N)
"""
# -----------------------------------------------------------
# Map program ids `pid` to the block of C it should compute.
# This is done in a grouped ordering to promote L2 data reuse.
# See above `L2 Cache Optimizations` section for details.
pid = tl.program_id(axis=0)
num_pid_m = tl.cdiv(M, BLOCK_SIZE_M)
num_pid_n = tl.cdiv(N, BLOCK_SIZE_N)
num_pid_in_group = GROUP_SIZE_M * num_pid_n
group_id = pid // num_pid_in_group
first_pid_m = group_id * GROUP_SIZE_M
group_size_m = min(num_pid_m - first_pid_m, GROUP_SIZE_M)
pid_m = first_pid_m + ((pid % num_pid_in_group) % group_size_m)
pid_n = (pid % num_pid_in_group) // group_size_m
# ----------------------------------------------------------
# Create pointers for the first blocks of A and B.
# We will advance this pointer as we move in the K direction
# and accumulate
# `a_ptrs` is a block of [BLOCK_SIZE_M, BLOCK_SIZE_K] pointers
# `b_ptrs` is a block of [BLOCK_SIZE_K, BLOCK_SIZE_N] pointers
# See above `Pointer Arithmetic` section for details
offs_am = (pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)) % M
offs_bn = (pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)) % N
offs_k = tl.arange(0, BLOCK_SIZE_K)
a_ptrs = a_ptr + (offs_am[:, None] * stride_am + offs_k[None, :] * stride_ak)
b_ptrs = b_ptr + (offs_k[:, None] * stride_bk + offs_bn[None, :] * stride_bn)
# -----------------------------------------------------------
# Iterate to compute a block of the C matrix.
# We accumulate into a `[BLOCK_SIZE_M, BLOCK_SIZE_N]` block
# of fp32 values for higher accuracy.
# `accumulator` will be converted back to fp16 after the loop.
accumulator = tl.zeros((BLOCK_SIZE_M, BLOCK_SIZE_N), dtype=tl.float32)
for k in range(0, tl.cdiv(K, BLOCK_SIZE_K)):
# Load the next block of A and B, generate a mask by checking the K dimension.
# If it is out of bounds, set it to 0.
a = tl.load(a_ptrs, mask=offs_k[None, :] < K - k * BLOCK_SIZE_K, other=0.0)
b = tl.load(b_ptrs, mask=offs_k[:, None] < K - k * BLOCK_SIZE_K, other=0.0)
# We accumulate along the K dimension.
accumulator = tl.dot(a, b, accumulator)
# Advance the ptrs to the next K block.
a_ptrs += BLOCK_SIZE_K * stride_ak
b_ptrs += BLOCK_SIZE_K * stride_bk
# You can fuse arbitrary activation functions here
# while the accumulator is still in FP32!
if ACTIVATION == "leaky_relu":
accumulator = leaky_relu(accumulator)
c = accumulator.to(tl.float16)
# -----------------------------------------------------------
# Write back the block of the output matrix C with masks.
offs_cm = pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)
offs_cn = pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)
c_ptrs = c_ptr + stride_cm * offs_cm[:, None] + stride_cn * offs_cn[None, :]
c_mask = (offs_cm[:, None] < M) & (offs_cn[None, :] < N)
tl.store(c_ptrs, c, mask=c_mask)
# We can fuse `leaky_relu` by providing it as an `ACTIVATION` meta-parameter in `matmul_kernel`.
@triton.jit
def leaky_relu(x):
return tl.where(x >= 0, x, 0.01 * x)
我们现在可以创建一个便捷的包装函数,它只需要接收两个输入张量,并执行以下操作:(1)检查任何形状约束;(2)分配输出;(3)启动上述内核。
def matmul(a, b, activation=""):
# Check constraints.
assert a.shape[1] == b.shape[0], "Incompatible dimensions"
assert a.is_contiguous(), "Matrix A must be contiguous"
M, K = a.shape
K, N = b.shape
# Allocates output.
c = torch.empty((M, N), device=a.device, dtype=torch.float16)
# 1D launch kernel where each block gets its own program.
grid = lambda META: (triton.cdiv(M, META['BLOCK_SIZE_M']) * triton.cdiv(N, META['BLOCK_SIZE_N']), )
matmul_kernel[grid](
a, b, c, #
M, N, K, #
a.stride(0), a.stride(1), #
b.stride(0), b.stride(1), #
c.stride(0), c.stride(1), #
ACTIVATION=activation #
)
return c
单元测试¶
我们可以将自定义的矩阵乘法操作与原生torch实现(即cuBLAS)进行对比测试。
torch.manual_seed(0)
a = torch.randn((512, 512), device=DEVICE, dtype=torch.float16)
b = torch.randn((512, 512), device=DEVICE, dtype=torch.float16)
triton_output = matmul(a, b)
torch_output = torch.matmul(a, b)
print(f"triton_output_with_fp16_inputs={triton_output}")
print(f"torch_output_with_fp16_inputs={torch_output}")
# Bigger tolerance for AMD CDNA2 devices.
# CDNA2 devices use reduced precision fp16 and bf16 and flush input and
# output denormal values to zero. Detailed info is at: https://pytorch.org/docs/stable/notes/numerical_accuracy.html#reduced-precision-fp16-and-bf16-gemms-and-convolutions-on-amd-instinct-mi200-devices
rtol = 1e-2 if is_hip_cdna2() else 0
if torch.allclose(triton_output, torch_output, atol=1e-2, rtol=rtol):
print("✅ Triton and Torch match")
else:
print("❌ Triton and Torch differ")
TORCH_HAS_FP8 = hasattr(torch, "float8_e5m2")
if TORCH_HAS_FP8 and is_cuda():
torch.manual_seed(0)
a = torch.randn((512, 512), device=DEVICE, dtype=torch.float16)
b = torch.randn((512, 512), device=DEVICE, dtype=torch.float16)
a = a.to(torch.float8_e5m2)
# pre-transpose b for efficiency.
b = b.T
b = b.to(torch.float8_e5m2)
triton_output = matmul(a, b)
torch_output = torch.matmul(a.to(torch.float16), b.to(torch.float16))
print(f"triton_output_with_fp8_inputs={triton_output}")
print(f"torch_output_with_fp8_inputs={torch_output}")
if torch.allclose(triton_output, torch_output, atol=0.125, rtol=0):
print("✅ Triton and Torch match")
else:
print("❌ Triton and Torch differ")
triton_output_with_fp16_inputs=tensor([[-10.9531, -4.7109, 15.6953, ..., -28.4062, 4.3320, -26.4219],
[ 26.8438, 10.0469, -5.4297, ..., -11.2969, -8.5312, 30.7500],
[-13.2578, 15.8516, 18.0781, ..., -21.7656, -8.6406, 10.2031],
...,
[ 40.2812, 18.6094, -25.6094, ..., -2.7598, -3.2441, 41.0000],
[ -6.1211, -16.8281, 4.4844, ..., -21.0312, 24.7031, 15.0234],
[-17.0938, -19.0000, -0.3831, ..., 21.5469, -30.2344, -13.2188]],
device='cuda:0', dtype=torch.float16)
torch_output_with_fp16_inputs=tensor([[-10.9531, -4.7109, 15.6953, ..., -28.4062, 4.3320, -26.4219],
[ 26.8438, 10.0469, -5.4297, ..., -11.2969, -8.5312, 30.7500],
[-13.2578, 15.8516, 18.0781, ..., -21.7656, -8.6406, 10.2031],
...,
[ 40.2812, 18.6094, -25.6094, ..., -2.7598, -3.2441, 41.0000],
[ -6.1211, -16.8281, 4.4844, ..., -21.0312, 24.7031, 15.0234],
[-17.0938, -19.0000, -0.3831, ..., 21.5469, -30.2344, -13.2188]],
device='cuda:0', dtype=torch.float16)
✅ Triton and Torch match
triton_output_with_fp8_inputs=tensor([[-21.4375, 13.1719, 6.0352, ..., 28.7031, 8.6719, -40.7500],
[ 10.0000, 37.0000, -5.5664, ..., 20.9844, 46.8125, 30.8281],
[ 19.5625, -3.0078, -20.0469, ..., -2.1309, -8.0625, 12.5625],
...,
[-18.1562, -34.1562, -27.4219, ..., -27.3906, -24.0938, -12.3516],
[ -3.3945, -8.6250, -23.6562, ..., -4.1094, -3.5332, -16.0781],
[-23.9688, -3.2637, -33.6875, ..., 17.3125, -36.6250, 25.8594]],
device='cuda:0', dtype=torch.float16)
torch_output_with_fp8_inputs=tensor([[-21.4375, 13.1719, 6.0352, ..., 28.7031, 8.6719, -40.7500],
[ 10.0000, 37.0000, -5.5664, ..., 20.9844, 46.8125, 30.8281],
[ 19.5625, -3.0078, -20.0469, ..., -2.1309, -8.0625, 12.5625],
...,
[-18.1562, -34.1562, -27.4219, ..., -27.3906, -24.0938, -12.3516],
[ -3.3945, -8.6250, -23.6562, ..., -4.1094, -3.5332, -16.0781],
[-23.9688, -3.2637, -33.6875, ..., 17.3125, -36.6250, 25.8594]],
device='cuda:0', dtype=torch.float16)
✅ Triton and Torch match
基准测试¶
方阵性能¶
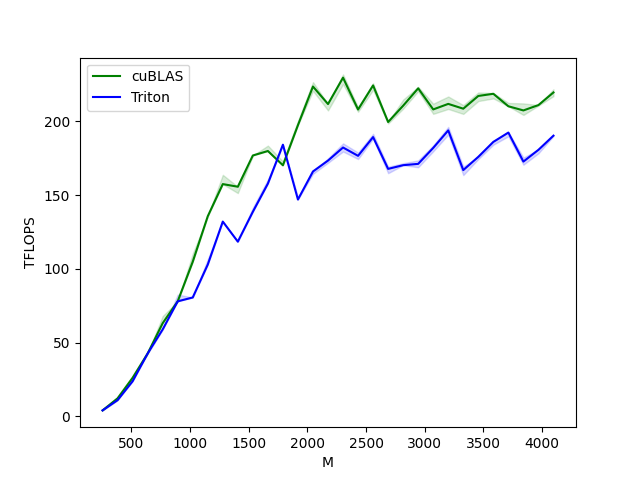
现在我们可以将我们的内核性能与cuBLAS或rocBLAS进行比较。这里我们主要关注方阵,但您可以自由调整此脚本以基准测试任何其他矩阵形状。
ref_lib = 'cuBLAS' if is_cuda() else 'rocBLAS'
configs = []
for fp8_inputs in [False, True]:
if fp8_inputs and (not TORCH_HAS_FP8 or not is_cuda()):
continue
configs.append(
triton.testing.Benchmark(
x_names=["M", "N", "K"], # Argument names to use as an x-axis for the plot
x_vals=[128 * i for i in range(2, 33)], # Different possible values for `x_name`
line_arg="provider", # Argument name whose value corresponds to a different line in the plot
# Possible values for `line_arg`
# Don't compare to cublas for fp8 cases as torch.matmul doesn't support fp8 at the moment.
line_vals=["triton"] if fp8_inputs else [ref_lib.lower(), "triton"], # Label name for the lines
line_names=["Triton"] if fp8_inputs else [ref_lib, "Triton"], # Line styles
styles=[("green", "-"), ("blue", "-")],
ylabel="TFLOPS", # Label name for the y-axis
plot_name="matmul-performance-" +
("fp16" if not fp8_inputs else "fp8"), # Name for the plot, used also as a file name for saving the plot.
args={"fp8_inputs": fp8_inputs},
))
@triton.testing.perf_report(configs)
def benchmark(M, N, K, provider, fp8_inputs):
a = torch.randn((M, K), device=DEVICE, dtype=torch.float16)
b = torch.randn((K, N), device=DEVICE, dtype=torch.float16)
if TORCH_HAS_FP8 and fp8_inputs:
a = a.to(torch.float8_e5m2)
b = b.T
b = b.to(torch.float8_e5m2)
quantiles = [0.5, 0.2, 0.8]
if provider == ref_lib.lower():
ms, min_ms, max_ms = triton.testing.do_bench(lambda: torch.matmul(a, b), quantiles=quantiles)
if provider == 'triton':
ms, min_ms, max_ms = triton.testing.do_bench(lambda: matmul(a, b), quantiles=quantiles)
perf = lambda ms: 2 * M * N * K * 1e-12 / (ms * 1e-3)
return perf(ms), perf(max_ms), perf(min_ms)
benchmark.run(show_plots=True, print_data=True)
matmul-performance-fp16:
M N K cuBLAS Triton
0 256.0 256.0 256.0 4.096000 4.096000
1 384.0 384.0 384.0 12.288000 11.059200
2 512.0 512.0 512.0 26.214401 23.831273
3 640.0 640.0 640.0 42.666665 42.666665
4 768.0 768.0 768.0 63.195428 58.982401
5 896.0 896.0 896.0 78.051553 78.051553
6 1024.0 1024.0 1024.0 104.857603 80.659693
7 1152.0 1152.0 1152.0 135.726544 102.964963
8 1280.0 1280.0 1280.0 157.538463 132.129034
9 1408.0 1408.0 1408.0 155.765024 118.516867
10 1536.0 1536.0 1536.0 176.947204 138.782120
11 1664.0 1664.0 1664.0 179.978245 157.875646
12 1792.0 1792.0 1792.0 170.294302 184.252856
13 1920.0 1920.0 1920.0 197.485709 147.063826
14 2048.0 2048.0 2048.0 223.696203 166.111053
15 2176.0 2176.0 2176.0 211.827867 173.479720
16 2304.0 2304.0 2304.0 229.691080 182.350177
17 2432.0 2432.0 2432.0 208.107149 176.694739
18 2560.0 2560.0 2560.0 224.438347 189.410412
19 2688.0 2688.0 2688.0 199.647657 167.845378
20 2816.0 2816.0 2816.0 210.696652 170.368000
21 2944.0 2944.0 2944.0 222.482283 171.257840
22 3072.0 3072.0 3072.0 208.173173 182.067852
23 3200.0 3200.0 3200.0 211.920530 193.939388
24 3328.0 3328.0 3328.0 208.670419 167.033172
25 3456.0 3456.0 3456.0 217.308808 176.029626
26 3584.0 3584.0 3584.0 218.772251 186.160228
27 3712.0 3712.0 3712.0 210.310194 192.480434
28 3840.0 3840.0 3840.0 207.489687 172.800004
29 3968.0 3968.0 3968.0 211.114084 180.776197
30 4096.0 4096.0 4096.0 219.668951 190.379752
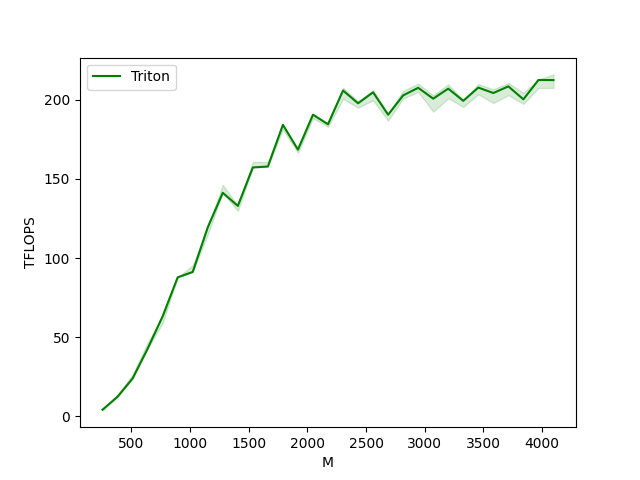
matmul-performance-fp8:
M N K Triton
0 256.0 256.0 256.0 4.096000
1 384.0 384.0 384.0 12.288000
2 512.0 512.0 512.0 23.831273
3 640.0 640.0 640.0 42.666665
4 768.0 768.0 768.0 63.195428
5 896.0 896.0 896.0 87.808000
6 1024.0 1024.0 1024.0 91.180520
7 1152.0 1152.0 1152.0 119.439363
8 1280.0 1280.0 1280.0 141.241376
9 1408.0 1408.0 1408.0 132.970149
10 1536.0 1536.0 1536.0 157.286398
11 1664.0 1664.0 1664.0 157.875646
12 1792.0 1792.0 1792.0 184.252856
13 1920.0 1920.0 1920.0 168.585369
14 2048.0 2048.0 2048.0 190.650180
15 2176.0 2176.0 2176.0 184.620623
16 2304.0 2304.0 2304.0 205.929926
17 2432.0 2432.0 2432.0 197.848332
18 2560.0 2560.0 2560.0 204.800005
19 2688.0 2688.0 2688.0 190.618370
20 2816.0 2816.0 2816.0 202.856788
21 2944.0 2944.0 2944.0 207.650139
22 3072.0 3072.0 3072.0 200.791153
23 3200.0 3200.0 3200.0 207.119744
24 3328.0 3328.0 3328.0 199.421865
25 3456.0 3456.0 3456.0 207.787554
26 3584.0 3584.0 3584.0 204.353162
27 3712.0 3712.0 3712.0 208.553950
28 3840.0 3840.0 3840.0 200.347822
29 3968.0 3968.0 3968.0 212.585252
30 4096.0 4096.0 4096.0 212.537978
脚本总运行时间:(2分9.932秒)