注意
跳至末尾 下载完整示例代码。
层归一化¶
在本教程中，您将编写一个高性能的层归一化内核，其运行速度比PyTorch实现更快。
在此过程中，您将了解：
在Triton中实现反向传播。
在Triton中实现并行归约。
动机¶
LayerNorm 算子最初在 [BA2016] 中提出，旨在提升序列模型（如Transformers）或小批量神经网络的性能。 它接收向量 \(x\) 作为输入，并输出相同形状的向量 \(y\)。 归一化过程通过减去均值并除以 \(x\) 的标准差来实现。 归一化后，会应用一个带有权重 \(w\) 和偏置 \(b\) 的可学习线性变换。 前向传播过程可以表示为：
\[y = \frac{ x - \text{E}[x] }{ \sqrt{\text{Var}(x) + \epsilon} } * w + b\]
其中\(\epsilon\)是添加到分母的一个小常数，用于数值稳定性。 让我们首先看一下前向传播的实现。
import torch
import triton
import triton.language as tl
try:
# This is https://github.com/NVIDIA/apex, NOT the apex on PyPi, so it
# should not be added to extras_require in setup.py.
import apex
HAS_APEX = True
except ModuleNotFoundError:
HAS_APEX = False
DEVICE = triton.runtime.driver.active.get_active_torch_device()
@triton.jit
def _layer_norm_fwd_fused(
X, # pointer to the input
Y, # pointer to the output
W, # pointer to the weights
B, # pointer to the biases
Mean, # pointer to the mean
Rstd, # pointer to the 1/std
stride, # how much to increase the pointer when moving by 1 row
N, # number of columns in X
eps, # epsilon to avoid division by zero
BLOCK_SIZE: tl.constexpr,
):
# Map the program id to the row of X and Y it should compute.
row = tl.program_id(0)
Y += row * stride
X += row * stride
# Compute mean
mean = 0
_mean = tl.zeros([BLOCK_SIZE], dtype=tl.float32)
for off in range(0, N, BLOCK_SIZE):
cols = off + tl.arange(0, BLOCK_SIZE)
a = tl.load(X + cols, mask=cols < N, other=0.).to(tl.float32)
_mean += a
mean = tl.sum(_mean, axis=0) / N
# Compute variance
_var = tl.zeros([BLOCK_SIZE], dtype=tl.float32)
for off in range(0, N, BLOCK_SIZE):
cols = off + tl.arange(0, BLOCK_SIZE)
x = tl.load(X + cols, mask=cols < N, other=0.).to(tl.float32)
x = tl.where(cols < N, x - mean, 0.)
_var += x * x
var = tl.sum(_var, axis=0) / N
rstd = 1 / tl.sqrt(var + eps)
# Write mean / rstd
tl.store(Mean + row, mean)
tl.store(Rstd + row, rstd)
# Normalize and apply linear transformation
for off in range(0, N, BLOCK_SIZE):
cols = off + tl.arange(0, BLOCK_SIZE)
mask = cols < N
w = tl.load(W + cols, mask=mask)
b = tl.load(B + cols, mask=mask)
x = tl.load(X + cols, mask=mask, other=0.).to(tl.float32)
x_hat = (x - mean) * rstd
y = x_hat * w + b
# Write output
tl.store(Y + cols, y, mask=mask)
反向传播¶
层归一化算子的反向传播比前向传播稍微复杂一些。 设\(\hat{x}\)为线性变换前的归一化输入\(\frac{ x - \text{E}[x] }{ \sqrt{\text{Var}(x) + \epsilon} }\)， 关于\(x\)的向量-雅可比积(VJP)\(\nabla_{x}\)由下式给出：
\[\nabla_{x} = \frac{1}{\sigma}\Big( \nabla_{y} \odot w - \underbrace{ \big( \frac{1}{N} \hat{x} \cdot (\nabla_{y} \odot w) \big) }_{c_1} \odot \hat{x} - \underbrace{ \frac{1}{N} \nabla_{y} \cdot w }_{c_2} \Big)\]
其中 \(\odot\) 表示逐元素乘法，\(\cdot\) 表示点积，\(\sigma\) 是标准差。 \(c_1\) 和 \(c_2\) 是中间常量，用于提高后续实现的可读性。
对于权重 \(w\) 和偏置 \(b\)，VJPs \(\nabla_{w}\) 和 \(\nabla_{b}\) 更为直接：
\[\nabla_{w} = \nabla_{y} \odot \hat{x} \quad \text{and} \quad \nabla_{b} = \nabla_{y}\]
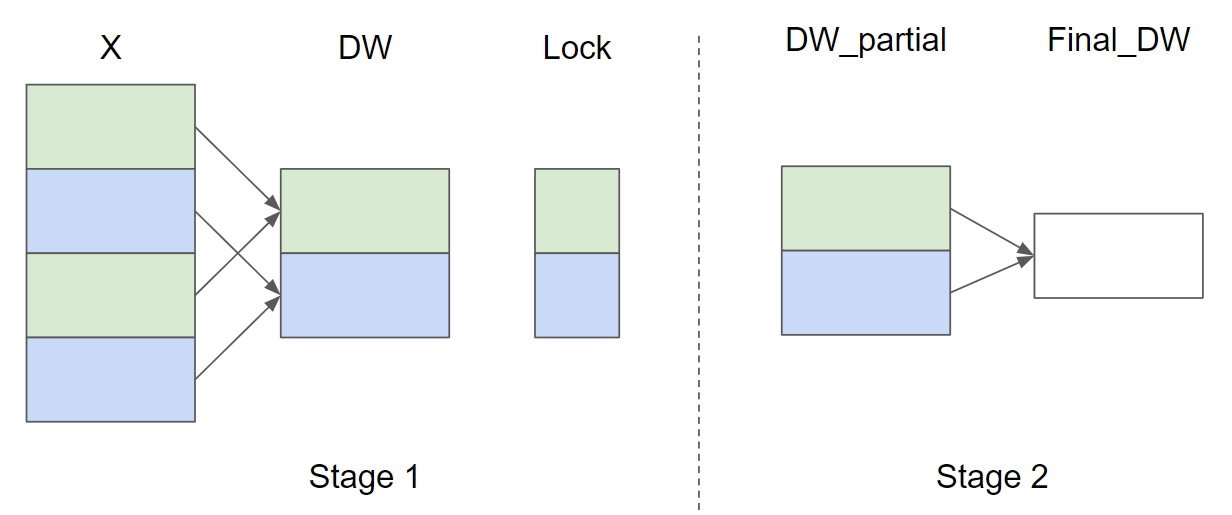
由于同一批次中的所有行都使用相同的权重\(w\)和偏置\(b\)，它们的梯度需要进行求和。 为了高效执行这一步骤，我们采用并行归约策略：每个内核实例将部分\(\nabla_{w}\)和\(\nabla_{b}\)跨特定行累加到\(\text{GROUP_SIZE_M}\)个独立缓冲区之一中。 这些缓冲区保留在L2缓存中，然后由另一个函数进一步归约以计算实际的\(\nabla_{w}\)和\(\nabla_{b}\)。
设输入行数 \(M = 4\) 且 \(\text{GROUP_SIZE_M} = 2\)， 以下是 \(\nabla_{w}\) 的并行归约策略示意图（为简洁起见省略了 \(\nabla_{b}\)）：
在阶段1中，X矩阵中相同颜色的行共享同一个缓冲区，因此使用锁来确保每次只有一个内核实例写入缓冲区。
在阶段2中，这些缓冲区会进一步归约以计算最终的\(\nabla_{w}\)和\(\nabla_{b}\)。
在以下实现中，阶段1由函数_layer_norm_bwd_dx_fused实现，阶段2由函数_layer_norm_bwd_dwdb实现。
@triton.jit
def _layer_norm_bwd_dx_fused(DX, # pointer to the input gradient
DY, # pointer to the output gradient
DW, # pointer to the partial sum of weights gradient
DB, # pointer to the partial sum of biases gradient
X, # pointer to the input
W, # pointer to the weights
Mean, # pointer to the mean
Rstd, # pointer to the 1/std
Lock, # pointer to the lock
stride, # how much to increase the pointer when moving by 1 row
N, # number of columns in X
GROUP_SIZE_M: tl.constexpr, BLOCK_SIZE_N: tl.constexpr):
# Map the program id to the elements of X, DX, and DY it should compute.
row = tl.program_id(0)
cols = tl.arange(0, BLOCK_SIZE_N)
mask = cols < N
X += row * stride
DY += row * stride
DX += row * stride
# Offset locks and weights/biases gradient pointer for parallel reduction
lock_id = row % GROUP_SIZE_M
Lock += lock_id
Count = Lock + GROUP_SIZE_M
DW = DW + lock_id * N + cols
DB = DB + lock_id * N + cols
# Load data to SRAM
x = tl.load(X + cols, mask=mask, other=0).to(tl.float32)
dy = tl.load(DY + cols, mask=mask, other=0).to(tl.float32)
w = tl.load(W + cols, mask=mask).to(tl.float32)
mean = tl.load(Mean + row)
rstd = tl.load(Rstd + row)
# Compute dx
xhat = (x - mean) * rstd
wdy = w * dy
xhat = tl.where(mask, xhat, 0.)
wdy = tl.where(mask, wdy, 0.)
c1 = tl.sum(xhat * wdy, axis=0) / N
c2 = tl.sum(wdy, axis=0) / N
dx = (wdy - (xhat * c1 + c2)) * rstd
# Write dx
tl.store(DX + cols, dx, mask=mask)
# Accumulate partial sums for dw/db
partial_dw = (dy * xhat).to(w.dtype)
partial_db = (dy).to(w.dtype)
while tl.atomic_cas(Lock, 0, 1) == 1:
pass
count = tl.load(Count)
# First store doesn't accumulate
if count == 0:
tl.atomic_xchg(Count, 1)
else:
partial_dw += tl.load(DW, mask=mask)
partial_db += tl.load(DB, mask=mask)
tl.store(DW, partial_dw, mask=mask)
tl.store(DB, partial_db, mask=mask)
# need a barrier to ensure all threads finished before
# releasing the lock
tl.debug_barrier()
# Release the lock
tl.atomic_xchg(Lock, 0)
@triton.jit
def _layer_norm_bwd_dwdb(DW, # pointer to the partial sum of weights gradient
DB, # pointer to the partial sum of biases gradient
FINAL_DW, # pointer to the weights gradient
FINAL_DB, # pointer to the biases gradient
M, # GROUP_SIZE_M
N, # number of columns
BLOCK_SIZE_M: tl.constexpr, BLOCK_SIZE_N: tl.constexpr):
# Map the program id to the elements of DW and DB it should compute.
pid = tl.program_id(0)
cols = pid * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)
dw = tl.zeros((BLOCK_SIZE_M, BLOCK_SIZE_N), dtype=tl.float32)
db = tl.zeros((BLOCK_SIZE_M, BLOCK_SIZE_N), dtype=tl.float32)
# Iterate through the rows of DW and DB to sum the partial sums.
for i in range(0, M, BLOCK_SIZE_M):
rows = i + tl.arange(0, BLOCK_SIZE_M)
mask = (rows[:, None] < M) & (cols[None, :] < N)
offs = rows[:, None] * N + cols[None, :]
dw += tl.load(DW + offs, mask=mask, other=0.)
db += tl.load(DB + offs, mask=mask, other=0.)
# Write the final sum to the output.
sum_dw = tl.sum(dw, axis=0)
sum_db = tl.sum(db, axis=0)
tl.store(FINAL_DW + cols, sum_dw, mask=cols < N)
tl.store(FINAL_DB + cols, sum_db, mask=cols < N)
基准测试¶
我们现在可以将我们的内核性能与PyTorch进行比较。这里我们重点关注每个特征小于64KB的输入。具体来说，可以设置'mode': 'backward'来对反向传播进行基准测试。
class LayerNorm(torch.autograd.Function):
@staticmethod
def forward(ctx, x, normalized_shape, weight, bias, eps):
# allocate output
y = torch.empty_like(x)
# reshape input data into 2D tensor
x_arg = x.reshape(-1, x.shape[-1])
M, N = x_arg.shape
mean = torch.empty((M, ), dtype=torch.float32, device=x.device)
rstd = torch.empty((M, ), dtype=torch.float32, device=x.device)
# Less than 64KB per feature: enqueue fused kernel
MAX_FUSED_SIZE = 65536 // x.element_size()
BLOCK_SIZE = min(MAX_FUSED_SIZE, triton.next_power_of_2(N))
if N > BLOCK_SIZE:
raise RuntimeError("This layer norm doesn't support feature dim >= 64KB.")
# heuristics for number of warps
num_warps = min(max(BLOCK_SIZE // 256, 1), 8)
# enqueue kernel
_layer_norm_fwd_fused[(M, )]( #
x_arg, y, weight, bias, mean, rstd, #
x_arg.stride(0), N, eps, #
BLOCK_SIZE=BLOCK_SIZE, num_warps=num_warps, num_ctas=1)
ctx.save_for_backward(x, weight, bias, mean, rstd)
ctx.BLOCK_SIZE = BLOCK_SIZE
ctx.num_warps = num_warps
ctx.eps = eps
return y
@staticmethod
def backward(ctx, dy):
x, w, b, m, v = ctx.saved_tensors
# heuristics for amount of parallel reduction stream for DW/DB
N = w.shape[0]
GROUP_SIZE_M = 64
if N <= 8192: GROUP_SIZE_M = 96
if N <= 4096: GROUP_SIZE_M = 128
if N <= 1024: GROUP_SIZE_M = 256
# allocate output
locks = torch.zeros(2 * GROUP_SIZE_M, dtype=torch.int32, device=w.device)
_dw = torch.zeros((GROUP_SIZE_M, N), dtype=x.dtype, device=w.device)
_db = torch.zeros((GROUP_SIZE_M, N), dtype=x.dtype, device=w.device)
dw = torch.empty((N, ), dtype=w.dtype, device=w.device)
db = torch.empty((N, ), dtype=w.dtype, device=w.device)
dx = torch.empty_like(dy)
# enqueue kernel using forward pass heuristics
# also compute partial sums for DW and DB
x_arg = x.reshape(-1, x.shape[-1])
M, N = x_arg.shape
_layer_norm_bwd_dx_fused[(M, )]( #
dx, dy, _dw, _db, x, w, m, v, locks, #
x_arg.stride(0), N, #
BLOCK_SIZE_N=ctx.BLOCK_SIZE, #
GROUP_SIZE_M=GROUP_SIZE_M, #
num_warps=ctx.num_warps)
grid = lambda meta: (triton.cdiv(N, meta['BLOCK_SIZE_N']), )
# accumulate partial sums in separate kernel
_layer_norm_bwd_dwdb[grid](
_dw, _db, dw, db, min(GROUP_SIZE_M, M), N, #
BLOCK_SIZE_M=32, #
BLOCK_SIZE_N=128, num_ctas=1)
return dx, None, dw, db, None
layer_norm = LayerNorm.apply
def test_layer_norm(M, N, dtype, eps=1e-5, device=DEVICE):
# create data
x_shape = (M, N)
w_shape = (x_shape[-1], )
weight = torch.rand(w_shape, dtype=dtype, device=device, requires_grad=True)
bias = torch.rand(w_shape, dtype=dtype, device=device, requires_grad=True)
x = -2.3 + 0.5 * torch.randn(x_shape, dtype=dtype, device=device)
dy = .1 * torch.randn_like(x)
x.requires_grad_(True)
# forward pass
y_tri = layer_norm(x, w_shape, weight, bias, eps)
y_ref = torch.nn.functional.layer_norm(x, w_shape, weight, bias, eps).to(dtype)
# backward pass (triton)
y_tri.backward(dy, retain_graph=True)
dx_tri, dw_tri, db_tri = [_.grad.clone() for _ in [x, weight, bias]]
x.grad, weight.grad, bias.grad = None, None, None
# backward pass (torch)
y_ref.backward(dy, retain_graph=True)
dx_ref, dw_ref, db_ref = [_.grad.clone() for _ in [x, weight, bias]]
# compare
assert torch.allclose(y_tri, y_ref, atol=1e-2, rtol=0)
assert torch.allclose(dx_tri, dx_ref, atol=1e-2, rtol=0)
assert torch.allclose(db_tri, db_ref, atol=1e-2, rtol=0)
assert torch.allclose(dw_tri, dw_ref, atol=1e-2, rtol=0)
@triton.testing.perf_report(
triton.testing.Benchmark(
x_names=['N'],
x_vals=[512 * i for i in range(2, 32)],
line_arg='provider',
line_vals=['triton', 'torch'] + (['apex'] if HAS_APEX else []),
line_names=['Triton', 'Torch'] + (['Apex'] if HAS_APEX else []),
styles=[('blue', '-'), ('green', '-'), ('orange', '-')],
ylabel='GB/s',
plot_name='layer-norm-backward',
args={'M': 4096, 'dtype': torch.float16, 'mode': 'backward'},
))
def bench_layer_norm(M, N, dtype, provider, mode='backward', eps=1e-5, device=DEVICE):
# create data
x_shape = (M, N)
w_shape = (x_shape[-1], )
weight = torch.rand(w_shape, dtype=dtype, device=device, requires_grad=True)
bias = torch.rand(w_shape, dtype=dtype, device=device, requires_grad=True)
x = -2.3 + 0.5 * torch.randn(x_shape, dtype=dtype, device=device)
dy = .1 * torch.randn_like(x)
x.requires_grad_(True)
quantiles = [0.5, 0.2, 0.8]
def y_fwd():
if provider == "triton":
return layer_norm(x, w_shape, weight, bias, eps) # noqa: F811, E704
if provider == "torch":
return torch.nn.functional.layer_norm(x, w_shape, weight, bias, eps) # noqa: F811, E704
if provider == "apex":
apex_layer_norm = (apex.normalization.FusedLayerNorm(w_shape).to(x.device).to(x.dtype))
return apex_layer_norm(x) # noqa: F811, E704
# forward pass
if mode == 'forward':
gbps = lambda ms: 2 * x.numel() * x.element_size() * 1e-9 / (ms * 1e-3)
ms, min_ms, max_ms = triton.testing.do_bench(y_fwd, quantiles=quantiles, rep=500)
# backward pass
if mode == 'backward':
y = y_fwd()
gbps = lambda ms: 3 * x.numel() * x.element_size() * 1e-9 / (ms * 1e-3) # noqa: F811, E704
ms, min_ms, max_ms = triton.testing.do_bench(lambda: y.backward(dy, retain_graph=True), quantiles=quantiles,
grad_to_none=[x], rep=500)
return gbps(ms), gbps(max_ms), gbps(min_ms)
test_layer_norm(1151, 8192, torch.float16)
bench_layer_norm.run(save_path='.', print_data=True)
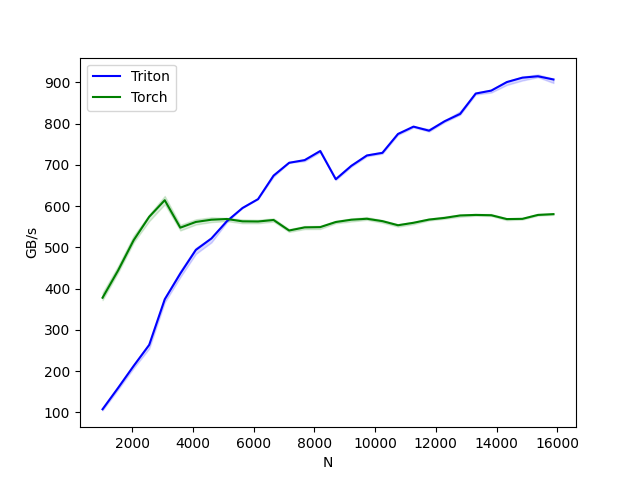
layer-norm-backward:
N Triton Torch
0 1024.0 107.789472 378.092307
1 1536.0 159.584417 444.144584
2 2048.0 212.779222 517.389457
3 2560.0 263.690988 574.205608
4 3072.0 374.253805 614.400016
5 3584.0 436.629439 547.872604
6 4096.0 493.989945 561.737163
7 4608.0 521.660380 567.138460
8 5120.0 563.669722 568.888888
9 5632.0 595.453753 563.200014
10 6144.0 616.970709 562.809189
11 6656.0 674.025316 566.468098
12 7168.0 705.049194 540.981122
13 7680.0 711.660251 548.571433
14 8192.0 733.611931 549.184373
15 8704.0 665.273876 561.548373
16 9216.0 697.741329 567.138460
17 9728.0 722.823562 569.443892
18 10240.0 729.258150 563.669722
19 10752.0 774.918911 553.751076
20 11264.0 792.774179 559.701851
21 11776.0 782.891938 567.518063
22 12288.0 805.770507 571.534916
23 12800.0 823.592520 577.443635
24 13312.0 872.918050 578.782596
25 13824.0 880.042465 578.006963
26 14336.0 900.691103 568.700819
27 14848.0 911.386169 569.252402
28 15360.0 914.739425 578.712698
29 15872.0 906.971436 580.682936
参考文献¶
[BA2016]
Jimmy Lei Ba 和 Jamie Ryan Kiros 以及 Geoffrey E. Hinton，《层归一化》，Arxiv 2016
脚本总运行时间： (0 分钟 28.959 秒)