损失函数

PyKEEN中集成的损失函数。

我们没有选择重用PyTorch中的内置损失函数，而是决定重新实现pytorch.nn.modules.loss中的一些代码，以便在类层次结构中编码PyKEEN接受的三种不同链接的损失函数。这使得PyKEEN能够更动态地处理不同类型的损失函数并共享代码。此外，它还为潜在用户提供了更多的见解。

在以下对点损失函数、对损失函数和集损失函数的解释中，我们将假设实体集\(\mathcal{E}\)、关系集\(\mathcal{R}\)、可能的三元组集\(\mathcal{T} = \mathcal{E} \times \mathcal{R} \times \mathcal{E}\)、可能三元组的可能子集\(2^{\mathcal{T}}\)（即\(\mathcal{T}\)的幂集）、正三元组集\(\mathcal{K}\)、负三元组集\(\mathcal{\bar{K}}\)、评分函数（例如TransE）\(f: \mathcal{T} \rightarrow \mathbb{R}\)和标签函数\(l:\mathcal{T} \rightarrow \{0,1\}\)，其中值为1表示三元组为正（即\((h,r,t) \in \mathcal{K}\)），值为0表示三元组为负（即\((h,r,t) \notin \mathcal{K}\)）。

注意

在大多数实际的知识图谱嵌入模型使用案例中，您将观察到正三元组的一个子集 \(\mathcal{T_{obs}} \subset \mathcal{K}\)，而没有观察到负三元组。根据训练假设（sLCWA 或 LCWA），这意味着负三元组将以各种模式生成。

注意

遵循开放世界假设（OWA），三元组 \(\mathcal{\bar{K}}\) 更适合被称为“非正”而非负。这对于逐点损失函数最为相关。对于成对和集合损失函数，三元组被比较为更/较正，二元分类不相关。

逐点损失函数

点损失应用于单个三元组。它的形式为\(L: \mathcal{T} \rightarrow \mathbb{R}\)，并根据其标签计算三元组的实数值。通常，点损失函数的形式为\(g: \mathbb{R} \times \{0,1\} \rightarrow \mathbb{R}\)，基于评分函数和标签函数。

\[L(k) = g(f(k), l(k))\]

示例

逐点损失	公式
平方误差	\(g(s, l) = \frac{1}{2}(s - l)^2\)
二元交叉熵	\(g(s, l) = -(l*\log (\sigma(s))+(1-l)*(\log (1-\sigma(s))))\)
逐点铰链	\(g(s, l) = \max(0, \lambda -\hat{l}*s)\)
软点向铰链	\(g(s, l) = \log(1+\exp(\lambda-\hat{l}*s))\)
逐点逻辑（softplus）	\(g(s, l) = \log(1+\exp(-\hat{l}*s))\)

对于逐点逻辑损失和逐点铰链损失，\(\hat{l}\) 已经从 \(\{0,1\}\) 重新缩放到 \(\{-1,1\}\)。 Sigmoid逻辑损失函数定义为 \(\sigma(z) = \frac{1}{1 + e^{-z}}\)。

注意

逐点逻辑损失可以被视为逐点软铰链损失的一个特例，其中 \(\lambda = 0\)。

批处理

一组三元组（即一个批次）的点损失 \(\mathcal{L}_L: 2^{\mathcal{T}} \rightarrow \mathbb{R}\) 被定义为子集 \(\mathcal{B} \in 2^{\mathcal{T}}\) 中每个三元组的点损失的算术平均值：

\[\mathcal{L}_L(\mathcal{B}) = \frac{1}{|\mathcal{B}|} \sum \limits_{k \in \mathcal{B}} L(k)\]

成对损失函数

成对损失应用于一对三元组 - 一个正例和一个负例。它被定义为 \(L: \mathcal{K} \times \mathcal{\bar{K}} \rightarrow \mathbb{R}\) 并为这对三元组计算一个实数值。

PyKEEN中实现的所有损失函数都会根据所选的交互函数\(L{*}: \mathbb{R} \times \mathbb{R} \rightarrow \mathbb{R}\)诱导出一个辅助损失函数，该函数只是将分数传递过去。请注意，\(L\)经常与\(L^{*}\)互换使用。

\[L(k, \bar{k}) = L^{*}(f(k), f(\bar{k}))\]

Delta 成对损失函数

Delta成对损失是根据负三元组和正三元组得分之间的差异计算的（例如，\(\Delta := f(\bar{k}) - f(k)\)），使用转移函数\(g: \mathbb{R} \rightarrow \mathbb{R}\)，其形式为：

\[L^{*}(f(k), f(\bar{k})) = g(f(\bar{k}) - f(k)) := g(\Delta)\]

下表显示了成对损失函数的差异：

成对损失	激活	边距	公式
成对铰链（边际排序）	ReLU	\(\lambda \neq 0\)	\(g(\Delta) = \max(0, \Delta + \lambda)\)
软成对铰链（软间隔排序）	softplus	\(\lambda \neq 0\)	\(g(\Delta) = \log(1 + \exp(\Delta + \lambda))\)
成对逻辑回归	softplus	\(\lambda=0\)	\(g(\Delta) = \log(1 + \exp(\Delta))\)

注意

成对逻辑损失可以被视为成对软铰链损失的一个特例，其中\(\lambda = 0\)。

不可分割的成对损失函数

以下成对损失函数使用\(L(k, \bar{k}) = \dots\)的完整广义形式来定义：

成对损失	公式
双重损失	\(h(\bar{\lambda} + f(\bar{k})) + h(\lambda - f(k))\)

批处理

一组正/负三元组对的成对损失 \(\mathcal{L}_L: 2^{\mathcal{K} \times \mathcal{\bar{K}}} \rightarrow \mathbb{R}\) 被定义为子集 \(\mathcal{B} \in 2^{\mathcal{K} \times \mathcal{\bar{K}}}\) 中每对正负三元组的成对损失的算术平均值。

\[\mathcal{L}_L(\mathcal{B}) = \frac{1}{|\mathcal{B}|} \sum \limits_{(k, \bar{k}) \in \mathcal{B}} L(k, \bar{k})\]

集合损失函数

集合损失应用于一组可以是正或负的三元组。它被定义为 \(L: 2^{\mathcal{T}} \rightarrow \mathbb{R}\)。在PyKEEN中实现的两个集合损失函数， pykeen.losses.NSSALoss 和 pykeen.losses.CrossEntropyLoss 在它们的范式上有很大的不同， 但都共享三元组不严格为正或负的概念。

\[L(k_1, ... k_n) = g(f(k_1), ..., f(k_n))\]

批处理

对于一组三元组集合的三元组 \(\mathcal{L}_L: 2^{2^{\mathcal{T}}} \rightarrow \mathbb{R}\) 的成对损失被定义为子集 \(\mathcal{B} \in 2^{2^{\mathcal{T}}}\) 中每个三元组集合 \(\mathcal{b}\) 的集合损失的算术平均值。

\[\mathcal{L}_L(\mathcal{B}) = \frac{1}{|\mathcal{B}|} \sum \limits_{\mathcal{b} \in \mathcal{B}} L(\mathcal{b})\]

类

PointwiseLoss([reduction])	逐点损失函数为每个三元组标签对计算一个独立的损失项。
DeltaPointwiseLoss([margin, ...])	用于逐点差异损失的通用类。
MarginPairwiseLoss([margin, ...])	广义边际排序损失。
PairwiseLoss([reduction])	成对损失函数比较正三元组和负三元组的分数。
SetwiseLoss([reduction])	集合损失函数比较了几个三元组的分数。
AdversarialLoss([...])	一种带有对抗性负样本加权的损失。
AdversarialBCEWithLogitsLoss([...])	一个对抗性加权的BCE损失。
BCEAfterSigmoidLoss([reduction])	数值不稳定的显式Sigmoid + BCE损失版本。
BCEWithLogitsLoss([reduction])	二元交叉熵损失。
CrossEntropyLoss([reduction])	评估softmax输出后的交叉熵的交叉熵损失。
FocalLoss(*[, gamma, alpha])	由[lin2018]提出的焦点损失。
InfoNCELoss([margin, ...])	由[wang2022]提出的带有附加边际的InfoNCE损失。
MarginRankingLoss([margin, reduction])	成对铰链损失（即边际排序损失）。
MSELoss([reduction])	均方误差损失。
NSSALoss([margin, adversarial_temperature, ...])	由[sun2019]提出的自对抗负采样损失函数。
SoftplusLoss([reduction])	逐点逻辑损失（即softplus损失）。
SoftPointwiseHingeLoss([margin, reduction])	软点对点铰链损失。
PointwiseHingeLoss([margin, reduction])	逐点铰链损失。
DoubleMarginLoss(*[, positive_margin, ...])	基于限制的评分损失，具有来自[sun2018]的正负元素的单独边界。
SoftMarginRankingLoss([margin, reduction])	软成对铰链损失（即软边际排序损失）。
PairwiseLogisticLoss([reduction])	成对逻辑损失。

变量

loss_resolver

损失模块的解析器

类继承图

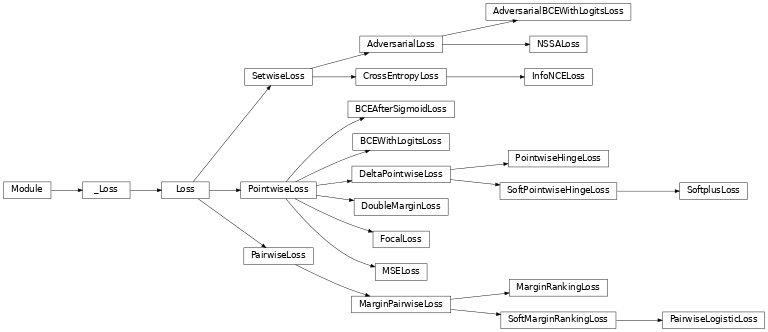
基础类

class Loss(reduction: str = 'mean')

一个损失函数。

初始化损失。

Parameters:

reduction (str) – 减少方式，参见 pykeen.nn.modules._Loss

hpo_default: ClassVar[Mapping[str, Any]] = {}

优化损失超参数的默认策略

process_lcwa_scores(predictions: Tensor, labels: Tensor, label_smoothing: float | None = None, num_entities: int | None = None) → Tensor

处理来自LCWA训练循环的分数。

Parameters:

• predictions (Tensor) – 形状: (batch_size, num_entities) 分数。

• labels (Tensor) – 形状: (batch_size, num_entities) 标签。

• label_smoothing (float | None) – 一个可选的标签平滑参数。

• num_entities (int | None) – 实体数量（用于标签平滑的必需参数）。

Returns:

一个标量损失值。

Return type:

Tensor

process_slcwa_scores(positive_scores: Tensor, negative_scores: Tensor, label_smoothing: float | None = None, batch_filter: Tensor | None = None, num_entities: int | None = None) → Tensor

处理来自sLCWA训练循环的分数。

Parameters:

• positive_scores (Tensor) – 形状: (batch_size, 1) 正三元组的分数。

• negative_scores (Tensor) – 形状: (batch_size, num_neg_per_pos) 或 (num_unfiltered_negatives,) 负三元组的分数，可以是密集的2D形状，或者如果它们已经被过滤，可以是稀疏形状。如果它们以稀疏形状给出，还需要提供batch_filter。

• label_smoothing (float | None) – 一个可选的标签平滑参数。

• batch_filter (Tensor | None) – 形状: (batch_size, num_neg_per_pos) 一个可选的负分数过滤器，用于保留哪些负分数。仅在负分数已被预过滤时提供。

• num_entities (int | None) – 实体的数量。仅在启用标签平滑时需要。

Returns:

一个标量损失项。

Return type:

Tensor

synonyms: ClassVar[set[str] | None] = None

这个损失的近义词