训练

使用多模态信息的KGE模型训练循环。

在以下训练循环的解释中，我们将假设实体集 \(\mathcal{E}\)，关系集 \(\mathcal{R}\)，可能的三元组集 \(\mathcal{T} = \mathcal{E} \times \mathcal{R} \times \mathcal{E}\)。我们将 \(\mathcal{T}\) 分层为 不相交并集 的正三元组 \(\mathcal{T^{+}} \subseteq \mathcal{T}\) 和负三元组 \(\mathcal{T^{-}} \subseteq \mathcal{T}\)，使得 \(\mathcal{T^{+}} \cap \mathcal{T^{-}} = \emptyset\) 且 \(\mathcal{T^{+}} \cup \mathcal{T^{-}} = \mathcal{T}\)。

在开放世界假设下构建的知识图谱 \(\mathcal{K}\) 包含所有可能正三元组的一个子集，使得 \(\mathcal{K} \subseteq \mathcal{T^{+}}\)。

假设

开放世界假设

在开放世界假设（OWA）下进行训练时，所有不属于知识图谱的三元组都被认为是未知的（例如，既不是正例也不是负例）。这会导致欠拟合（即过度泛化），因此通常不适合用于训练知识图谱嵌入模型[nickel2016review]。PyKEEN 不 实现使用OWA的训练循环。

警告

许多出版物和软件包错误地使用OWA来指代随机局部封闭世界假设（sLCWA）。请参阅以下解释。

封闭世界假设

在封闭世界假设（CWA）下进行训练时，所有不属于知识图谱的三元组都被视为负样本。由于大多数知识图谱本质上是不完整的，这会导致过拟合，因此通常不适合用于训练知识图谱嵌入模型。PyKEEN 不 实现使用CWA的训练循环。

局部封闭世界假设

在本地封闭世界假设（LCWA；在[dong2014]中引入）下进行训练时，知识图谱中不包含的特定三元组子集被视为负面样本。

策略	本地生成器	全局生成器
头部	\(\mathcal{T}_h^-(r,t)=\{(h,r,t) \mid h \in \mathcal{E} \land (h,r,t) \notin \mathcal{K} \}\)	\(\bigcup\limits_{(\_,r,t) \in \mathcal{K}} \mathcal{T}_h^-(r,t)\)
关系	\(\mathcal{T}_r^-(h,t)=\{(h,r,t) \mid r \in \mathcal{R} \land (h,r,t) \notin \mathcal{K} \}\)	\(\bigcup\limits_{(h,\_,t) \in \mathcal{K}} \mathcal{T}_r^-(h,t)\)
尾部	\(\mathcal{T}_t^-(h,r)=\{(h,r,t) \mid t \in \mathcal{E} \land (h,r,t) \notin \mathcal{K} \}\)	\(\bigcup\limits_{(h,r,\_) \in \mathcal{K}} \mathcal{T}_t^-(h,r)\)

大多数文章在讨论LCWA时仅指尾部生成策略。然而，在视觉关系检测领域，关系生成策略是一个流行的选择（参见[zhang2017]和[sharifzadeh2019vrd]）。然而，PyKEEN自PR #602以来还实现了头部生成。

随机局部封闭世界假设

在随机局部封闭世界假设（SLCWA）下进行训练时，从LCWA的头和尾生成策略的联合中随机抽取一个子集被视为负三元组。这样做有几个好处：

1. 减少计算工作量

2. 稀疏更新（即只有几行嵌入受到影响）

3. 能够集成新的负采样策略

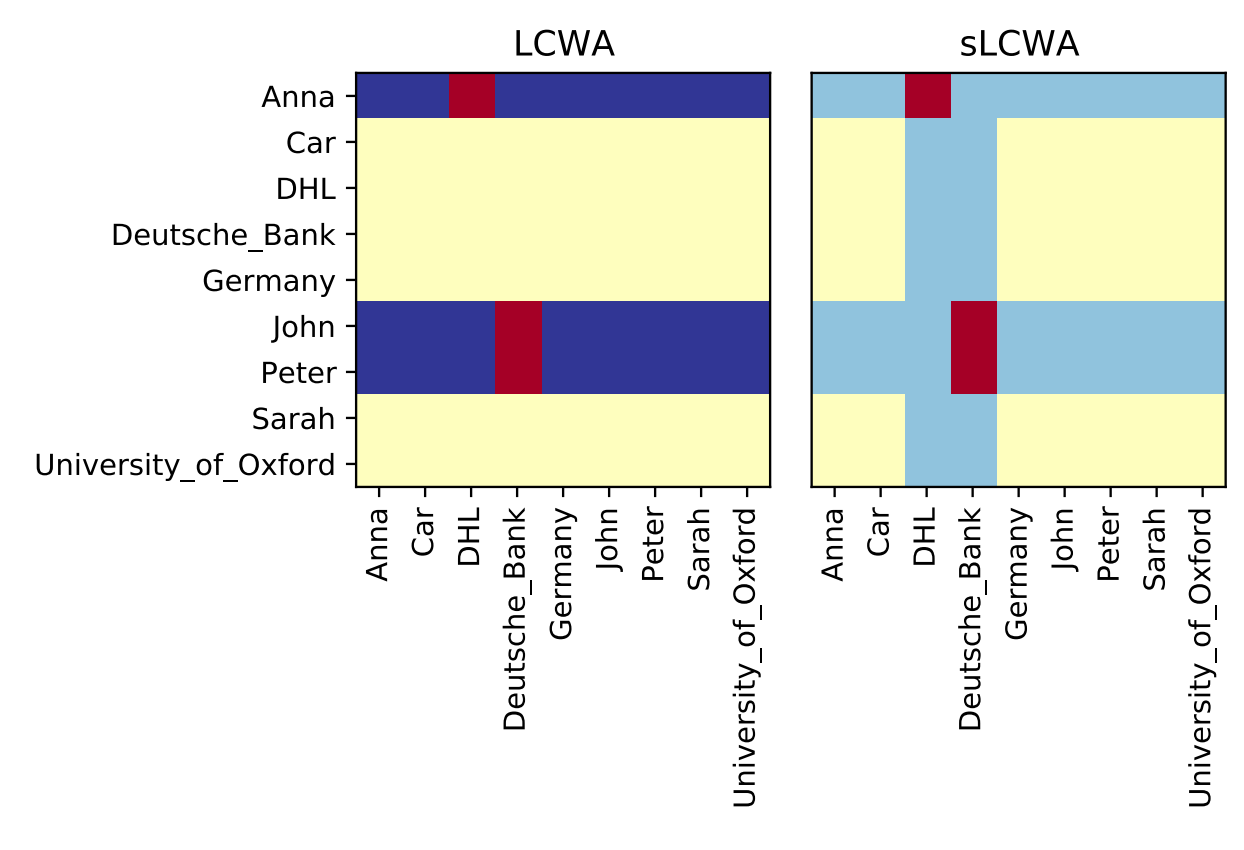
在随机抽样负三元组时，还有两个主要考虑因素：随机抽样策略和正三元组的过滤。关于使用SLCWA进行负抽样的完整指南可以在pykeen.sampling中找到。以下图表来自[ali2020a]，展示了基于给定真实三元组（红色）在LCWA与sLCWA中考虑的不同潜在三元组：

类

TrainingLoop(model, triples_factory[, ...])	一个训练循环。
SLCWATrainingLoop([negative_sampler, ...])	使用随机局部封闭世界假设训练方法的训练循环。
LCWATrainingLoop(*[, target])	一个基于局部封闭世界假设（LCWA）的训练循环。
SymmetricLCWATrainingLoop(model, triples_factory)	一个“对称”的LCWA评分头同时评分头和尾。
NonFiniteLossError	为非有限损失值引发的异常。

变量

training_loop_resolver

训练循环的解析器

类继承图

回调函数

训练回调。

训练回调允许任意扩展pykeen.training.TrainingLoop的功能，而无需对其进行子类化。每个回调实例都有一个loop属性，允许访问父训练循环及其所有属性，包括模型。交互点类似于Keras。

示例

以下是展示如何使用回调任意扩展PyKEEN训练循环的示例。如果您发现TrainingCallback中的钩子无法满足您的需求，请随时提出问题。

报告批次损失

在问题 #333中建议，记录所有批次的损失可能是有用的。这可以通过以下方式实现：

from pykeen.training import TrainingCallback

class BatchLossReportCallback(TrainingCallback):
    def on_batch(self, epoch: int, batch, batch_loss: float):
        print(epoch, batch_loss)

实现梯度裁剪

梯度裁剪是一种用于避免梯度爆炸问题的技术。尽管它非常简单，但它有几个理论意义。

为了重现[schlichtkrull2018]在R-GCN上进行的参考实验，必须在优化器的每一步之前使用梯度裁剪。以下示例展示了如何实现梯度裁剪回调：

from pykeen.training import TrainingCallback
from pykeen.nn.utils import clip_grad_value_

class GradientClippingCallback(TrainingCallback):
    def __init__(self, clip_value: float = 1.0):
        super().__init__()
        self.clip_value = clip_value

    def pre_step(self, **kwargs: Any):
        clip_grad_value_(self.model.parameters(), clip_value=self.clip_value)

类

TrainingCallback()	训练回调的接口。
StopperTrainingCallback(stopper, *, ...[, ...])	一个用于pykeen.stopper.Stopper的适配器。
TrackerTrainingCallback()	一个用于pykeen.trackers.ResultTracker的适配器。
EvaluationLoopTrainingCallback(factory[, ...])	用于使用新式评估循环进行常规评估的回调。
EvaluationTrainingCallback(*, evaluation_triples)	用于定期评估的回调。
CheckpointTrainingCallback([schedule, ...])	在用户指定的周期保存检查点。
MultiTrainingCallback([callbacks, ...])	一个用于同时调用多个训练回调的包装器。
GradientNormClippingTrainingCallback(max_norm)	在优化器步进之前进行梯度裁剪的回调函数，使用torch.nn.utils.clip_grad_norm_()。
GradientAbsClippingTrainingCallback(clip_value)	在优化器步进之前进行梯度裁剪的回调函数，使用torch.nn.utils.clip_grad_value_()。

变量

callback_resolver	训练回调的解析器
TrainingCallbackHint	构建MultiTrainingCallback的提示

类继承图

学习率调度器

PyKEEN 中可用的学习率调度器。

类

LRScheduler(optimizer[, last_epoch, verbose])

在优化过程中调整学习率。

变量

lr_schedulers_hpo_defaults	基于torch.optim.lr_scheduler.LRScheduler的默认策略，用于优化lr_schedulers的超参数。
lr_scheduler_resolver	从类列表中解析。

类继承图