四重#
表示在平面上的一个四边形(也称为“矩形”或“四边形”),定义为四个 Point 对象 ul, ur, ll, lr(方便地称为左上角、右上角、左下角、右下角)的序列。
四边形可以 通过 文本搜索方法 (Page.search_for()) 获得,且它们 用于 定义文本标记注释(例如 see Page.add_squiggly_annot() 和其余方法),以及在多种绘制方法中(例如 Page.draw_quad() / Shape.draw_quad(), Page.draw_oval()/ Shape.draw_quad())。
注意
如果一个矩形的角经过旋转、缩放或平移 矩阵变换,则得到的四边形是矩形(=与矩形全等),即其所有角再次形成90度的角。属性
Quad.is_rectangular检查一个四边形是否可以被视为这种操作的结果。并非所有矩阵都适用:例如,剪切矩阵会产生平行四边形,而不可逆矩阵会产生像三角形或直线这样的“退化”四边形。
属性
Quad.rect获取包围矩形。反之,矩形现在具有属性Rect.quad和IRect.quad来获取它们各自的四边形版本。
方法 / 属性 |
简短描述 |
|---|---|
用矩阵变换 |
|
使用一个点和矩阵进行变换 |
|
左上角点 |
|
右上点 |
|
左下角点 |
|
右下角点 |
|
如果四边形是一个凸集则为真 |
|
如果四元组是一个空集合,则为真 |
|
如果四边形与矩形全等,则为真 |
|
最小包含 Rect |
|
最长的宽度值 |
|
最长的高度值 |
类 API
- class Quad#
- __init__(self)#
- __init__(self, ul, ur, ll, lr)#
- __init__(self, quad)#
- __init__(self, sequence)#
重载构造函数:“ul”、“ur”、“ll”、“lr”代表
point_like对象(四个角), “sequence”是一个包含四个point_like对象的Python序列。如果指定了“quad”,则构造函数会创建它的 新副本。
不带参数时,创建一个由 4 个 Point(0, 0) 复制组成的四边形。
- transform(matrix)#
通过用矩阵变换每个角来修改四边形。
- Parameters:
matrix (matrix_like) – 矩阵.
- morph(fixpoint, matrix)#
(版本 1.17.0 新增) 使用点状作为固定点,以矩阵般的方式“形变”四边形。
- Parameters:
fixpoint (point_like) – 该点。
矩阵 (类似矩阵) – 矩阵。
- Returns:
一个新的四边形(如果这是无限四边形,则不进行操作)。
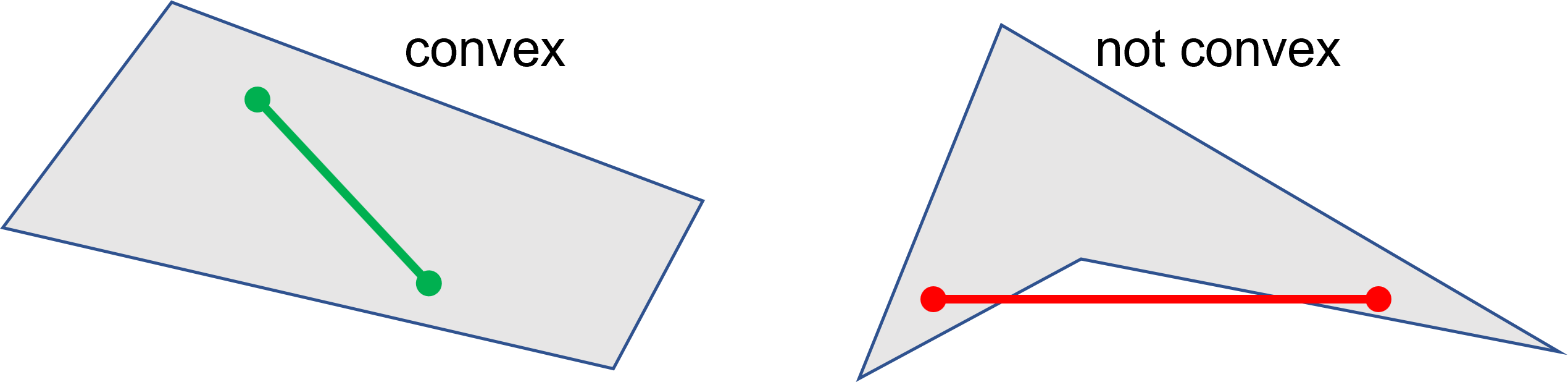
- is_convex#
版本 1.16.1 中的新功能
检查四边形的任意两个点之间的连接线上的所有点是否也属于该四边形。
- Type:
布尔值
- is_empty#
当封闭区域为零时返回真,这意味着四个角中的至少三个在同一条直线上。如果这是假的,四边形可能仍然是退化的,或者根本不看起来像一个四边形(三角形、平行四边形、梯形等)。
- Type:
布尔值
- is_rectangular#
如果所有角都是90度,则为真。这意味着四边形是 凸的且非空。
- Type:
布尔值
- width#
顶部和底部的最大长度。
- Type:
浮点数
- height#
左右两侧的最大长度。
- Type:
浮点数
备注#
该类遵循序列协议,因此组件也可以通过它们的索引进行处理。另请参阅 在 PyMuPDF 中使用 Python 序列作为参数。
代数和包含性检查#
从v1.19.6开始,四边形可以像其他几何对象一样用于代数表达式 - 相关的限制已被解除。特别是,现在所有以下的包含检查组合都是可能的:
{Point | IRect | Rect | Quad} in {IRect | Rect | Quad}
请注意以下有趣的细节:
对于矩形,仅有其左上角点属于它。自v1.19.0起,矩形被定义为“开放”,因此其底部和右边缘不属于它——包括相应的角。但对于四边形并不存在“开放”这样的概念,因此我们有以下有些令人惊讶的推论:
>>> rect.br in rect
False
>>> # but:
>>> rect.br in rect.quad
True