Find #pymupdf on Discord

矩形#

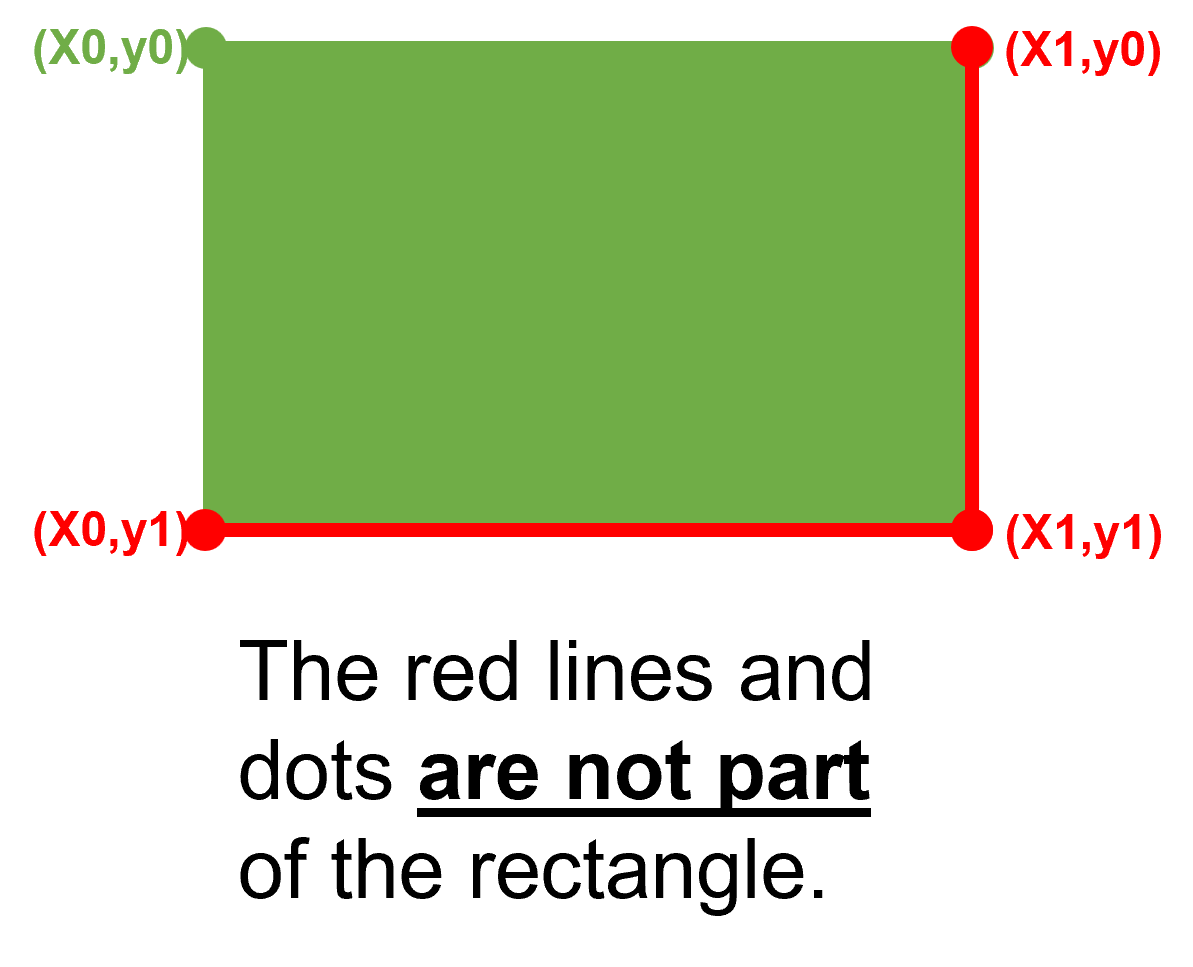
Rect表示由四个浮点数 x0, y0, x1, y1 定义的矩形。它们被视为两个对角线相对点的坐标。前两个数字被视为“左上”角 P_(x0,y0)，而 P_(x1,y1) 被视为“右下”角。然而，这两个属性不一定与它们的直觉含义一致——继续阅读。

以下备注同样适用于 IRect 对象：

在（Py-）MuPDF （和PDF）的意义上，矩形总是具有与x轴或y轴平行的边界。一般的正交四边形不是矩形——与数学定义相反。
构造点可以几乎在平面上的任何位置（几乎！– 见下文）– 它们甚至不需要不同，例如，“左上角”不一定是几何上的“西北”点。
单位为点，72个点为1英寸。
For any given quadruple of numbers, the geometrically “same” rectangle can be defined in four different ways:
1. 矩形(P_(x0,y0), P_(x1,y1))
2. 矩形(P_(x1,y1), P_(x0,y0))
3. 矩形(P_(x0,y1), P_(x1,y0))
4. 矩形(P_(x1,y0), P_(x0,y1))

(在v1.19.0中更改) 因此进行一些分类：

矩形被称为有效，如果 x0 <= x1 和 y0 <= y1 （即，右下角的点位于左上角的 “东南” 位置），否则称为无效。在上述四个选项中，只有第一个 是有效的。请考虑，在 MuPDF 的坐标系统中，y 轴的方向是 从上到下 。无效的矩形在早期版本中被称为无限。
矩形被称为空如果 x0 >= x1 或 y0 >= y1。这意味着， 无效的矩形也总是空。 如果 x0 > x1（分别是 y0 > y1），则 width（或者 height）被 设为零。在之前的版本中，只有当宽度或高度之一为零时，矩形才为空。
矩形坐标 不能超出 从 FZ_MIN_INF_RECT = -2147483648 到 FZ_MAX_INF_RECT = 2147483520 的数值范围。这两个值被选定，因为它们是经过 C 浮点转换往返后仍能保留的最小 / 最大 32 位整数。在以前的版本中，坐标值没有限制。
有正好一个“无限”矩形，由x0 = y0 = FZ_MIN_INF_RECT和x1 = y1 = FZ_MAX_INF_RECT定义。它包含每个其他矩形。它主要用于技术目的——例如，当函数调用应该忽略一个形式上要求的矩形参数时。这个矩形不是空的。
矩形是（半）开放的：右边和底边（包括相应的角）不被视为矩形的一部分。这意味着，只有左上角 (x0, y0) 才能属于矩形 - 其他三个角永远不会属于矩形。一个空的矩形根本不包含任何角。

这是更改的概述。

概念

版本 < 1.19.0

版本 1.19.*

为空

x0 = x1 or y0 = y1

x0 >= x1 or y0 >= y1 – 包含无效矩形

有效

不可用

x0 <= x1 and y0 <= y1

无限

所有矩形，其中 x0 > x1 或 y1 > y0

正好一个无限矩形 / irect!

坐标值

所有数字

FZ_MIN_INF_RECT <= number <= FZ_MAX_INF_RECT

边框，角

是矩形的部分

右下角和边缘 在外面

有新的顶级函数定义无限和标准空矩形及四边形，见 INFINITE_RECT() 以及相关函数。

概念	版本 < 1.19.0	版本 1.19.*
为空	x0 = x1 or y0 = y1	x0 >= x1 or y0 >= y1 – 包含无效矩形
有效	不可用	x0 <= x1 and y0 <= y1
无限	所有矩形，其中 x0 > x1 或 y1 > y0	正好一个无限矩形 / irect!
坐标值	所有数字	`FZ_MIN_INF_RECT <= number <= FZ_MAX_INF_RECT`
边框，角	是矩形的部分	右下角和边缘在外面

方法 / 属性	简短描述
`Rect.contains()`	检查点类型和矩形类型的包含关系
`Rect.get_area()`	计算矩形面积
`Rect.include_point()`	扩大矩形以包含一个点
`Rect.include_rect()`	放大矩形以包含另一个矩形
`Rect.intersect()`	与另一个矩形的公共部分
`Rect.intersects()`	检查非空交集
`Rect.morph()`	使用一个点和一个矩阵进行变换
`Rect.torect()`	转换为另一个矩形的矩阵
`Rect.norm()`	欧几里得范数
`Rect.normalize()`	使矩形有效
`Rect.round()`	创建包含最小的 IRect 矩形
`Rect.transform()`	使用矩阵变换矩形
`Rect.bottom_left`	左下角点，同义词 bl
`Rect.bottom_right`	右下角点，同义词 br
`Rect.height`	矩形高度
`Rect.irect`	等于方法 round() 的结果
`Rect.is_empty`	矩形是否为空
`Rect.is_valid`	矩形是否有效
`Rect.is_infinite`	矩形是否是无限的
`Rect.top_left`	左上角点，同义词 tl
`Rect.top_right`	右上角点，同义词 tr
`Rect.quad`	Quad 由矩形角落构成
`Rect.width`	矩形宽度
`Rect.x0`	左上角的 x 坐标
`Rect.x1`	右下角的 x 坐标
`Rect.y0`	顶部角的 y 坐标
`Rect.y1`	底部角的 y 坐标

类 API

class Rect#

__init__(self)#

__init__(self, x0, y0, x1, y1)#

__init__(self, top_left, bottom_right)#

__init__(self, top_left, x1, y1)#

__init__(self, x0, y0, bottom_right)#

__init__(self, rect)#

__init__(self, sequence)#

重载构造函数： top_left, bottom_right 代表 point_like 对象，“sequence” 是 4 个数字的 Python 序列类型（见在 PyMuPDF 中使用 Python 序列作为参数），“rect” 代表另一个 rect_like，而其他参数代表坐标。

如果指定了“rect”，构造函数将创建一个新的副本。

没有参数时，创建一个空矩形 Rect(0.0, 0.0, 0.0, 0.0)。

round()#

创建最小的包含 IRect。这并不与简单地四舍五入矩形的边缘相同：左上角向上和向左四舍五入，而右下角向下和向右四舍五入。

>>> pymupdf.Rect(0.5, -0.01, 123.88, 455.123456).round()
IRect(0, -1, 124, 456)

如果矩形是空的，结果也为空。
可能的悖论： 结果可能为空，即使矩形不为空！在这种情况下，结果显然不包含该矩形。这是因为 MuPDF 的算法允许一个小的容忍度 (1e-3)。示例：

>>> r = pymupdf.Rect(100, 100, 200, 100.001)
>>> r.is_empty  # rect is NOT empty
False
>>> r.round()  # but its irect IS empty!
pymupdf.IRect(100, 100, 200, 100)
>>> r.round().is_empty
True

Return type:: IRect

transform(m)#

使用矩阵变换矩形并替换原始。如果矩形为空或无限，这将不执行任何操作。

Parameters:: m (Matrix) – 变换的矩阵。
Return type:: 矩形
Returns:: 包含变换后的原始对象的最小矩形。

intersect(r)#

当前矩形与r的交集（公共矩形区域，包含在两者中的最大矩形）被计算并替换当前矩形。如果任一矩形为空，则结果也为空。如果r是无限的，则这是一个无操作。如果矩形是（数学上）不相交的集合，则结果是无效的。如果结果有效但为空，则矩形在一个角落或（部分）边上相接触。

Parameters:: r (Rect) – 第二个矩形

include_rect(r)#

包含当前矩形和r的最小矩形被计算出来并替换当前矩形。如果任一矩形是无限的，结果也是无限的。如果其中一个是空的，另一个将被视为结果。

Parameters:: r (Rect) – 第二个矩形

include_point(p)#

包含当前矩形和点 p 的最小矩形被计算并 替换当前的 矩形。 无限矩形保持不变。 要创建一个包含一系列点的矩形，可以从（空的） pymupdf.Rect(p1, p1) 开始，并连续包含剩余的点。

Parameters:: p (Point) – 要包含的点。

get_area([unit])#

计算矩形的面积，且无参数，等于 abs(rect)。像一个空矩形，一无限矩形的面积也是零。因此，pymupdf.Rect(p1, p2) 和 pymupdf.Rect(p2, p1) 中至少有一个的面积为零。

Parameters:: 单位 (字符串) – 指定所需的单位：分别为 px（像素，默认）、in（英寸）、cm（厘米）或 mm（毫米）。
Return type:: 浮点数

contains(x)#

检查 x 是否包含在矩形内。它可以是 IRect、Rect、Point 或数字。如果 x 是一个空矩形，那么这总是为真。如果矩形是空的，对于所有非空矩形和所有点，这总是 False。x in rect 和 rect.contains(x) 是等价的。

Parameters:: x (rect_like 或 point_like.) – 要检查的对象。
Return type:: 布尔值

intersects(r)#

检查矩形和一个 rect_like “r” 是否包含一个共同的非空 Rect。如果其中任一个是无限或空的，这将始终为 False。

Parameters:: r (rect_like) – 要检查的矩形。
Return type:: 布尔值

torect(rect)#

版本 1.19.3 新增

计算将这个矩形转换为给定矩形的矩阵。

Parameters:: rect (rect_like) – 目标矩形。必须非空且有限。
Return type:: 矩阵
Returns:: 一个矩阵 mat，使得 self * mat = rect。可以用于在页面和像素图坐标之间进行转换。例如，查看这里的使用示例如何使用像素图：检查文本可见性。

morph(fixpoint, matrix)#

1.17.0 版本的新功能

在使用固定点 fixpoint 将矩阵应用于矩形后返回一个新的四边形。

Parameters:

fixpoint (point_like) – 固定点。
矩阵 (类似矩阵) – 矩阵。

Returns:

一个新的 Quad。这是一个用于同名四重积分方法的包装器。如果是无限的，将返回无限四重积分。

norm()#

版本 1.16.0 中的新功能

返回将矩形视为四个数字的向量的欧几里得范数。

normalize()#: 替换矩形为其有效版本。这是通过打乱矩形的角来完成的。在此方法完成后，右下角确实会位于左上角的东南方向（但可能仍然是空的）。

irect#: 等于方法 round() 的结果。

top_left#

tl#

等于 Point(x0, y0).

Type:: 点

top_right#

tr#

等于 Point(x1, y0).

Type:: 点

bottom_left#

bl#

等于 Point(x0, y1).

Type:: 点

bottom_right#

br#

等于 Point(x1, y1).

Type:: 点

quad#

四边形 Quad(rect.tl, rect.tr, rect.bl, rect.br).

Type:: 四元

width#

矩形的宽度。等于 max(x1 - x0, 0).

Return type:: 浮点数

height#

矩形的高度。等于 max(y1 - y0, 0).

Return type:: 浮点数

x0#

左角的X坐标。

Type:: 浮点数

y0#

顶部角的Y坐标。

Type:: 浮点数

x1#

右角的X坐标。

Type:: 浮点数

y1#

底部角的Y坐标。

Type:: 浮点数

is_infinite#

True 如果这是无限矩形。

Type:: 布尔值

is_empty#

True 如果矩形是空的。

Type:: 布尔值

is_valid#

True 如果矩形有效。

Type:: 布尔值

注意

这个类遵循 Python 序列协议，因此组件也可以通过它们的索引访问。同时请参考在 PyMuPDF 中使用 Python 序列作为参数。
矩形可以与算术运算符一起使用 - 参见章节几何对象的运算符代数。

Do you have any feedback on this page?

本软件按原样提供，不作任何明示或暗示的担保。该软件根据许可证分发，除非按照该许可证的条款明确授权，否则不得复制、修改或分发。有关许可信息，请参阅artifex.com或联系Artifex Software Inc.，地址：39 Mesa Street, Suite 108A, San Francisco CA 94129, United States以获取更多信息。