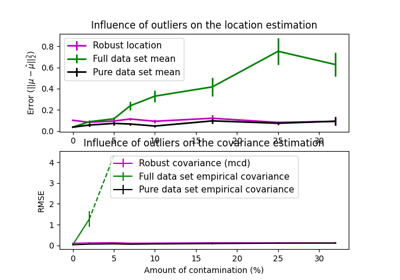
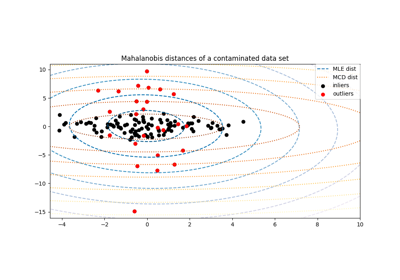
MinCovDet#
- class sklearn.covariance.MinCovDet(*, store_precision=True, assume_centered=False, support_fraction=None, random_state=None)#
最小协方差决定(MCD):协方差的稳健估计器。
最小协方差决定协方差估计器适用于高斯分布数据,但在从单峰对称分布中抽取的数据上仍然相关。它不适用于多峰数据(用于拟合MinCovDet对象的算法在这种情况下可能会失败)。 应考虑投影追踪方法来处理多峰数据集。
更多信息请参阅 用户指南 。
- Parameters:
- store_precisionbool, default=True
指定是否存储估计的精度。
- assume_centeredbool, default=False
如果为True,则计算稳健位置和协方差估计的支持,并从中重新计算协方差估计,而不对数据进行中心化。 适用于均值显著等于零但并非完全为零的数据。 如果为False,则直接使用FastMCD算法计算稳健位置和协方差,不进行额外处理。
- support_fractionfloat, default=None
要在原始MCD估计的支持中包含的点的比例。默认为None,这意味着在算法中将使用support_fraction的最小值:
(n_samples + n_features + 1) / 2 * n_samples。该参数必须在(0, 1]范围内。- random_stateint, RandomState instance or None, default=None
确定用于洗牌数据的伪随机数生成器。 传递一个int以在多次函数调用中获得可重复的结果。 请参阅 Glossary 。
- Attributes:
- raw_location_ndarray of shape (n_features,)
在修正和重新加权之前的原始稳健估计位置。
- raw_covariance_ndarray of shape (n_features, n_features)
在修正和重新加权之前的原始稳健估计协方差。
- raw_support_ndarray of shape (n_samples,)
用于计算原始稳健位置和形状估计的观测值的掩码,在修正和重新加权之前。
- location_ndarray of shape (n_features,)
估计的稳健位置。
- covariance_ndarray of shape (n_features, n_features)
估计的稳健协方差矩阵。
- precision_ndarray of shape (n_features, n_features)
估计的伪逆矩阵。 (仅在store_precision为True时存储)
- support_ndarray of shape (n_samples,)
用于计算稳健位置和形状估计的观测值的掩码。
- dist_ndarray of shape (n_samples,)
训练集(在其上调用
fit)观测值的马氏距离。- n_features_in_int
在 fit 期间看到的特征数量。
Added in version 0.24.
- feature_names_in_ndarray of shape (
n_features_in_,) 在 fit 期间看到的特征名称。仅当
X的特征名称均为字符串时定义。Added in version 1.0.
See also
EllipticEnvelope用于检测高斯分布数据集中的异常值的对象。
EmpiricalCovariance最大似然协方差估计器。
GraphicalLasso使用l1惩罚估计器的稀疏逆协方差估计。
GraphicalLassoCV带有l1惩罚交叉验证选择的稀疏逆协方差。
LedoitWolfLedoitWolf估计器。
OASOracle近似收缩估计器。
ShrunkCovariance带有收缩的协方差估计器。
References
[Rouseeuw1984]P. J. Rousseeuw. Least median of squares regression. J. Am Stat Ass, 79:871, 1984.
[Rousseeuw]A Fast Algorithm for the Minimum Covariance Determinant Estimator, 1999, American Statistical Association and the American Society for Quality, TECHNOMETRICS
[ButlerDavies]R. W. Butler, P. L. Davies and M. Jhun, Asymptotics For The Minimum Covariance Determinant Estimator, The Annals of Statistics, 1993, Vol. 21, No. 3, 1385-1400
Examples
>>> import numpy as np >>> from sklearn.covariance import MinCovDet >>> from sklearn.datasets import make_gaussian_quantiles >>> real_cov = np.array([[.8, .3], ... [.3, .4]]) >>> rng = np.random.RandomState(0) >>> X = rng.multivariate_normal(mean=[0, 0], ... cov=real_cov, ... size=500) >>> cov = MinCovDet(random_state=0).fit(X) >>> cov.covariance_ array([[0.7411..., 0.2535...], [0.2535..., 0.3053...]]) >>> cov.location_ array([0.0813... , 0.0427...])
- correct_covariance(data)#
应用对原始最小协方差行列式估计的修正。
使用Rousseeuw和Van Driessen在[RVD]中建议的经验修正因子进行修正。
- Parameters:
- data形状为(n_samples, n_features)的类数组
数据矩阵,包含p个特征和n个样本。 数据集必须是用于计算原始估计的数据集。
- Returns:
- covariance_corrected形状为(n_features, n_features)的ndarray
修正后的鲁棒协方差估计。
References
[RVD]一种用于最小协方差行列式估计器的快速算法,1999年,美国统计协会 和美国质量学会,TECHNOMETRICS
- error_norm(comp_cov, norm='frobenius', scaling=True, squared=True)#
计算两个协方差估计器之间的均方误差。
- Parameters:
- comp_cov形状为 (n_features, n_features) 的类数组
要比较的协方差。
- norm{“frobenius”, “spectral”}, 默认=”frobenius”
用于计算误差的范数类型。可用的误差类型: - ‘frobenius’ (默认): sqrt(tr(A^t.A)) - ‘spectral’: sqrt(max(eigenvalues(A^t.A)) 其中 A 是误差
(comp_cov - self.covariance_)。- scalingbool, 默认=True
如果为 True(默认),平方误差范数除以 n_features。 如果为 False,平方误差范数不进行缩放。
- squaredbool, 默认=True
是否计算平方误差范数或误差范数。 如果为 True(默认),返回平方误差范数。 如果为 False,返回误差范数。
- Returns:
- resultfloat
self和comp_cov协方差估计器之间的均方误差(以 Frobenius 范数为意义)。
- fit(X, y=None)#
拟合一个使用FastMCD算法的最小协方差行列式。
- Parameters:
- X形状为 (n_samples, n_features) 的类数组
训练数据,其中
n_samples是样本数量 且n_features是特征数量。- y忽略
未使用,为了API一致性而存在。
- Returns:
- self对象
返回实例本身。
- get_metadata_routing()#
获取此对象的元数据路由。
请查看 用户指南 以了解路由机制的工作原理。
- Returns:
- routingMetadataRequest
MetadataRequest封装的 路由信息。
- get_params(deep=True)#
获取此估计器的参数。
- Parameters:
- deepbool, 默认=True
如果为True,将返回此估计器和包含的子对象(也是估计器)的参数。
- Returns:
- paramsdict
参数名称映射到它们的值。
- get_precision()#
获取精度矩阵的方法。
- Returns:
- precision_array-like of shape (n_features, n_features)
与当前协方差对象相关的精度矩阵。
- mahalanobis(X)#
计算给定观测值的马氏距离平方。
- Parameters:
- X形状为 (n_samples, n_features) 的类数组
我们计算其马氏距离的观测值。假设这些观测值是从与fit中使用的数据相同的分布中抽取的。
- Returns:
- dist形状为 (n_samples,) 的 ndarray
观测值的马氏距离平方。
- reweight_covariance(data)#
重新加权原始最小协方差行列式估计。
使用Rousseeuw的方法重新加权观测值(相当于在计算位置和协方差估计之前从数据集中删除异常观测值),该方法在[RVDriessen]中描述。
- Parameters:
- data形状为(n_samples, n_features)的类数组
数据矩阵,包含p个特征和n个样本。 数据集必须是用于计算原始估计的数据集。
- Returns:
- location_reweighted形状为(n_features,)的ndarray
重新加权的稳健位置估计。
- covariance_reweighted形状为(n_features, n_features)的ndarray
重新加权的稳健协方差估计。
- support_reweighted形状为(n_samples,)的ndarray,dtype=bool
用于计算重新加权的稳健位置和协方差估计的观测值的掩码。
References
[RVDriessen]一种用于最小协方差行列式估计器的快速算法,1999年,美国统计协会和美国质量学会,TECHNOMETRICS
- score(X_test, y=None)#
计算在估计的高斯模型下
X_test的对数似然。高斯模型由其均值和协方差矩阵定义,分别由
self.location_和self.covariance_表示。- Parameters:
- X_test类数组,形状为 (n_samples, n_features)
我们计算其似然的测试数据,其中
n_samples是样本数量,n_features是特征数量。X_test假设是从与拟合中使用的数据相同的分布中抽取的(包括中心化)。- y忽略
未使用,为保持API一致性而存在。
- Returns:
- resfloat
以
self.location_和self.covariance_分别为高斯模型均值和协方差矩阵估计量的X_test的对数似然。
- set_params(**params)#
设置此估计器的参数。
该方法适用于简单估计器以及嵌套对象(例如
Pipeline)。后者具有形式为<component>__<parameter>的参数,以便可以更新嵌套对象的每个组件。- Parameters:
- **paramsdict
估计器参数。
- Returns:
- selfestimator instance
估计器实例。
- set_score_request(*, X_test: bool | None | str = '$UNCHANGED$') MinCovDet#
Request metadata passed to the
scoremethod.Note that this method is only relevant if
enable_metadata_routing=True(seesklearn.set_config). Please see User Guide on how the routing mechanism works.The options for each parameter are:
True: metadata is requested, and passed toscoreif provided. The request is ignored if metadata is not provided.False: metadata is not requested and the meta-estimator will not pass it toscore.None: metadata is not requested, and the meta-estimator will raise an error if the user provides it.str: metadata should be passed to the meta-estimator with this given alias instead of the original name.
The default (
sklearn.utils.metadata_routing.UNCHANGED) retains the existing request. This allows you to change the request for some parameters and not others.Added in version 1.3.
Note
This method is only relevant if this estimator is used as a sub-estimator of a meta-estimator, e.g. used inside a
Pipeline. Otherwise it has no effect.- Parameters:
- X_teststr, True, False, or None, default=sklearn.utils.metadata_routing.UNCHANGED
Metadata routing for
X_testparameter inscore.
- Returns:
- selfobject
The updated object.