浅层节点嵌入

在本教程中，我们将更详细地了解如何通过PyG以无监督的方式学习浅层节点嵌入。

介绍

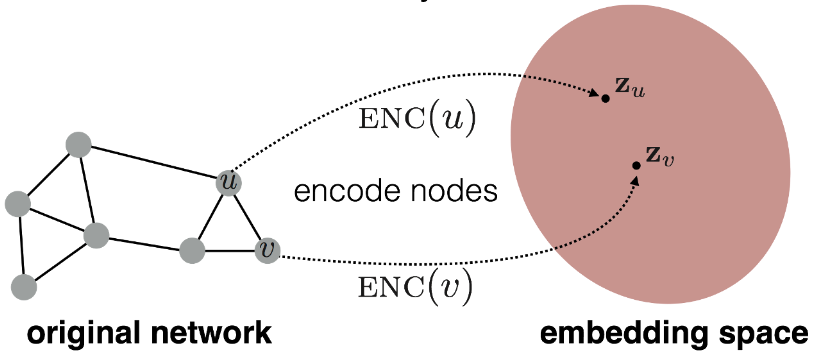
浅层节点嵌入（例如， Node2Vec）和深层节点嵌入（例如， GNNs）之间的关键区别在于编码器的选择 \(\textrm{ENC}(v, \mathcal{G}) = \mathbf{z}_v \in \mathbb{R}^d\)。具体来说，浅层节点嵌入技术依赖于通过浅层嵌入查找表将节点嵌入到低维向量表示 \(\mathbf{z}_v\) 中，以最大化保留邻域的可能性，即附近的节点应获得相似的嵌入，而远处的节点应获得不同的嵌入。这些技术推广了著名的 SkipGram 模型，用于获取低维词嵌入，其中词的序列现在被解释为节点的序列，例如， 通过随机生成的游走给出：

具体来说，给定一个从节点 \(v \in \mathcal{V}\) 开始、长度为 \(k\) 的随机游走 \(\mathcal{W} = (v_{\pi(1)}, \ldots, v_{\pi_(k)})\)，目标是在给定节点 \(v\) 的情况下，最大化观察到节点 \(v_{\pi(i)}\) 的可能性。这个目标可以通过对比学习场景中的随机梯度下降来高效训练。

\[\mathcal{L} = \sum_{w \in \mathcal{W}} - \log \left(\sigma(\mathbf{z}_v^{\top} \mathbf{z}_w) \right) + \sum_{w \sim \mathcal{V} \setminus \mathcal{W}} - \log \left( 1 - \sigma(\mathbf{z}_v^{\top} \mathbf{z}_w) \right),\]

其中不存在的路径（所谓的负例）被采样并联合训练，\(\sigma\)表示\(\textrm{sigmoid}\)函数。值得注意的是，嵌入之间的点积\(\mathbf{z}_v^{\top} \mathbf{z}_w\)通常用于衡量相似性，但其他相似性度量也适用。

重要的是，浅层节点嵌入是以无监督的方式进行训练的，最终可以用作给定下游任务的输入，例如，在节点级任务中，\(\mathbf{z}_v\)可以直接用作最终分类器的输入。对于边级任务，边级表示可以通过平均\(\frac{1}{2} (\mathbf{z}_v + \mathbf{z}_w)\)或通过Hadamard积\(\mathbf{z}_v \odot \mathbf{z}_w\)获得。

尽管节点嵌入技术简单，但它们也存在一些缺点。特别是，它们无法整合附加在节点和边上的丰富特征信息，并且不能轻易应用于未见过的图，因为可学习参数固定于特定图的节点上（这使得这种方法本质上是传导性的，并且由于\(\mathcal{O}(|\mathcal{V}| \cdot d)\)参数复杂性而难以扩展）。然而，它仍然是一种常用的技术，用于将图结构信息保存到固定大小的向量中，并且在初始节点特征集不丰富的情况下，也常用于生成GNN的输入以进行进一步处理。

Node2Vec

注意

在本教程的这一部分中，我们将学习如何使用PyG的Node2Vec模块为同质图生成节点嵌入。代码可以在examples/node2vec.py中找到，也可以作为Google Colab教程笔记本使用。

Node2Vec 是一种用于学习浅层节点嵌入的方法，它允许基于广度优先或深度优先采样器灵活控制随机游走过程。特别是，其参数 p 决定了在游走中立即重新访问节点的可能性，而其参数 q 则在广度优先和深度优先策略之间进行插值。

开始示例之前，让我们先加载所需的包和我们将要使用的数据：

from torch_geometric.nn import Node2Vec

data = Planetoid('./data/Planetoid', name='Cora')[0]

我们现在准备初始化我们的Node2Vec模块：

import torch
from torch_geometric.nn import Node2Vec

device = 'cuda' if torch.cuda.is_available() else 'cpu'

model = Node2Vec(
    data.edge_index,
    embedding_dim=128,
    walks_per_node=10,
    walk_length=20,
    context_size=10,
    p=1.0,
    q=1.0,
    num_negative_samples=1,
).to(device)

optimizer = torch.optim.Adam(model.parameters(), lr=0.01)

Node2Vec 将图结构 edge_index 作为输入（但不包括其任何特征信息），浅层嵌入的 embedding_dim，以及其他参数来控制随机游走和负采样过程。特别是，walks_per_node 和 walk_length 分别指定了每个节点执行的游走次数及其长度。 context_size 表示游走中有多少个节点实际用于梯度优化，即 Node2Vec 在每个采样的游走上滑动，并将它们分割成大小为 context_size 的窗口。如前所述，p 和 q 表示如何生成随机游走。最后，num_negative_samples 指定了每个正游走要生成多少个负游走。

初始化后，我们可以立即开始训练我们的Node2Vec模型。我们首先创建一个数据加载器，它将为我们生成正负随机游走：

loader = model.loader(batch_size=128, shuffle=True, num_workers=4)

要生成随机游走，我们可以简单地遍历数据加载器，例如：

pos_rw, neg_rw = next(iter(loader))

在这里，pos_rw 将包含正随机游走的节点索引，而 neg_rw 将包含负游走的节点索引。特别是，pos_rw 是一个形状为 [batch_size * walks_per_node * (2 + walk_length - context_size), context_size] 的二维矩阵，而 neg_rw 是一个形状为 [num_negative_samples * pos_rw.size(0), context_size] 的二维矩阵。

使用这个loader和内置的对比loss()函数，我们可以定义我们的train()函数如下：

def train():
    model.train()
    total_loss = 0
    for pos_rw, neg_rw in loader:
        optimizer.zero_grad()
        loss = model.loss(pos_rw.to(device), neg_rw.to(device))
        loss.backward()
        optimizer.step()
        total_loss += loss.item()
    return total_loss / len(loader)

完成训练后，我们可以从模型中获取最终的节点嵌入，如下所示：

z = model()  # Full node-level embeddings.
z = model(torch.tensor([0, 1, 2]))  # Embeddings of first three nodes.

MetaPath2Vec

注意

在本教程的这一部分中，我们将学习如何使用PyG的MetaPath2Vec模块为异构图生成节点嵌入。代码可以在examples/hetero/metapath2vec.py找到，也可以作为Google Colab教程笔记本使用。

Node2Vec 的扩展是 MetaPath2Vec 模型，用于异构图。 MetaPath2Vec 的工作方式与 Node2Vec 类似，但期望输入一个边索引的字典（保存图中每种边类型的 edge_index），并根据给定的 metapath 公式进行随机游走采样，例如，

metapath = [
    ('author', 'writes', 'paper'),
    ('paper', 'published_in', 'venue'),
    ('venue', 'publishes', 'paper'),
    ('paper', 'written_by', 'author'),
]

表示从作者节点到论文节点再到会议节点，然后回到论文节点和作者节点进行随机游走采样。否则，模型的初始化和训练与Node2Vec情况相同。