在布洛赫球上绘图
介绍
在研究两级系统的动力学时,通常通过将状态向量或密度矩阵绘制在布洛赫球上来可视化系统的状态。在QuTiP中,有一个类可以方便地创建和操作布洛赫球上的数据集,包括向量和数据点。
布洛赫类
在QuTiP中,创建布洛赫球可以通过调用以下任一方法实现:
b = qutip.Bloch()
这将加载一个Bloch类的实例。
在深入了解这些对象的细节之前,我们可以简单地通过以下方式绘制与这些实例相关的空白布洛赫球体:
b.render()
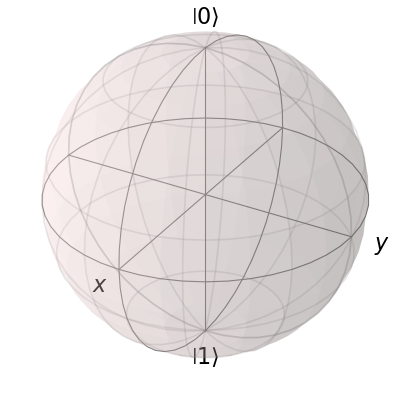
除了show命令外,请参阅Bloch的API文档以获取其他可用功能的完整列表。
例如,我们可以添加一个数据点:
pnt = [1/np.sqrt(3), 1/np.sqrt(3), 1/np.sqrt(3)]
b.add_points(pnt)
b.render()
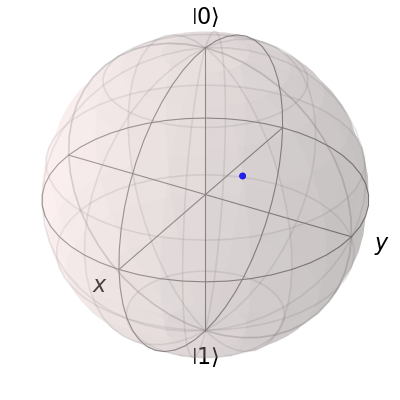
然后是一个单独的向量:
b.fig.clf()
vec = [0, 1, 0]
b.add_vectors(vec)
b.render()

然后添加另一个对应于\(\left|\rm up \right>\)状态的向量:
up = qutip.basis(2, 0)
b.add_states(up)
b.render()
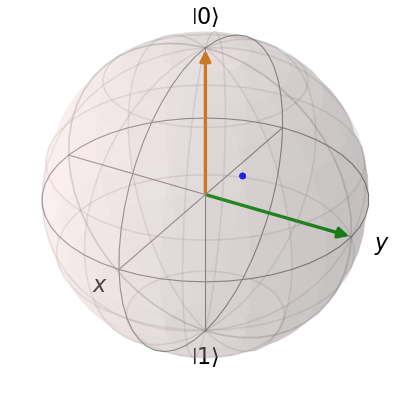
请注意,当我们添加多个向量(或数据点)时,后面的数据集将自动应用不同的颜色(模4)。 总的来说,用于构建我们的布洛赫球体(包含一个向量、一个状态和一个数据点)的代码如下:
b = qutip.Bloch()
pnt = [1./np.sqrt(3), 1./np.sqrt(3), 1./np.sqrt(3)]
b.add_points(pnt)
vec = [0, 1, 0]
b.add_vectors(vec)
up = qutip.basis(2, 0)
b.add_states(up)
b.render()
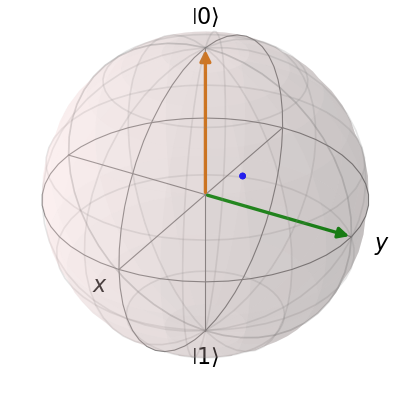
在这里,我们移除了多余的show()命令。
我们也可以通过传递列表或数组而不是单个元素来同时绘制多个点、向量和状态。在给出示例之前,我们可以使用clear()命令从我们的Bloch球体中移除当前数据,而不是创建一个新实例:
b.clear()
b.render()
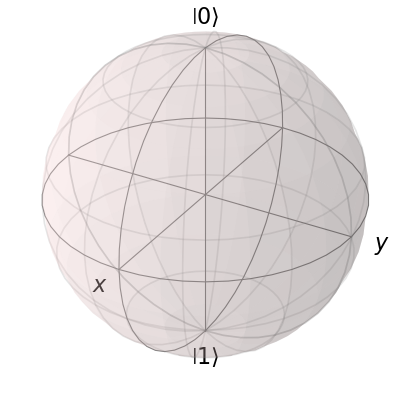
现在在同一个布洛赫球上,我们可以绘制与x、y和z方向相关的三个状态:
x = (qutip.basis(2, 0) + (1+0j)*qutip.basis(2, 1)).unit()
y = (qutip.basis(2, 0) + (0+1j)*qutip.basis(2, 1)).unit()
z = (qutip.basis(2, 0) + (0+0j)*qutip.basis(2, 1)).unit()
b.add_states([x, y, z])
b.render()

类似的方法适用于添加向量:
b.clear()
vec = [[1, 0, 0], [0, 1, 0], [0, 0, 1]]
b.add_vectors(vec)
b.render()
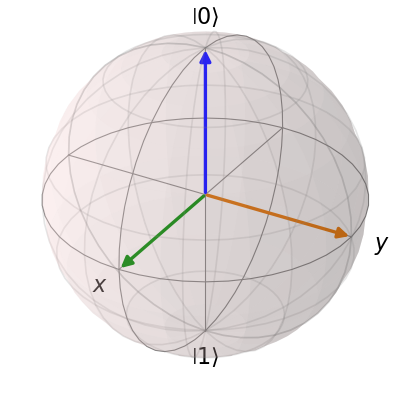
您还可以添加线条和弧线:
b.add_line(x, y)
b.add_arc(y, z)
b.render()
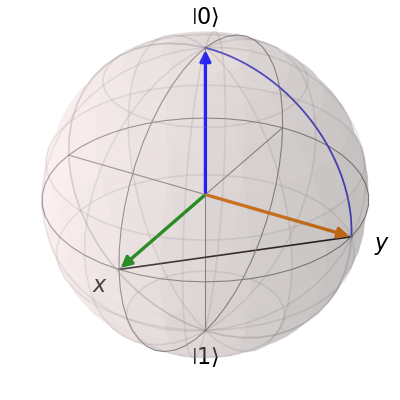
在布洛赫球上添加多个点与添加多个状态或向量略有不同。例如,让我们在赤道周围添加一组20个点(在调用clear()之后):
b.clear()
th = np.linspace(0, 2*np.pi, 20)
xp = np.cos(th)
yp = np.sin(th)
zp = np.zeros(20)
pnts = [xp, yp, zp]
b.add_points(pnts)
b.render()
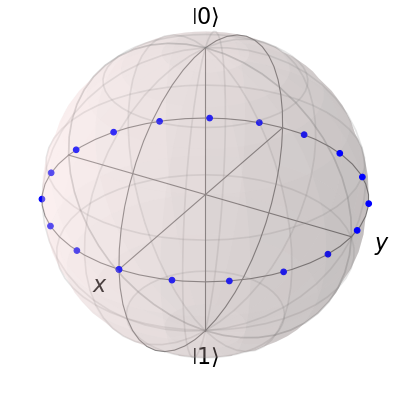
请注意,与状态或向量不同,每个点保持与初始点相同的颜色。这是因为默认情况下,使用add_points函数添加多个数据点被解释为在不同时间绘制的单个数据点(单个量子比特状态)。这在可视化量子比特的动态时非常有用。示例中给出了一个例子。如果我们想要绘制额外的量子比特状态,我们可以调用额外的add_points函数:
xz = np.zeros(20)
yz = np.sin(th)
zz = np.cos(th)
b.add_points([xz, yz, zz])
b.render()

数据点的颜色和形状由Bloch类自动变化。注意每组数据的颜色和点标记是如何变化的。再次强调,我们必须调用add_points两次,因为add_points函数不支持添加多组数据点。
如果我们想要改变点的颜色怎么办。我们可以告诉qutip.bloch.Bloch类根据b.point_color列表中列出的颜色来改变每个点的颜色(参见下面的配置Bloch球)。同样在clear()之后:
b.clear()
xp = np.cos(th)
yp = np.sin(th)
zp = np.zeros(20)
pnts = [xp, yp, zp]
b.add_points(pnts, 'm') # <-- add a 'm' string to signify 'multi' colored points
b.render()
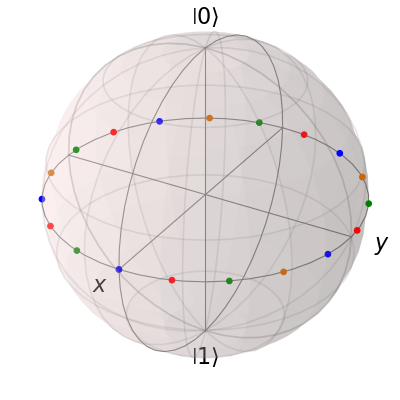
现在,数据点循环使用各种预定义的颜色。现在让我们添加另一组点,但这次我们希望这组点是单一颜色,表示一个量子位从\(\left|\rm up\right>\)状态转变为\(\left|\rm down\right>\)状态在y-z平面中:
xz = np.zeros(20)
yz = np.sin(th)
zz = np.cos(th)
b.add_points([xz, yz, zz]) # no 'm'
b.render()
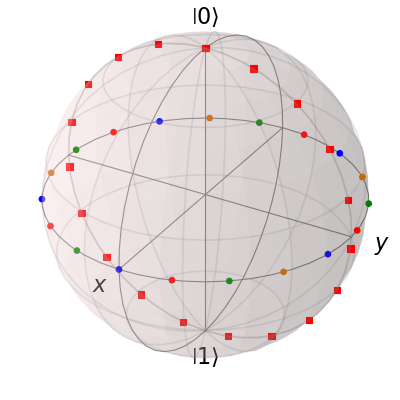
在示例中还展示了一种更巧妙的使用这种“多”颜色功能的方法,我们将标记的颜色设置为时间的函数。
配置布洛赫球
Bloch 类选项
在上一节的最后,我们看到在布洛赫球上绘制的数据的颜色和标记形状会根据添加的点和向量的数量自动变化。但是,如果你想要不同的颜色选择,或者你希望你的球体是紫色并带有不同的轴标签呢?那么你很幸运,因为Bloch类有22个可以控制的属性。假设b=Bloch():
属性 |
功能 |
默认设置 |
|---|---|---|
b.axes |
用于动画的Matplotlib轴实例。通过 |
|
b.fig |
用户提供的Matplotlib Figure实例。通过 |
|
b.font_color |
字体颜色 |
‘black’ |
b.font_size |
字体大小 |
20 |
b.frame_alpha |
线框的透明度 |
0.1 |
b.frame_color |
线框的颜色 |
‘gray’ |
b.frame_width |
线框的宽度 |
1 |
b.point_color |
用于循环显示 Bloch 点标记的颜色列表 |
|
b.point_marker |
循环使用的点标记形状列表 |
|
b.point_size |
点标记大小的列表(并非所有标记在绘制时看起来大小相同) |
|
b.sphere_alpha |
布洛赫球的透明度 |
0.2 |
b.sphere_color |
布洛赫球的颜色 |
|
b.size |
设置图形窗口的大小 |
|
b.vector_color |
用于循环显示Bloch矢量的颜色列表 |
|
b.vector_width |
布洛赫向量的宽度 |
4 |
b.view |
方位角和仰角视角 |
|
b.xlabel |
x轴标签 |
|
b.xlpos |
x轴标签的位置 |
|
b.ylabel |
y轴标签 |
|
b.ylpos |
y轴标签的位置 |
|
b.zlabel |
z轴标签 |
|
b.zlpos |
z轴标签的位置 |
|
这些属性也可以通过打印命令访问:
>>> b = qutip.Bloch()
>>> print(b)
Bloch data:
-----------
Number of points: 0
Number of vectors: 0
Bloch sphere properties:
------------------------
font_color: black
font_size: 20
frame_alpha: 0.2
frame_color: gray
frame_width: 1
point_color: ['b', 'r', 'g', '#CC6600']
point_marker: ['o', 's', 'd', '^']
point_size: [25, 32, 35, 45]
sphere_alpha: 0.2
sphere_color: #FFDDDD
figsize: [5, 5]
vector_color: ['g', '#CC6600', 'b', 'r']
vector_width: 3
vector_style: -|>
vector_mutation: 20
view: [-60, 30]
xlabel: ['$x$', '']
xlpos: [1.2, -1.2]
ylabel: ['$y$', '']
ylpos: [1.2, -1.2]
zlabel: ['$\\left|0\\right>$', '$\\left|1\\right>$']
zlpos: [1.2, -1.2]
使用布洛赫球进行动画
Bloch 类从一开始就被设计用来生成动画。要为一组向量或数据点制作动画,基本思路是:在时间 t1 绘制数据,保存球体,清除球体,在 t2 绘制数据,…… Bloch 球体将根据对象保存的次数自动编号输出文件(这存储在 b.savenum 中)。在 Bloch 球体上制作数据动画的最简单方法是使用 save() 方法并生成一系列图像以转换为动画。然而,从 Matplotlib 1.1 版本开始,创建动画是内置的。我们将通过在 Bloch 球体上观察量子比特的衰减来演示这两种方法。
示例:量子比特衰减
计算量子比特衰变的泡利自旋算符期望值的代码如下所示。此代码在两个动画示例中都是通用的。
import numpy as np
import qutip
def qubit_integrate(w, theta, gamma1, gamma2, psi0, tlist):
# operators and the hamiltonian
sx = qutip.sigmax()
sy = qutip.sigmay()
sz = qutip.sigmaz()
sm = qutip.sigmam()
H = w * (np.cos(theta) * sz + np.sin(theta) * sx)
# collapse operators
c_op_list = []
n_th = 0.5 # temperature
rate = gamma1 * (n_th + 1)
if rate > 0.0: c_op_list.append(np.sqrt(rate) * sm)
rate = gamma1 * n_th
if rate > 0.0: c_op_list.append(np.sqrt(rate) * sm.dag())
rate = gamma2
if rate > 0.0: c_op_list.append(np.sqrt(rate) * sz)
# evolve and calculate expectation values
output = qutip.mesolve(H, psi0, tlist, c_op_list, [sx, sy, sz])
return output.expect[0], output.expect[1], output.expect[2]
## calculate the dynamics
w = 1.0 * 2 * np.pi # qubit angular frequency
theta = 0.2 * np.pi # qubit angle from sigma_z axis (toward sigma_x axis)
gamma1 = 0.5 # qubit relaxation rate
gamma2 = 0.2 # qubit dephasing rate
# initial state
a = 1.0
psi0 = (a*qutip.basis(2, 0) + (1-a)*qutip.basis(2, 1))/np.sqrt(a**2 + (1-a)**2)
tlist = np.linspace(0, 4, 250)
#expectation values for ploting
sx, sy, sz = qubit_integrate(w, theta, gamma1, gamma2, psi0, tlist)
生成动画图像
下面给出了一个在Python之外生成动画图像的示例:
import numpy as np
b = qutip.Bloch()
b.vector_color = ['r']
b.view = [-40, 30]
for i in range(len(sx)):
b.clear()
b.add_vectors([np.sin(theta), 0, np.cos(theta)])
b.add_points([sx[:i+1], sy[:i+1], sz[:i+1]])
b.save(dirc='temp') # saving images to temp directory in current working directory
使用FFmpeg(例如)生成动画相当简单:
ffmpeg -i temp/bloch_%01d.png bloch.mp4
直接生成动画
重要
直接从Matplotlib生成动画需要安装MEncoder或FFmpeg。
虽然在Linux上两者都可以使用,但在Mac上运行时最好选择FFmpeg。
如果使用macports,只需执行:sudo port install ffmpeg。
直接生成量子比特衰变的mp4视频的代码如下
from matplotlib import pyplot, animation
fig = pyplot.figure()
ax = fig.add_subplot(azim=-40, elev=30, projection="3d")
sphere = qutip.Bloch(axes=ax)
def animate(i):
sphere.clear()
sphere.add_vectors([np.sin(theta), 0, np.cos(theta)], ["r"])
sphere.add_points([sx[:i+1], sy[:i+1], sz[:i+1]])
sphere.render()
return ax
ani = animation.FuncAnimation(fig, animate, np.arange(len(sx)), blit=False, repeat=False)
ani.save('bloch_sphere.mp4', fps=20)
生成的电影可以在这里查看:bloch_decay.mp4