量子态和过程的可视化
可视化通常是量子力学系统模拟的重要补充。首先想到的可视化方法可能是绘制一些选定算符的期望值。但除此之外,例如可视化描述系统状态的状态向量或密度矩阵,或者状态如何随时间变化(见下文的过程层析成像),通常也能提供有益的见解。在本节中,我们将演示如何使用QuTiP和matplotlib进行几种类型的可视化,这些可视化通常可以提供对量子系统的额外理解。
Fock基概率分布
在量子力学中,概率分布起着重要作用,与统计学中一样,从概率分布计算出的期望值并不能揭示全部信息。例如,考虑一个具有哈密顿量 \(H = \hbar\omega a^\dagger a\) 的量子谐振子模式,其状态由其密度矩阵 \(\rho\) 描述,并且平均占据两个光子,\(\mathrm{Tr}[\rho a^\dagger a] = 2\)。根据这些信息,我们无法判断振子是否处于福克态、热态、相干态等。通过在福克态基础上可视化光子分布,可以获得关于底层状态的重要线索。
一种可视化概率分布的便捷方法是使用直方图。 考虑以下基于数字的概率分布的直方图可视化, 它可以从密度矩阵的对角线获得, 适用于几种可能的振荡器状态,平均占据两个光子。
首先我们生成相干态、热态和福克态的密度矩阵。
N = 20
rho_coherent = coherent_dm(N, np.sqrt(2))
rho_thermal = thermal_dm(N, 2)
rho_fock = fock_dm(N, 2)
接下来,我们绘制密度矩阵对角线的直方图:
fig, axes = plt.subplots(1, 3, figsize=(12,3))
bar0 = axes[0].bar(np.arange(0, N)-.5, rho_coherent.diag())
lbl0 = axes[0].set_title("Coherent state")
lim0 = axes[0].set_xlim([-.5, N])
bar1 = axes[1].bar(np.arange(0, N)-.5, rho_thermal.diag())
lbl1 = axes[1].set_title("Thermal state")
lim1 = axes[1].set_xlim([-.5, N])
bar2 = axes[2].bar(np.arange(0, N)-.5, rho_fock.diag())
lbl2 = axes[2].set_title("Fock state")
lim2 = axes[2].set_xlim([-.5, N])
plt.show()
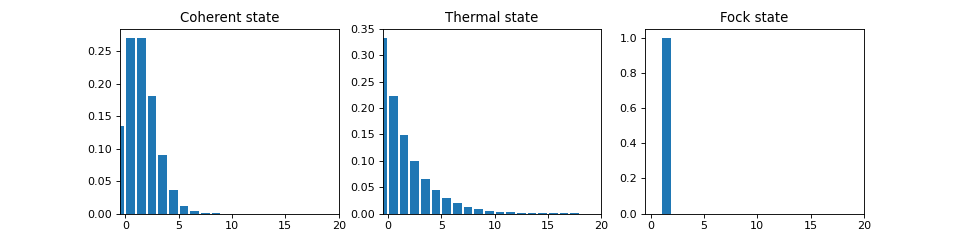
所有这些状态对应于平均两个光子,但通过在Fock基中可视化光子分布,这些状态之间的差异很容易被理解。
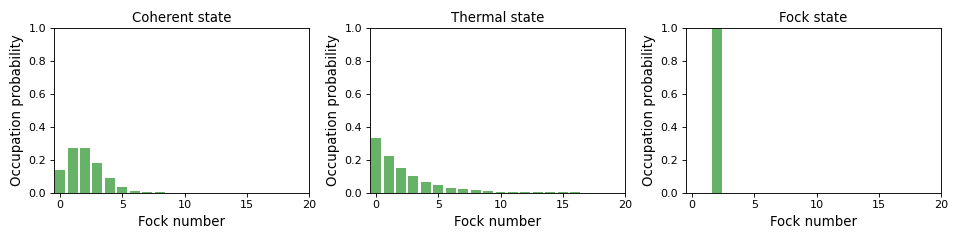
经常需要以上述方式可视化Fock分布,因此QuTiP提供了一个方便的函数来实现这一点,参见
qutip.visualization.plot_fock_distribution,以及以下示例:
fig, axes = plt.subplots(1, 3, figsize=(12,3))
fig, axes[0] = plot_fock_distribution(rho_coherent, fig=fig, ax=axes[0]);
axes[0].set_title('Coherent state')
fig, axes[1] = plot_fock_distribution(rho_thermal, fig=fig, ax=axes[1]);
axes[1].set_title('Thermal state')
fig, axes[2] = plot_fock_distribution(rho_fock, fig=fig, ax=axes[2]);
axes[2].set_title('Fock state')
fig.tight_layout()
plt.show()
准概率分布
在数字(Fock)基中的概率分布仅描述了一组离散状态的占据概率。对于谐波模式,更完整的相空间概率分布类函数是Wigner和Husumi Q函数,它们是对量子态的完整描述(等同于密度矩阵)。这些被称为准分布函数,因为与真实的概率分布函数不同,它们可以是负的。除了是对状态的更完整描述(与仅绘制占据概率相比),这些分布也非常适合展示量子态是否是量子力学的,因为例如负的Wigner函数是状态明显非经典的一个明确指标。
维格纳函数
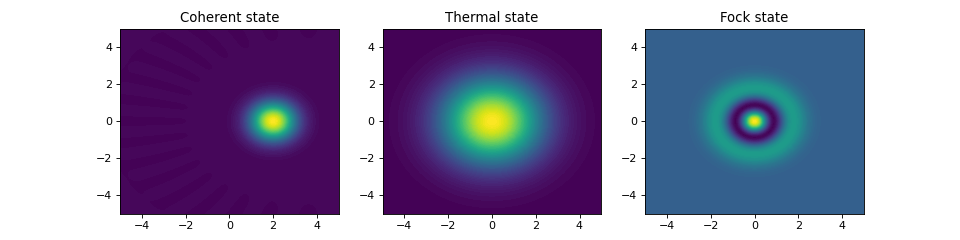
在QuTiP中,可以使用函数qutip.wigner.wigner来计算谐波模式的Wigner函数。它接受一个ket或密度矩阵作为输入,以及定义相空间坐标范围(在x-y平面中)的数组。在以下示例中,计算并绘制了与前一节相同的三种状态的Wigner函数。
xvec = np.linspace(-5,5,200)
W_coherent = wigner(rho_coherent, xvec, xvec)
W_thermal = wigner(rho_thermal, xvec, xvec)
W_fock = wigner(rho_fock, xvec, xvec)
# plot the results
fig, axes = plt.subplots(1, 3, figsize=(12,3))
cont0 = axes[0].contourf(xvec, xvec, W_coherent, 100)
lbl0 = axes[0].set_title("Coherent state")
cont1 = axes[1].contourf(xvec, xvec, W_thermal, 100)
lbl1 = axes[1].set_title("Thermal state")
cont0 = axes[2].contourf(xvec, xvec, W_fock, 100)
lbl2 = axes[2].set_title("Fock state")
plt.show()
自定义颜色映射
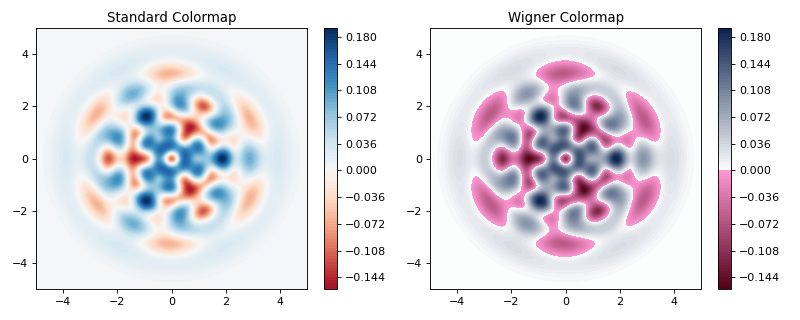
绘制Wigner函数的主要目的是展示基础状态是非经典的,这通过Wigner函数中的负值来指示。因此,在图中突出这些负值对于分析和发布目的都是有益的。不幸的是,Matplotlib(或任何其他绘图软件)中使用的所有颜色方案都是线性颜色映射,其中小的负值往往与零值附近的颜色相同,因此被隐藏。为了解决这个问题,QuTiP包含了一个非线性颜色映射函数qutip.matplotlib_utilities.wigner_cmap,它将所有负值着色为与正值或零值不同的颜色。以下是如何在您的Wigner图中使用此函数的演示:
import matplotlib as mpl
from matplotlib import cm
psi = (basis(10, 0) + basis(10, 3) + basis(10, 9)).unit()
xvec = np.linspace(-5, 5, 500)
W = wigner(psi, xvec, xvec)
wmap = wigner_cmap(W) # Generate Wigner colormap
nrm = mpl.colors.Normalize(-W.max(), W.max())
fig, axes = plt.subplots(1, 2, figsize=(10, 4))
plt1 = axes[0].contourf(xvec, xvec, W, 100, cmap=cm.RdBu, norm=nrm)
axes[0].set_title("Standard Colormap");
cb1 = fig.colorbar(plt1, ax=axes[0])
plt2 = axes[1].contourf(xvec, xvec, W, 100, cmap=wmap) # Apply Wigner colormap
axes[1].set_title("Wigner Colormap");
cb2 = fig.colorbar(plt2, ax=axes[1])
fig.tight_layout()
plt.show()
Husimi Q函数
Husimi Q 函数与 Wigner 函数一样,是谐波模式的准概率分布。它被定义为
其中 \(\left|\alpha\right>\) 是一个相干态,且
\(\alpha = x + iy\)。在 QuTiP 中,可以使用函数 qfunc 来计算给定态矢或密度矩阵的 Husimi Q 函数,如下所示。
Q_coherent = qfunc(rho_coherent, xvec, xvec)
Q_thermal = qfunc(rho_thermal, xvec, xvec)
Q_fock = qfunc(rho_fock, xvec, xvec)
fig, axes = plt.subplots(1, 3, figsize=(12,3))
cont0 = axes[0].contourf(xvec, xvec, Q_coherent, 100)
lbl0 = axes[0].set_title("Coherent state")
cont1 = axes[1].contourf(xvec, xvec, Q_thermal, 100)
lbl1 = axes[1].set_title("Thermal state")
cont0 = axes[2].contourf(xvec, xvec, Q_fock, 100)
lbl2 = axes[2].set_title("Fock state")
plt.show()
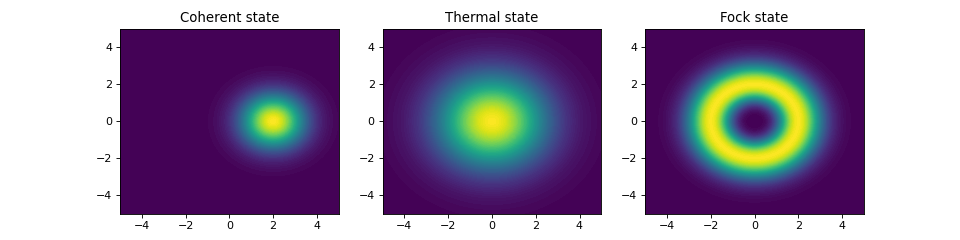
如果你需要为许多具有相同相空间坐标的状态计算Q函数,使用QFunc类会更高效。这存储了各种中间结果,与在循环中调用qfunc相比,可以实现数量级的改进。
xs = np.linspace(-1, 1, 101)
qfunc_calculator = qutip.QFunc(xs, xs)
q_state1 = qfunc_calculator(qutip.rand_dm(5))
q_state2 = qfunc_calculator(qutip.rand_ket(100))
可视化操作符
有时,直接可视化算子的底层矩阵表示也可能很有用。例如,密度矩阵是一个算子,其元素可以提供有关其所表示状态的见解,但人们可能也对绘制哈密顿量的矩阵感兴趣,以检查各种元素的结构和相对重要性。
QuTiP 提供了一些函数,用于快速可视化矩阵数据,形式包括直方图,qutip.visualization.matrix_histogram 和作为加权正方形的 Hinton 图,qutip.visualization.hinton。这些函数以 Qobj 作为第一个参数,并且可以接受可选参数,例如设置轴标签和图形标题(详见函数的文档)。
例如,为了说明qutip.visualization.matrix_histogram的使用,让我们可视化Jaynes-Cummings哈密顿量:
N = 5
a = tensor(destroy(N), qeye(2))
b = tensor(qeye(N), destroy(2))
sx = tensor(qeye(N), sigmax())
H = a.dag() * a + sx - 0.5 * (a * b.dag() + a.dag() * b)
# visualize H
lbls_list = [[str(d) for d in range(N)], ["u", "d"]]
xlabels = []
for inds in tomography._index_permutations([len(lbls) for lbls in lbls_list]):
xlabels.append("".join([lbls_list[k][inds[k]] for k in range(len(lbls_list))]))
fig, ax = matrix_histogram(H, xlabels, xlabels, limits=[-4,4])
ax.view_init(azim=-55, elev=45)
plt.show()
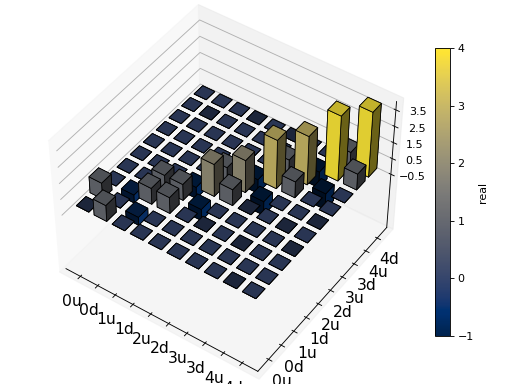
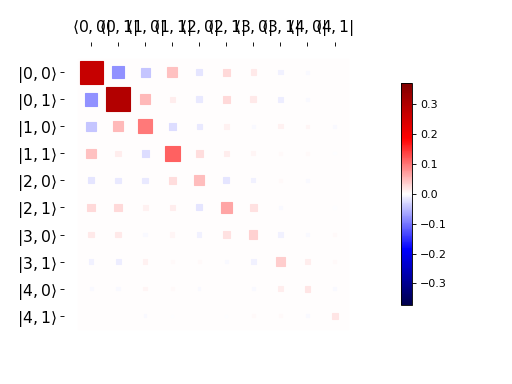
同样地,我们可以使用函数 qutip.visualization.hinton,它用于可视化相应的稳态密度矩阵:
rho_ss = steadystate(H, [np.sqrt(0.1) * a, np.sqrt(0.4) * b.dag()])
hinton(rho_ss)
plt.show()
量子过程层析成像
量子过程层析成像(QPT)是一种用于表征涉及少量量子比特的量子门实验实现的有用技术。它也可以作为一种有用的理论工具,可以深入了解过程如何转换状态,并且可以用于研究噪声或其他缺陷如何使门退化。虽然保真度或距离度量可以给出一个单一的数字,表明门与理想状态的差距,但量子过程层析成像分析可以提供关于各种缺陷引入的错误的详细信息。
这个想法是为量子过程(例如量子门)构建一个变换矩阵,该矩阵描述了系统的密度矩阵如何通过该过程进行变换。然后,我们可以在一些算子基中分解这个变换,这些算子基代表了输入状态的明确定义且易于解释的变换。
要了解这是如何工作的(更多详情请参见例如 [Moh08]),考虑一个由量子映射 \(\epsilon(\rho_{\rm in}) = \rho_{\rm out}\) 描述的过程,它可以写成
其中 \(N\) 是系统的状态数(即 \(\rho\) 由一个 \([N\times N]\) 矩阵表示)。给定我们选择的正交算子基 \(\{B_i\}_i^{N^2}\),它满足 \({\rm Tr}[B_i^\dagger B_j] = N\delta_{ij}\),我们可以将映射写为
其中 \(\chi_{mn} = \sum_{ij} b_{im}b_{jn}^*\) 和 \(A_i = \sum_{m} b_{im}B_{m}\)。这里,矩阵 \(\chi\) 是我们所寻找的变换矩阵,因为它描述了 \(B_m \rho_{\rm in} B_n^\dagger\) 对 \(\rho_{\rm out}\) 的贡献程度。
在量子过程的数值模拟中,我们通常无法以方程 (1) 的形式访问量子映射。相反,我们通常能做的是计算密度矩阵的超算符形式的传播子 \(U\),例如使用 QuTiP 函数 qutip.propagator.propagator。然后我们可以写成
其中 \(\tilde{\rho}\) 是密度矩阵 \(\rho\) 的向量表示。如果我们将方程 (2) 也写成超算符形式,我们得到
所以我们可以识别
现在这是一个关于\(\chi\)中\(N^2 \times N^2\)元素的线性方程组。我们可以通过将\(\chi\)和超算子传播器写成\([N^4]\)向量来解决它,同样将超算子乘积\(\tilde{B}_m\tilde{B}_n^\dagger\)写成一个\([N^4\times N^4]\)矩阵\(M\):
使用解决方案
请注意,要使用此方法获得\(\chi\),我们必须构造一个大小为系统超算符大小平方的矩阵\(M\)。显然,随着系统规模的增加,这种方法扩展得非常糟糕,但对于小系统(例如由少量耦合量子比特组成的系统)来说,这种方法仍然非常有用。
在QuTiP中的实现
在QuTiP中,上述过程在函数qutip.tomography.qpt中实现,该函数返回给定密度矩阵传播子的\(\chi\)矩阵。
为了说明如何使用此函数,让我们考虑两个量子比特的SWAP门。在QuTiP中,函数swap生成状态ket的幺正变换:
from qutip.core.gates import swap
U_psi = swap()
为了能够使用这个单一变换矩阵作为函数 qutip.tomography.qpt 的输入,我们首先需要将其转换为相应密度矩阵的变换矩阵:
U_rho = spre(U_psi) * spost(U_psi.dag())
接下来,我们构建一个操作符列表,这些操作符以每个复合系统的操作符列表形式定义了基\(\{B_i\}\)。同时,我们还构建了一个对应的标签列表,这些标签将在绘制\(\chi\)矩阵时使用。
op_basis = [[qeye(2), sigmax(), sigmay(), sigmaz()]] * 2
op_label = [["i", "x", "y", "z"]] * 2
我们现在准备使用qutip.tomography.qpt计算\(\chi\),并使用qutip.tomography.qpt_plot_combined进行绘图。
chi = qpt(U_rho, op_basis)
fig = qpt_plot_combined(chi, op_label, r'SWAP')
plt.show()
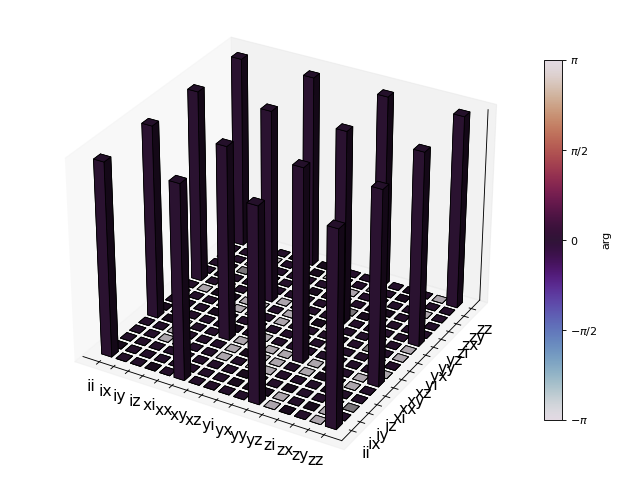
对于一个稍微高级一点的例子,其中密度矩阵传播器是通过使用函数propagator从其哈密顿量和崩溃算符定义的系统的动力学中计算出来的,请参阅QuTiP网站教程部分中的笔记本“时间依赖的主方程:Landau-Zener跃迁”。