量子最优控制
介绍
在量子控制中,我们致力于准备一些特定的状态,实现一些状态到状态的转移,或者在量子系统上实现一些变换(或门)。对于一个给定的量子系统,总会有一些影响动力学的因素是我们无法控制的。例如,系统元素之间的相互作用或捕获系统所需的磁场。然而,可能有方法以受控的方式影响动力学,例如相互作用激光场的电分量的时间变化幅度。因此,这引出了几个问题;给定一个具有已知时间无关动力学生成器(称为漂移动力学生成器)的特定量子系统,以及一组外部可控场,其相互作用可以通过控制动力学生成器来描述:
我们可以实现哪些状态或转换(如果有的话)?
实现这一目标所需的控制脉冲形状是什么?
这些问题被作为可控性和量子最优控制 [dAless08]来讨论。可控性问题的答案由动力学生成元的可交换性决定,并被形式化为李代数秩准则,并在[dAless08]中详细讨论。第二个问题的解决方案可以通过最优控制算法或控制脉冲优化来确定。
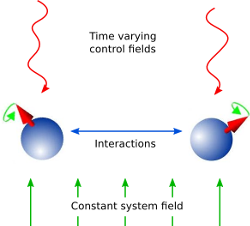
展示量子控制原理的示意图。
量子控制有许多应用,包括核磁共振、量子计量学、化学反应控制和量子信息处理。
为了解释这些算法背后的物理原理,我们首先将只考虑有限维的封闭量子系统。
封闭量子系统
在封闭量子系统中,状态可以用kets表示,这些状态上的变换是幺正算子。动力学生成器是哈密顿量。系统的组合哈密顿量由以下公式给出:
其中 \(H_0\) 是漂移哈密顿量,而 \(H_j\) 是控制哈密顿量。\(u_j\) 是特定控制的时间变化幅度函数。
系统的动力学由Schrödingers equation控制。
注意我们在整个过程中使用单位\(\hbar=1\)。薛定谔方程的解的形式为:
其中 \(\psi_0\) 是系统在 \(t=0\) 时的状态,\(U(t)\) 是包含状态的希尔伯特空间上的一个幺正算子。\(U(t)\) 是 薛定谔算子方程 的解
我们可以使用最优控制算法来确定一组\(u_j\),这将驱动我们的系统从\(\ket{\psi_0}\)到\(\ket{\psi_1}\),这是状态到状态的转移,或者将系统从某个任意状态驱动到给定状态\(\ket{\psi_1}\),这是状态准备,或者实现某个幺正变换\(U_{target}\),称为门合成。后者在量子计算中最为重要。
GRAPE算法
GRadient Ascent Pulse Engineering 首次在 [NKanej] 中提出。对于时间依赖的哈密顿量的薛定谔方程的解通常无法通过解析方法获得。因此,对脉冲幅度进行了分段常数近似。系统演化的时间 \(T\) 被分成 \(M\) 个时间槽(通常这些时间槽的持续时间相等),在此期间控制幅度被假定为保持不变。然后,组合哈密顿量可以近似为:
其中 \(k\) 是时间槽索引,\(j\) 是控制索引,\(N\) 是控制的数量。因此 \(t_k\) 是时间槽开始时的演化时间,\(u_{jk}\) 是控制 \(j\) 在整个时间槽 \(k\) 中的振幅。时间槽内的时间演化算子或传播子可以计算为:
其中 \(\Delta t_k\) 是时间段的持续时间。直到(并包括)任何时间段 \(k\)(包括完整的演化 \(k=M\))的演化可以计算为
如果目标是状态到状态的转移,那么 \(X_0=\ket{\psi_0}\) 和目标 \(X_{targ}=\ket{\psi_1}\),对于门合成 \(X_0 = U(0) = \mathbb{1}\) 和目标 \(X_{targ}=U_{targ}\)。
一个品质因数或保真度是基于时间段内的控制幅度来衡量演化与目标的接近程度。对于酉系统,典型的品质因数是演化与目标的归一化重叠。
其中 \(d\) 是系统的维度。在这个性能指标中,取绝对值是为了忽略全局相位的任何差异,且 \(0 \le f \le 1\)。通常,保真度误差(或不保真度)更有用,在这种情况下定义为 \(\varepsilon = 1 - f_{PSU}\)。还有许多其他可能的目标,因此也有许多其他性能指标。
由于现在有\(N \times M\)个变量(即\(u_{jk}\))和一个需要最小化的参数\(\varepsilon\),问题就变成了一个有限的多变量优化问题,对于这类问题有许多成熟的方法,通常被称为“爬山”方法。其中最容易理解的是最陡上升(或下降)法。计算(或近似)所有变量的保真度梯度,并在变量空间中朝着最陡上升(或下降)方向迈出一步。这种方法是一阶梯度法。在二维情况下,这描述了一种通过朝着地面上升最快的方向爬山的方法。这个类比也清楚地说明了多变量优化中的一个主要挑战,即所有方法都有陷入局部最大值的倾向。很难确定是否找到了全局最大值——局部峰值很可能不是该地区的最高山峰。在量子最优控制中,我们通常可以定义一个下界为零的不保真度。然后我们可以寻求最小化不保真度(从现在开始我们只考虑优化不保真度最小值)。这意味着当不保真度达到零(达到足够的精度)时,我们可以终止任何脉冲优化。然而,这只有在完全可控的系统中才有可能;否则很难(如果不是不可能)知道是否达到了可能的最小不保真度。在爬山类比中,步长大致固定为一步,然而在计算中必须选择步长。显然,在达到最小值所需的步数(或迭代次数)与可能跳过最小值之间存在权衡。在实践中,很难确定一个高效且有效的步长。
关于变量的不保真度的二阶微分可以用来近似局部景观为抛物线。这样,可以一步(或跳跃)到如果它是抛物线时最小值所在的位置。这通常大大减少了迭代次数,并且不需要猜测步长。所有二阶微分都明确计算的方法称为牛顿-拉弗森方法。然而,计算二阶微分(海森矩阵)可能在计算上非常昂贵,因此有一类方法称为拟牛顿方法,它们基于连续迭代来近似海森矩阵。其中最流行的(在量子最优控制中)是Broyden–Fletcher–Goldfarb–Shanno算法(BFGS)。QuTiP Qtrl GRAPE实现中的默认方法是Scipy中的L-BFGS-B方法,它是对[Byrd95]中描述的实现的封装。这种有限内存和有界方法不需要存储整个海森矩阵,从而减少了所需的计算机内存,并允许为变量值设置界限,考虑到这些是场振幅,这通常是物理的。
如果梯度可以精确计算而不是近似计算,脉冲优化通常会更加高效。对于简单的保真度度量,如\(f_{PSU}\),这是可能的。首先,计算每个时间段相对于控制幅度的传播器梯度。对于具有单一动力学的封闭系统,使用基于特征分解的方法,这种方法效率高,因为它也用于传播器计算(以指数化组合哈密顿量)。更一般地(例如开放系统和辛动力学),使用Frechet导数(或增广矩阵)方法,这在[Flo12]中有描述。对于其他优化目标,可能无法计算解析梯度。在这些情况下,有必要近似梯度,但这可能非常昂贵,并可能导致其他算法优于GRAPE。
CRAB算法
已经证明[Lloyd14],量子最优控制问题的维度是时间多项式可达状态流形维度的多项式函数,当允许有限的控制精度和演化时间时。你可以将其视为脉冲的信息内容(作为唯一有效的输入)非常有限,例如,脉冲可以在不丢失目标的情况下压缩到几个字节。
这是Chopped RAndom Basis (CRAB)算法 [Doria11], [Caneva11]发挥作用的地方:由于脉冲复杂度通常 非常低,通过引入一个物理动机的函数基来构建脉冲,将最优控制问题转化为少量 参数搜索就足够了。与准确模拟量子动力学所需的时间切片数量(通常等于基于梯度的 算法的基维度)相比,这个数量级要低得多,使得CRAB能够 在现实的实验约束下高效地优化平滑脉冲。需要指出的是,CRAB并不对使用的基函数 提出任何建议。必须仔细考虑选择基函数,考虑到系统的先验知识(如对称性、尺度大小等) 和解决方案(例如符号、平滑性、bang-bang行为、 奇点、最大偏移或变化率等)。通过这样做,该 算法允许原生集成实验约束,如允许的最大频率、 最大振幅、脉冲的平滑上升和下降等。此外,如果有初始猜测, 可以(但不是必须)包含它们以加速收敛。
正如GRAPE段落中提到的,CRAB也可能由于算法设计而产生局部最小值。然而,最近为CRAB引入了一个“修饰”版本[Rach15],它允许逃离局部最小值。
对于一些控制目标和/或动态量子描述,可能无法推导出成本函数相对于每个时间片的梯度,或者这样做在计算上是昂贵的。同样的情况也可能适用于共态的必要(反向)传播。所有这些麻烦在CRAB中都不会发生,因为这些元素在这里没有被使用。相反,CRAB将时间演化视为一个黑箱,其中脉冲作为输入,成本(例如不保真度)值将作为输出返回。这个概念还允许在闭环实验环境中直接集成,其中初步的开环优化以及最终的采用和集成到实验室(以考虑建模错误、实验系统噪声等)都可以使用这个算法一次性完成。
QuTiP中的最优量子控制
qutip的量子控制部分已移至其自己的项目。
之前可用的实现现在位于qutip-qtrl模块中。如果安装了qutip-qtrl包,它也可以以qutip.control的名称导入,以便于将为QuTiP 4开发的代码移植到QuTiP 5。
一个具有升级功能的新接口正在qutip-qoc中开发。
请尝试这些模块。